【数学+枚举】OpenJ_POJ - C17J Pairs

https://vjudge.net/contest/171652#problem/J

【题意】

问有多少个正整数对(x,y)，使得存在正整数p,q满足

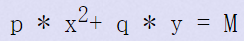
1 <= T <= 15

1 <= M <= 800,000

【思路】

• M最多8e5，所以考虑枚举x,只有1e3个
• 对于某个x,有多少对(x,y)其实就是看m-p*x*x有多少个不同的因子（需要去重）
• 我们可以预处理1~8e5的每个数的所有因子（mlogm）
• 分别枚举x,p,对所有m-p*x*x的因子去重，因为最大是因子8e5，所以可以开一个数组去重
• 总的时间复杂度就是O(mlogm)+O(m*240)=O(mlogm)
• m+m/4+m/9......是线性的，所有数的因子最多是240个左右

【Accepted】

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<string>
 #include<cmath>
 #include<algorithm>
 #include<queue>
 #include<set>
 #include<vector>
 using namespace std;
 typedef long long ll;
 const ll mod=1e9+;
 const int maxn=8e5+;
 set<int> s[maxn];
 set<int>::iterator it;
 vector<int> v[maxn];
 bool vis[maxn];
 int n;
 void init()
 {

     for(int i=;i<maxn;i++)
     {
         for(int j=i;j<maxn;j+=i)
         {
             v[j].push_back(i);
          }
     }
     int mmax=;
     for(int i=;i<maxn;i++)
     {
         int sz=v[i].size();
         mmax=max(mmax,sz);
     }
     cout<<mmax<<endl;
 }
 int main()
 {
     init();
     int T;
     scanf("%d",&T);
     while(T--)
     {

         scanf("%d",&n);
         int cnt=;
         for(int i=;i<n;i++)
         {
             memset(vis,false,sizeof(vis));
             int x=i*i;
             if(x>=n) break;
             for(int j=;j<n;j++)
             {
                 if(x*j>=n) break;
                 int y=n-x*j;
                 for(int k=;k<v[y].size();k++)
                 {
                     if(!vis[v[y][k]])
                     {
                         vis[v[y][k]]=true;
                         cnt++;
                     }
                 }
             }
         }
         printf("%d\n",cnt);
     }
     return ;
 }

【教训】

一开始T了是因为，为了去重所有容器都用了set,这样复杂度就带了logn

而vector的push_back是O(1)的