[JSOI2007] 祖玛 (区间DP)

题目描述

这是一个流行在Jsoi的游戏，名称为祖玛。

精致细腻的背景，外加神秘的印加音乐衬托，彷佛置身在古老的国度里面，进行一个神秘的游戏——这就是著名的祖玛游戏。祖玛游戏的主角是一只石青蛙，石青蛙会吐出各种颜色的珠子，珠子造型美丽，并且有着神秘的色彩。

环绕着石青蛙的是载着珠子的轨道，各种颜色的珠子会沿着轨道往前滑动，石青蛙必需遏止珠子们滚进去轨道终点的洞里头，如何减少珠子呢？就得要靠石青蛙吐出的珠子与轨道上的珠子相结合，颜色相同者即可以消失得分！直到轨道上的珠子通通都被清干净为止。或许你并不了解祖玛游戏。没关系。这里我们介绍一个简单版本的祖玛游戏规则。一条通道中有一些玻璃珠，每个珠子有各自的颜色，如图1所示。玩家可以做的是选择一种颜色的珠子（注意：颜色可以任选，这与真实游戏是不同的）射入某个位置。

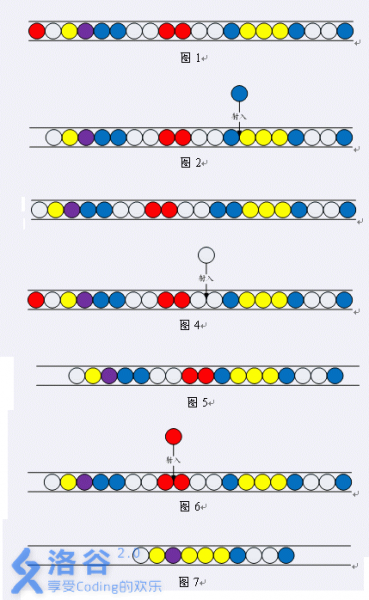
图1 图2中玩家选择一颗蓝色珠子，射入图示的位置，于是得到一个图3的局面。

图2 图3 当玩家射入一颗珠子后，如果射入的珠子与其他珠子组成了三颗以上连续相同颜色的珠子，这些珠子就会消失。例如，将一颗白色珠子射入图4中的位置，就会产生三颗颜色相同的白色珠子。这三颗珠子就会消失，于是得到图5的局面。

图4 图5 需要注意的一点是，图4中的三颗连续的黄色珠子不会消失，因为并没有珠子射入其中。珠子的消失还会产生连锁反应。当一串连续相同颜色的珠子消失后，如果消失位置左右的珠子颜色相同，并且长度大于2，则可以继续消失。例如，图6中，射入一颗红色珠子后，产生了三颗连续的红色珠子。当红色珠子消失后，它左右都是白色的珠子，并且一共有四颗，于是白色珠子也消失了。之后，消失位置的左右都是蓝色珠子，共有三颗，于是蓝色珠子也消失。最终得到图7的状态。注意，图7中的三颗黄色珠子不会消失，因为蓝色珠子消失的位置一边是紫色珠子，另一边是黄色珠子，颜色不同。

图6 图7 除了上述的情况，没有其他的方法可以消去珠子。现在，我们有一排珠子，需要你去消除。对于每一轮，你可以自由选择不同颜色的珠子，射入任意的位置。你的任务是射出最少的珠子，将全部珠子消去。

Solution

这是本蒟蒻博主自己想出来的第一道省选DP.想了一整天啊　QAQ...

这道题的主要难度是对题意的理解,即要找出这个题目的最关键特点.

通过题面可以知道,在一个序列中,如果有连续的一段颜色,那么无论怎么样,在最终合并的时候,它们都不会被分开的.

然后又鉴于它颜色的种类可能很大,开不下那么大的数组,所以我们就在DP前需要进行一次预处理.

一个是把颜色离散(这个其实也没必要),第二个就是要把所有连续的颜色相同的点都处理在一起,形成一个新的序列.

同时在这个新的序列中我们要记录每一个新的元素包含的节点个数,这是为了满足游戏规则里的至少要三个才能合并的条件.

然后这之后就是一个较为简单的区间DP

枚举i j 和断点 k.

然后这个时候有两种情况可以合并：

1. 直接 i -> k 和 k+1 -> j 两段合并.

2. 中间的先合并,然后两边合并,连锁反应.

Ps: 原题里有一个比较坑的数据点在讨论版里面. 所以有特判.

代码

#include<bits/stdc++.h>

using namespace std;

const int maxn=;

int n,len,f[maxn][maxn],pd[maxn];

int c[maxn],num,a[maxn],col[maxn],newt[maxn];  

void pre()

{

    sort(a+,a+n+);

    for(int i=;i<=n;)

    {

        int xx=a[i],flag=; col[++num]=xx;

        while(a[i+flag]==xx) flag++;

        i+=flag;

    }

    for(int i=;i<=n;i++)

    for(int j=;j<=num;j++)

    if(c[i]==col[j])

    {c[i]=j;break;}

    for(int i=;i<=n;)

    {

        int xx=c[i]; int flag=;

        while(c[i+flag]==xx) flag++;

        newt[++len]=xx; pd[len]=flag;

        f[len][len]=(flag!=)?:;   i+=flag;

    }

}

int main()

{

    scanf("%d",&n);

    if(n==){cout<<<<endl;return ;}

    for(int i=;i<=n;i++)

    scanf("%d",&a[i]),c[i]=a[i];

    memset(f,0x7f,sizeof(f));

    pre();

    for (int i=;i<=len-;++i)

    for (int j=;j<=len-i;++j)

    {

            if (newt[j]==newt[j+i])

                if (i==)  f[j][j+i]=pd[j]+pd[j+i]>=?:;

                else f[j][j+i]=f[j+][j+i-]+(pd[j]+pd[j+i]>=?:);

            for (int k=j;k<j+i;++k)

                f[j][j+i]=min(f[j][j+i],f[j][k]+f[k+][j+i]);

       }

    cout<<f[][len]<<endl;

}