[COCI2006-2007 Contest#3] BICIKLI

不难的一道题，就是码的时候出了点问题，看了其他巨佬的题解才发现问题所在...

题目大意：

给定一个有向图，n个点，m条边。请问，1号点到2号点有多少条路径？如果有无限多条，输出inf，如果有限，输出答案模1e9的余数。

首先是0的情况：

　　不存在1~2的路径，即图不一定联通（不这样特判也可以，但是常数会小一点）

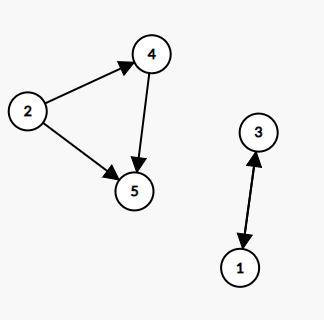
其次是inf的情况：

　　如果在1~2的某条路径中存在某个点属于某个强连通分量，那么这条路径就可以在这个强连通分量里无限走下去，答案就是inf

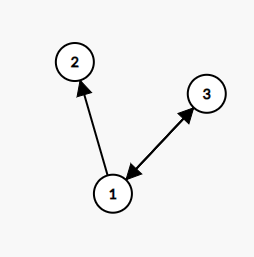
一般情况:

　　如果这条路径不属于第二种情况，那就考虑计数吧...

　　我们可以用一个dp数组计数，然后乱搞BFS即可，不用考虑是否vis，因为排除了第二种情况后显然是不会过度访问（RE）的

　　同时我们可以记录每一个节点的入度个数，在最后BFS,DP的时候，根据入度可以减少判断很多情况

同时：一个小问题：在考虑情况2的时候，我们需要建立反向边，以便判断1,2可达性（刚开始想当然了这个没判）

 #pragma GCC optimize("Ofast")
 #pragma GCC optimize(3)
 #include<cstdio>
 #include<iostream>
 #include<cstring>
 #include<queue>
 #define ha 1000000000
 using namespace std;
 inline int read(){
     int ans=,f=;char chr=getchar();
     while(!isdigit(chr)){if(chr=='-') f=-;chr=getchar();}
     while(isdigit(chr)){ans=(ans<<)+(ans<<)+chr-;chr=getchar();}
     return ans*f;
 }void write(int x){
     if(x<) putchar('-'),x=-x;
     if(x>) write(x/);
     putchar(x%+'');
 }const int M=1e5+;
 int head[M],head1[M],ver1[M],nxt1[M],ver[M],nxt[M],tot,n,m,vis1[M],vis2[M],dfn[M],low[M],ins[M],sta[M],top,t,col,color[M],cnt[M],tot1,dp[M],in[M];
 inline void add(int x,int y){ver[++tot]=y;nxt[tot]=head[x];head[x]=tot;}
 inline void add1(int x,int y){ver1[++tot1]=y;nxt1[tot1]=head1[x];head1[x]=tot1;}
 void dfs1(int x){for(int i=head[x];i;i=nxt[i])if(in[ver[i]]++,!vis1[ver[i]])dfs1(ver[vis1[ver[i]]=,i]);}
 void dfs2(int x){for(int i=head1[x];i;i=nxt1[i])if(!vis2[ver1[i]])dfs2(ver1[vis2[ver1[i]]=,i]);}
 inline bool check_LT(){vis2[]=,dfs2();if(vis1[vis1[]=,dfs1(),]) return ;return ;}
 void Tarjan(int x){
     sta[top++]=x;low[x]=dfn[x]=++t;ins[x]=;
     for(register int i=head[x];i;i=nxt[i])
         if(ins[ver[i]]==) low[x]=min(low[x],dfn[ver[i]]);
         else if(ins[ver[i]]==) low[x]=min(low[Tarjan(ver[i]),x],low[ver[i]]);
     low[x]==dfn[x]?++col:col;
     if(low[x]==dfn[x])do{--top,color[sta[top]]=col,ins[sta[top]]=-,++cnt[col];}while(sta[top]!=x);
 }queue<int> q;
 void BFS(){
     q.push();dp[]=;
     while(!q.empty()){
         int x=q.front();q.pop();
         for(register int i=head[x];i;i=nxt[i]){
             if(!vis1[ver[i]]) continue;
             dp[ver[i]]=(dp[ver[i]]+dp[x])%ha;
             if(!--in[ver[i]])    q.push(ver[i]);
         }
     }
 }
 int main(){
     n=read(),m=read();
     for(register int i=,x,y;i<=m;++i) x=read(),y=read(),add(x,y),add1(y,x);
     if(check_LT()){return puts(""),;}
     for(register int i=;i<=n;++i) if(!dfn[i]) Tarjan(i);
     for(register int i=;i<=n;++i)
         if(vis1[i]&&vis2[i]&&cnt[color[i]]>=)
             return puts("inf"),;
     return BFS(),write(dp[]),;
 }