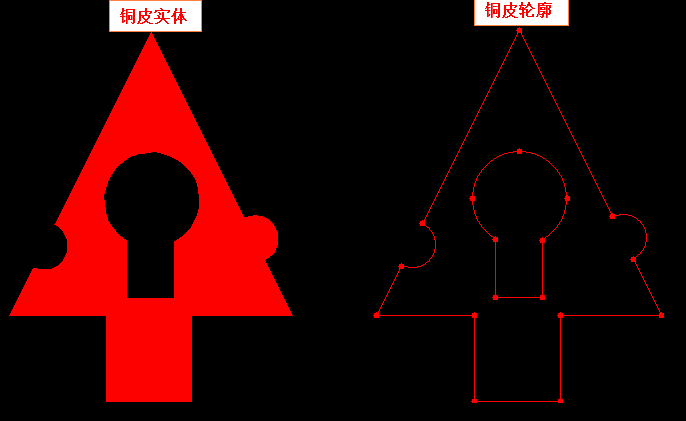
PCB 线路铜皮面积(残铜率)计算的实现方法
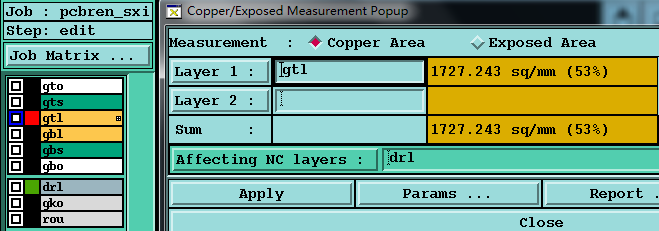
一个多月没更新博客园了，这里继续分享关于PCB工程相关一些知识，做过PCB工程都知道用使用genesis或incam是可以非常方便的计算得到铜皮面积这个参数【下图】，但实际这个软件是通过什么算法计算出铜面积的呢，这个我们不得而知，但接下来这里介绍一种可以将【线路铜皮面积(残铜率)】计算得出来的方法.
1.铜面积公式
公式=【铜面的多边形面积】+【铜的多边形周长*铜厚】-【孔的底面积】+【孔的圆柱面积】
注:看看计算公式是多么简单呀,是吧。下面重点讲【铜面的多边形面积】参数计算方法，因为其它参数过于简单就不写了
2.铜面积参数
1.表面铜面积【铜面的多边形面积】
2.表面横截面积【铜的多边形周长*铜厚】
3.有铜孔孔径面积【孔的底面积】
4.有铜孔孔壁面积【孔的圆柱面积】
【铜面的多边形面积】计算公式用 Shoelace公式 【鞋带公式】,此公式可以计算任意凸凹多边形,刚好是满足计算需求的，但对于PCB 铜皮(Surface)来说,铜皮点节点存在弧节点,直接用此公式计算当然不行啦，需要改造一下才行的。接一来用两种方法(丢失精度与精度)实现计算【铜面的多边形面积】
1.Shoelace公式 【鞋带公式】定义
公式图片来源引用 https://www.cnblogs.com/Khan-Sadas/p/10135717.html
定义：所述鞋带式或鞋带算法（也称为高斯的面积公式和测量员的式）是一种数学算法，以确定区域一个的简单多边形，其顶点由它们的描述笛卡尔坐标中的平面。用户交叉倍增相应的坐标，找到包含多边形的区域，并从周围的多边形中减去它，以找到其中的多边形区域。它被称为鞋带配方，因为构成多边形的坐标不断交叉倍增，就像绑鞋带一样。它有时也被称为鞋带方法
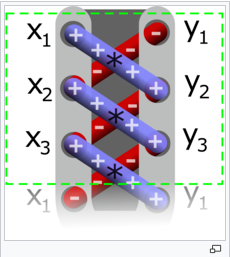
2.【鞋带公式】计算面积举例说明:
3. 方法一.【丢失精度】计算铜面积
将铜皮节点含有弧节点，全部转为折线节点, 转换后的弧长长度控制在0.1mm左右，当然弧长的长度值越小精度就越高，这样一来程序计算量就上去了，经测试弧长控制0.1mm比较合适。铜面积计算 精度不会丢失太多。
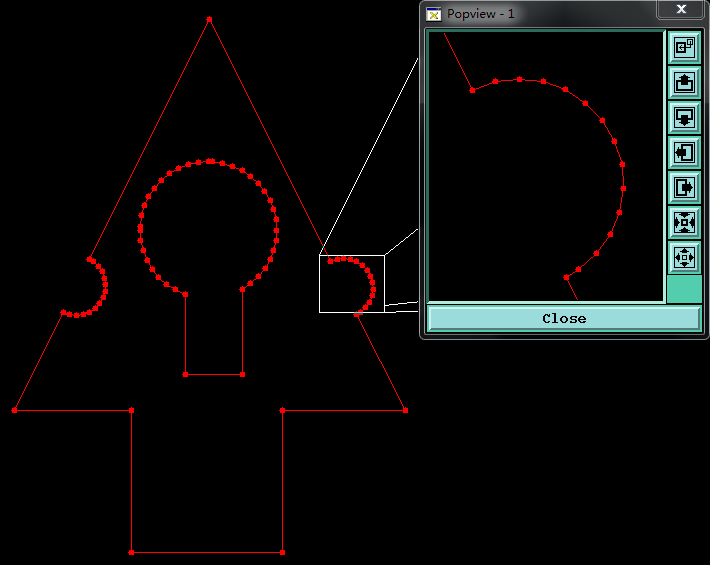
4.方法二.【精度】计算铜面积
将原有铜皮铜边形分为2部份
1.分解第1部份 折线多边形鞋带公式求解
2.分解第2部份 圆弧多边形扇形面积求解 (如何判断,圆弧多边形是删除，还是增加呢，下面有说明)
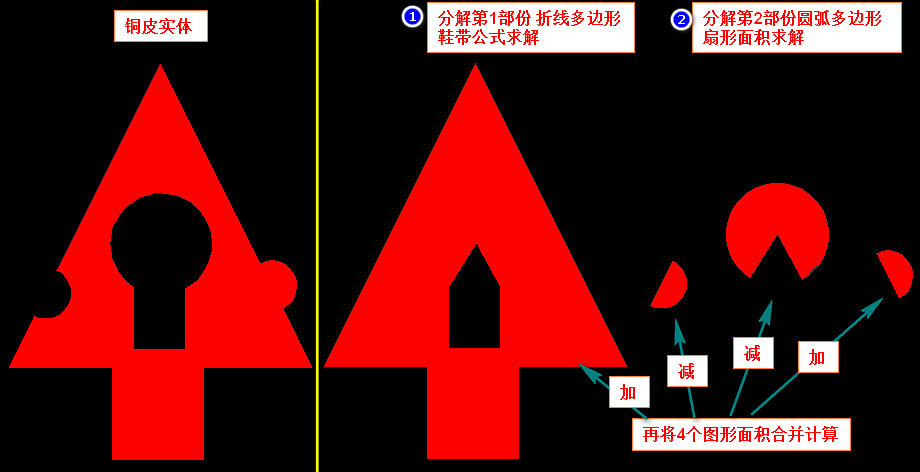
上面带来一个新的问题？ 图形面积合并计算,如何判断，哪些弧形多边形是【加】还是【减】呢
按下表的关系进行加减计算合并铜皮面积
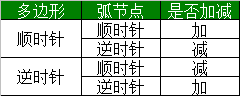
1.计算铜面积调用代码
//获取gtl 线路层(计算前转为Surface铜皮属性)
gLayer workLayerInfo = g.getFEATURES("gtl");
//1.【丢失精度】计算铜面积
var areaLayer = calc2.s_area(workLayerInfo.Slist);
//2. 【精度】计算铜面积
var areaLayer2 = calc2.s_area2(workLayerInfo.Slist);
//计算铜的多边形周长
var copperLenght = calc2.s_Length(workLayerInfo.Slist);
2.计算铜面积函数
/// <summary>
/// 【丢失精度】计算铜面积
/// </summary>
/// <param name="gS_list"></param>
/// <returns></returns>
public double s_area(List<gS> gS_list)
{
double SurfaceArea = ;
foreach (var gS_item in gS_list)
{
foreach (var Polyline in gS_item.sur_group)
{
var sur_list = s_2gSur_Point(Polyline.sur_list);
if (Polyline.is_hole)
SurfaceArea -= s_area(sur_list);
else
SurfaceArea += s_area(sur_list);
}
}
return SurfaceArea;
}
/// <summary>
/// 【丢失精度】计算铜面积
/// </summary>
/// <param name="gSur_Point_list"></param>
/// <returns></returns>
public double s_area(List<gSur_Point> gSur_Point_list)
{
int Point_Count = gSur_Point_list.Count() - ;
if (Point_Count < ) return ;
double PolylineArea = ;
double ArcArea = ;
for (int i = ; i <= Point_Count; i++)
{
PolylineArea += gSur_Point_list[i - ].p.x * gSur_Point_list[i].p.y - gSur_Point_list[i - ].p.y * gSur_Point_list[i].p.x;
}
PolylineArea = Math.Abs(PolylineArea * 0.5);
return PolylineArea;
}
/// <summary>
/// 【精度】计算铜面积
/// </summary>
/// <param name="gSur_Point_list"></param>
/// <returns></returns>
public double s_area2(List<gSur_Point> gSur_Point_list)
{
int Point_Count = gSur_Point_list.Count() - ;
if (Point_Count < ) return ;
double PolylineArea = ;
double ArcArea = ;
bool isCCW = s_isCCW(gSur_Point_list);
for (int i = ; i <= Point_Count; i++)
{
if (gSur_Point_list[i].type_point > )
{
double a_area = a_Area(gSur_Point_list[i - ].p, gSur_Point_list[i].p, gSur_Point_list[i + ].p, gSur_Point_list[i].type_point == );
if (isCCW)
{
if (gSur_Point_list[i].type_point == )
ArcArea += a_area;
else
ArcArea -= a_area;
}
else
{
if (gSur_Point_list[i].type_point == )
ArcArea -= a_area;
else
ArcArea += a_area;
}
}
PolylineArea += gSur_Point_list[i - ].p.x * gSur_Point_list[i].p.y - gSur_Point_list[i - ].p.y * gSur_Point_list[i].p.x;
}
PolylineArea = Math.Abs(PolylineArea * 0.5);
PolylineArea += ArcArea;
//var isCW = s_isCW(gSur_Point_list);
//PolylineArea += (isCCW ? -ArcArea : ArcArea);
return PolylineArea;
}
/// <summary>
/// 求弧Arc 扇形面积
/// </summary>
/// <param name="a"></param>
/// <returns></returns>
public double a_Area(gPoint ps, gPoint pc, gPoint pe, bool ccw, bool islg180deg = false)
{
double r_ = p2p_di(pc, ps);
return pi * r_ * r_ * a_Angle(ps, pc, pe, ccw, islg180deg) / ;
}
/// <summary>
/// 求弧Arc圆心角 3点 //后续改进 用叉积 与3P求角度求解 验证哪个效率高
/// </summary>
/// <param name="ps"></param>
/// <param name="pc"></param>
/// <param name="pe"></param>
/// <param name="ccw"></param>
/// <returns></returns>
public double a_Angle(gPoint ps, gPoint pc, gPoint pe, bool ccw, bool islg180deg = false)
{
double angle_s, angle_e, angle_sum;
if (ccw)
{
angle_s = p_ang(pc, pe);
angle_e = p_ang(pc, ps);
}
else
{
angle_s = p_ang(pc, ps);
angle_e = p_ang(pc, pe);
}
if (angle_s == ) { angle_s = ; }
if (angle_e >= angle_s)
{
angle_sum = - (angle_e - angle_s); //360 - Math.Abs(angle_s - angle_e);
}
else
{
angle_sum = angle_s - angle_e;//Math.Abs(angle_s - angle_e);
}
if (islg180deg && angle_sum > )
{
angle_sum = - angle_sum;
}
return angle_sum;
}
/// <summary>
/// 检测 Surface是否逆时针
/// </summary>
/// <param name="gSur_Point_list"></param>
/// <returns></returns>
public bool s_isCCW(List<gSur_Point> gSur_Point_list)
{
double d = ;
int n = gSur_Point_list.Count() - ;
for (int i = ; i < n; i++)
{
if (gSur_Point_list[i].type_point > ) continue;
int NextI = i + + (gSur_Point_list[i+ ].type_point > ? : );
d += -0.5 * (gSur_Point_list[NextI].p.y + gSur_Point_list[i].p.y) * (gSur_Point_list[NextI].p.x - gSur_Point_list[i].p.x);
}
return d > ;
}
/// <summary>
/// 将gSur_Point中含弧的节点转为线
/// </summary>
/// <param name="gSur_Point_list"></param>
/// <param name="val_">此数值表示:分段数值</param>
/// <param name="type_">代表值数值类型 【0】弧长 【1】角度 【2】弦长 </param>
/// <returns></returns>
public List<gSur_Point> s_2gSur_Point(List<gSur_Point> gSur_Point_list, double val_ = 1d, int type_ = )
{
List<gSur_Point> resultList = new List<gSur_Point>();
if (gSur_Point_list.Count > )
{
bool is_flag = false;
resultList.Add(gSur_Point_list[]);
for (int j = ; j < gSur_Point_list.Count; j++)
{
if (is_flag)
{
is_flag = false;
continue;
}
if (gSur_Point_list[j].type_point > )
{
var aData = new gA(gSur_Point_list[j - ].p, gSur_Point_list[j].p, gSur_Point_list[j + ].p, , gSur_Point_list[j].type_point == ? true : false);
var PlistData = a_2Plist(aData, val_, type_, true);
resultList.AddRange(PlistData.Select(tt => new gSur_Point(tt.p, )).ToList());
is_flag = true;
}
else
{
resultList.Add(gSur_Point_list[j]);
}
}
}
return resultList;
}
/// <summary>
/// 弧Arc 转点P组集
/// </summary>
/// <param name="a"></param>
/// <param name="val_">此数值表示:分段数值</param>
/// <param name="type_">代表值数值类型 【0】弧长 【1】角度 【2】弦长 </param>
/// <param name="is_avg">是否平均分布 </param>
/// <returns></returns>
public List<gPP> a_2Plist(gA a, double val_ = 0.1d, int type_ = , bool is_avg = false)
{
List<gPP> list_point = new List<gPP>();
gPP tempP;
tempP.p = a.ps;
tempP.symbols = a.symbols;
tempP.width = a.width;
list_point.Add(tempP); double avg_count;
double angle_val = ;
double rad_ = p2p_di(a.pc, a.pe);
double sum_alge = a_Angle(a);
if (type_ == ) // 【1】角度
{
angle_val = val_;
avg_count = (int)(Math.Floor(sum_alge / angle_val)); // 总角度/单角度
}
else if (type_ == ) //【2】弦长
{
angle_val = Math.Asin(val_ / (rad_ * )) * / pi;
avg_count = (int)(Math.Ceiling(sum_alge / angle_val) + eps) - ; // 总角度/单弦长
}
else // 【0】弧长
{
angle_val = val_ * / (pi * rad_);
avg_count = (int)(Math.Ceiling(sum_alge / angle_val) + eps) - ; // 总角度/单角度
//avg_count = (int)(Math.Ceiling(a_Lenght(a) / val_)) - 1; // 或 总弧长/单弧长
}
if (is_avg)
angle_val = sum_alge / avg_count;
if (avg_count > )
{
gPP centerP = tempP;
centerP.p = a.pc;
double angle_s = p_ang(a.pc, a.ps);
if (a.ccw) { angle_val = - angle_val; }
for (int i = ; i < avg_count; i++)
{
tempP = p_val_ang(centerP, rad_, angle_s - angle_val * i);
list_point.Add(tempP);
}
}
// if (!(zero(a.ps.x - a.pe.x) && zero(a.ps.y - a.pe.y)))
// {
// tempP.p = a.pe;
// list_point.Add(tempP);
// }
tempP.p = a.pe;
list_point.Add(tempP);
return list_point;
}
/// <summary>
/// 返回两点之间欧氏距离
/// </summary>
/// <param name="p1"></param>
/// <param name="p2"></param>
/// <returns></returns>
public double p2p_di(gPoint p1, gPoint p2)
{
return Math.Sqrt((p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y));
}
/// <summary>
/// 求弧Arc圆心角 //后续改进 用叉积 与3P求角度求解 验证哪个效率高
/// </summary>
/// <param name="a"></param>
/// <returns></returns>
public double a_Angle(gA a)
{
double angle_s, angle_e, angle_sum;
if (a.ccw)
{
angle_s = p_ang(a.pc, a.pe);
angle_e = p_ang(a.pc, a.ps);
}
else
{
angle_s = p_ang(a.pc, a.ps);
angle_e = p_ang(a.pc, a.pe);
}
if (angle_s == ) { angle_s = ; }
if (angle_e >= angle_s)
angle_sum = - Math.Abs(angle_s - angle_e);
else
angle_sum = Math.Abs(angle_s - angle_e);
return angle_sum;
}
/// <summary>
/// 求方位角
/// </summary>
/// <param name="ps"></param>
/// <param name="pe"></param>
/// <returns></returns>
public double p_ang(gPoint ps, gPoint pe)
{
double a_ang = Math.Atan((pe.y - ps.y) / (pe.x - ps.x)) / Math.PI * ;
//象限角 转方位角 计算所属象限 并求得方位角
if (pe.x >= ps.x && pe.y >= ps.y) //↗ 第一象限
{
return a_ang;
}
else if (!(pe.x >= ps.x) && pe.y >= ps.y) // ↖ 第二象限
{
return a_ang + ;
}
else if (!(pe.x >= ps.x) && !(pe.y >= ps.y)) //↙ 第三象限
{
return a_ang + ;
}
else if (pe.x >= ps.x && !(pe.y >= ps.y)) // ↘ 第四象限
{
return a_ang + ;
}
else
{
return a_ang;
}
}
/// <summary>
/// 求增量坐标
/// </summary>
/// <param name="ps">起点</param>
/// <param name="val">增量值</param>
/// <param name="ang_direction">角度</param>
/// <returns></returns>
public gPP p_val_ang(gPP ps, double val, double ang_direction)
{
gPP pe = ps;
pe.p.x = ps.p.x + val * Math.Cos(ang_direction * Math.PI / );
pe.p.y = ps.p.y + val * Math.Sin(ang_direction * Math.PI / );
return pe;
}
3.计算铜的多边形周长函数
/// <summary>
/// 求Surface 总周长
/// </summary>
/// <param name="gS_list"></param>
/// <returns></returns>
public double s_Length(List<gS> gS_list)
{
int Surface_Count = gS_list.Count();
double SurfaceArea = ;
foreach (var gS_item in gS_list)
{
foreach (var Polyline in gS_item.sur_group)
{
SurfaceArea += s_Length(Polyline.sur_list);
}
}
return SurfaceArea;
}
/// <summary>
/// 求Surface 总周长
/// </summary>
/// <param name="gSur_Point_list"></param>
/// <returns></returns>
public double s_Length(List<gSur_Point> gSur_Point_list)
{
double sum_lenght = ;
bool is_flag = false;
bool ccw = false;
for (int i = ; i < gSur_Point_list.Count; i++)
{
if (is_flag)
{
is_flag = false;
continue;
}
if (gSur_Point_list[i].type_point > )
{
if (gSur_Point_list[i].type_point == )
ccw = true;
else
ccw = false;
sum_lenght += a_Length(gSur_Point_list[i - ].p, gSur_Point_list[i].p, gSur_Point_list[i + ].p, ccw);
is_flag = true;
}
else
{
sum_lenght += l_Length(gSur_Point_list[i - ].p, gSur_Point_list[i].p);
}
}
return sum_lenght;
}
/// <summary>
/// 求弧Arc长度 3点
/// </summary>
/// <param name="ps"></param>
/// <param name="pc"></param>
/// <param name="pe"></param>
/// <returns></returns>
public double a_Length(gPoint ps, gPoint pc, gPoint pe, bool ccw = false)
{
return pi / * p2p_di(pc, ps) * a_Angle(ps, pc, pe, ccw);
}
/// <summary>
/// 求线Line长度 2点
/// </summary>
/// <param name="ps"></param>
/// <param name="pe"></param>
/// <returns></returns>
public double l_Length(gPoint ps, gPoint pe)
{
return Math.Sqrt((ps.x - pe.x) * (ps.x - pe.x) + (ps.y - pe.y) * (ps.y - pe.y));
}
4.数据结构
/// <summary>
/// Surface 坐标泛型集类1
/// </summary>
public class gSur_Point
{
public gSur_Point()
{ }
public gSur_Point(double x_val, double y_val, byte type_point_)
{
this.p.x = x_val;
this.p.y = y_val;
this.type_point = type_point_;
}
public gSur_Point(gPoint p, byte type_point_)
{
this.p = p;
this.type_point = type_point_;
}
public gPoint p;
/// <summary>
/// 0为折点 1为顺时针 2为逆时针
/// </summary>
public byte type_point { get; set; } = ;
/// <summary>
/// 值
/// </summary>
public double Value { get; set; } = ;
}
/// <summary>
/// Surface 坐标泛型集类2
/// </summary>
public class gSur_list
{
public List<gSur_Point> sur_list = new List<gSur_Point>();
/// <summary>
/// 是否为空洞
/// </summary>
public bool is_hole { get; set; }
/// <summary>
/// 是否逆时针
/// </summary>
public bool is_ccw { get; set; }
}
/// <summary>
/// Surface 坐标泛型集类3
/// </summary>
public class gS
{
public List<gSur_list> sur_group = new List<gSur_list>();
/// <summary>
/// 是否为负 polarity-- P N
/// </summary>
public bool negative { get; set; }
public string attribut { get; set; }
}
/// <summary>
/// 点 数据类型 (XY)
/// </summary>
public struct gPoint
{
public gPoint(gPoint p_)
{
this.x = p_.x;
this.y = p_.y;
}
public gPoint(double x_val, double y_val)
{
this.x = x_val;
this.y = y_val;
}
public double x;
public double y;
public static gPoint operator +(gPoint p1, gPoint p2)
{
p1.x += p2.x;
p1.y += p2.y;
return p1;
}
public static gPoint operator -(gPoint p1, gPoint p2)
{
p1.x -= p2.x;
p1.y -= p2.y;
return p1;
}
}
/// <summary>
/// ARC 数据类型
/// </summary>
public struct gA
{
public gA(double ps_x, double ps_y, double pc_x, double pc_y, double pe_x, double pe_y, double width_, bool ccw_)
{
this.ps = new gPoint(ps_x, ps_y);
this.pc = new gPoint(pc_x, pc_y);
this.pe = new gPoint(pe_x, pe_y);
this.negative = false;
this.ccw = ccw_;
this.symbols = "r" + width_.ToString();
this.attribut = string.Empty;
this.width = width_;
}
public gA(gPoint ps_, gPoint pc_, gPoint pe_, double width_, bool ccw_ = false)
{
this.ps = ps_;
this.pc = pc_;
this.pe = pe_;
this.negative = false;
this.ccw = ccw_;
this.symbols = "r" + width_.ToString();
this.attribut = string.Empty;
this.width = width_;
}
public gPoint ps;
public gPoint pe;
public gPoint pc;
public bool negative;//polarity-- positive negative
public bool ccw; //direction-- cw ccw
public string symbols;
public string attribut;
public double width;
public static gA operator +(gA arc1, gPoint move_p)
{
arc1.ps += move_p;
arc1.pe += move_p;
arc1.pc += move_p;
return arc1;
}
public static gA operator +(gA arc1, gPP move_p)
{
arc1.ps += move_p.p;
arc1.pe += move_p.p;
arc1.pc += move_p.p;
return arc1;
}
public static gA operator +(gA arc1, gP move_p)
{
arc1.ps += move_p.p;
arc1.pe += move_p.p;
arc1.pc += move_p.p;
return arc1;
}
public static gA operator -(gA arc1, gPoint move_p)
{
arc1.ps -= move_p;
arc1.pe -= move_p;
arc1.pc -= move_p;
return arc1;
}
public static gA operator -(gA arc1, gPP move_p)
{
arc1.ps -= move_p.p;
arc1.pe -= move_p.p;
arc1.pc -= move_p.p;
return arc1;
}
public static gA operator -(gA arc1, gP move_p)
{
arc1.ps -= move_p.p;
arc1.pe -= move_p.p;
arc1.pc -= move_p.p;
return arc1;
}
}
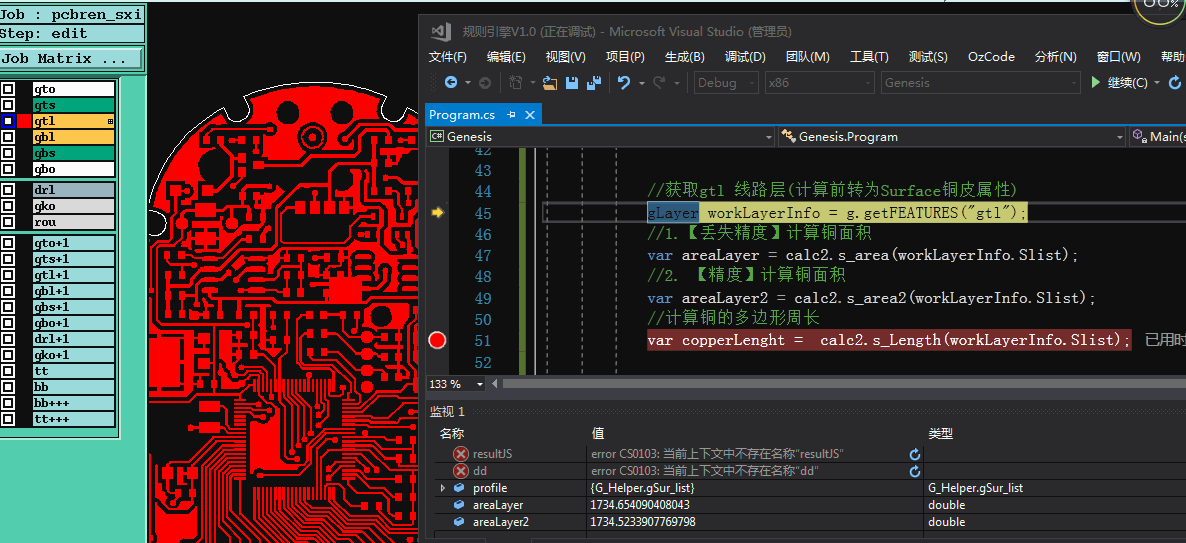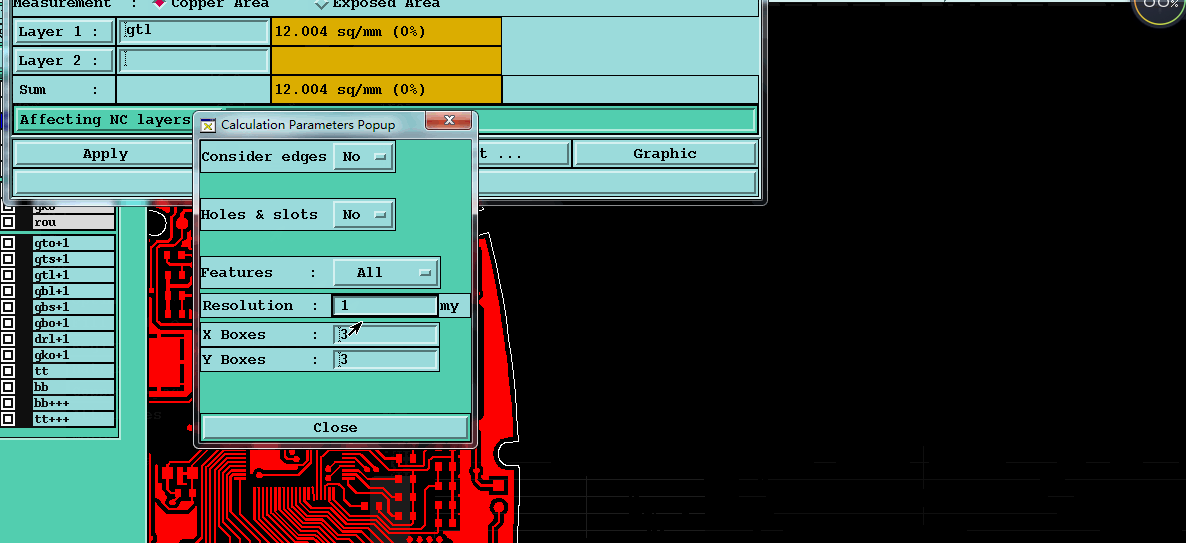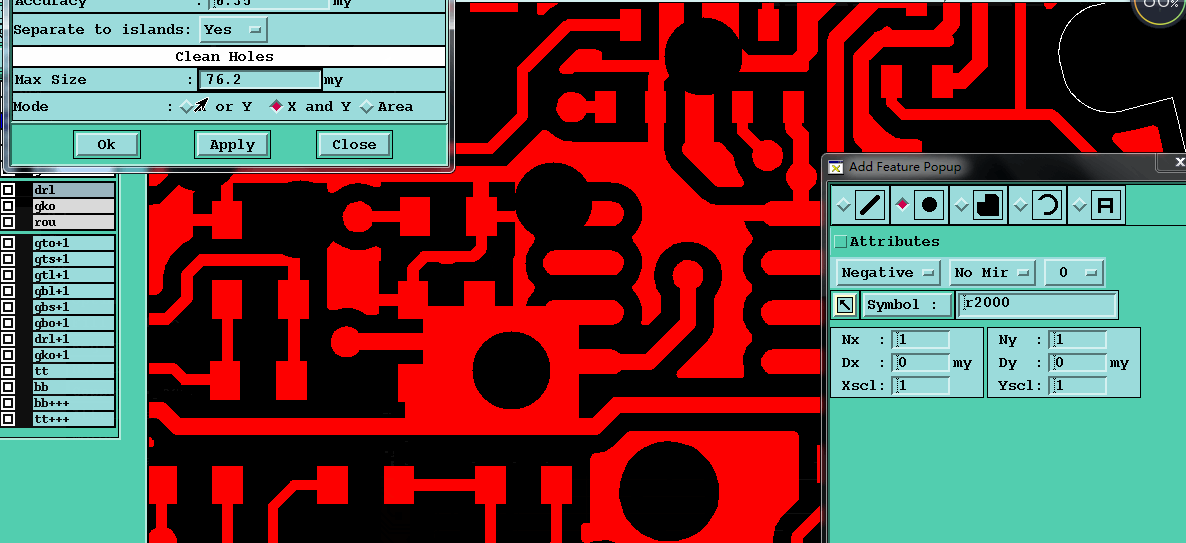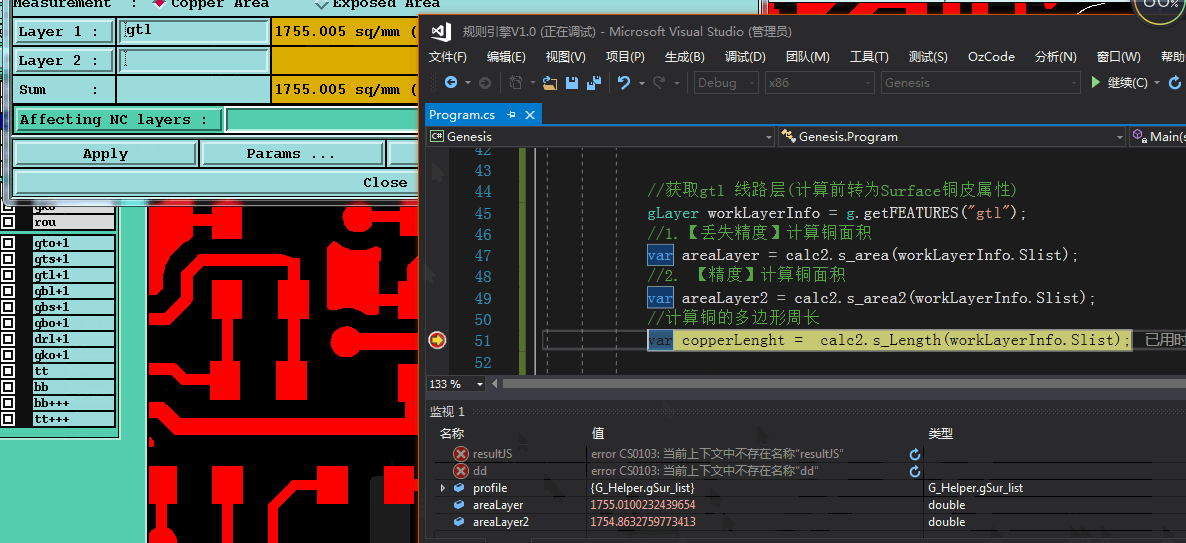
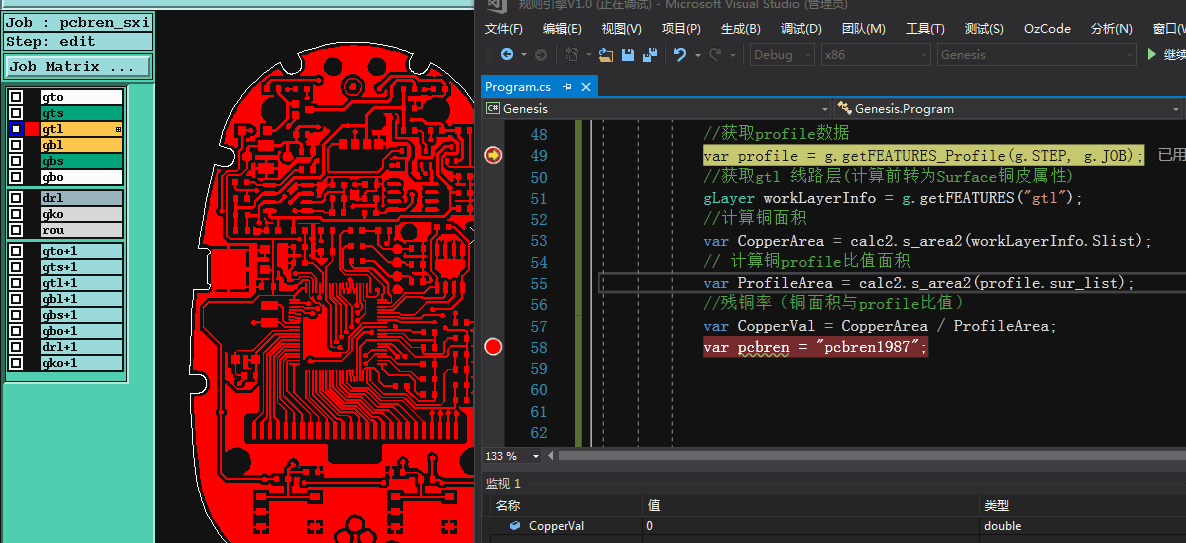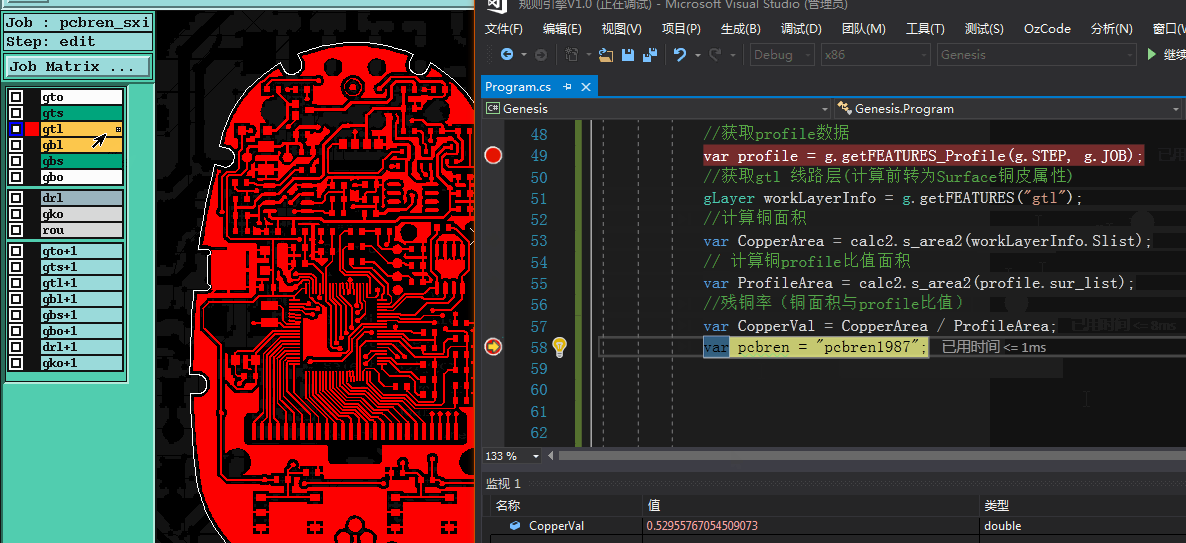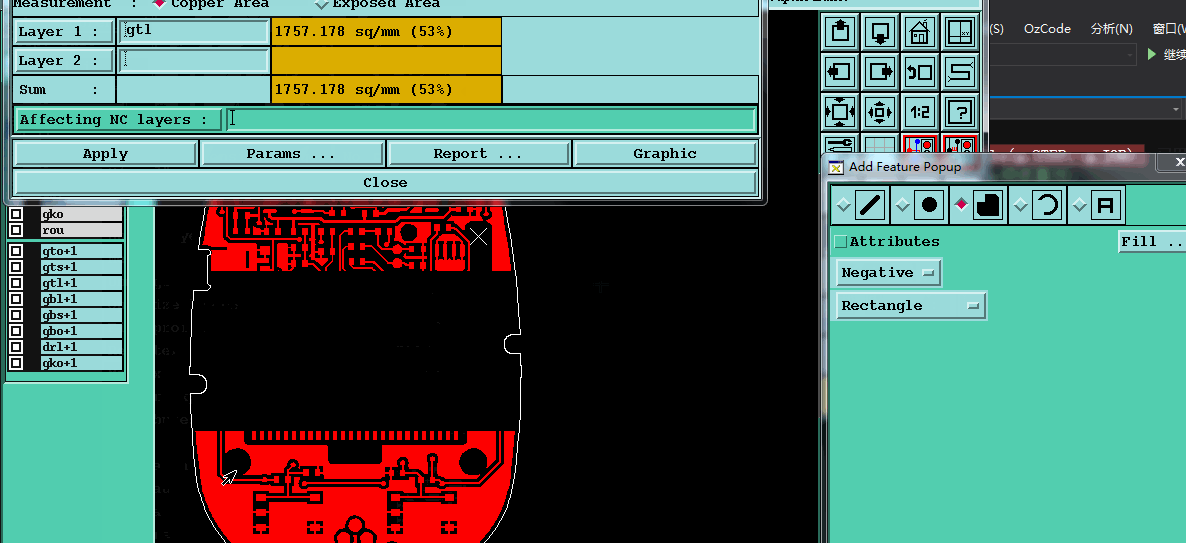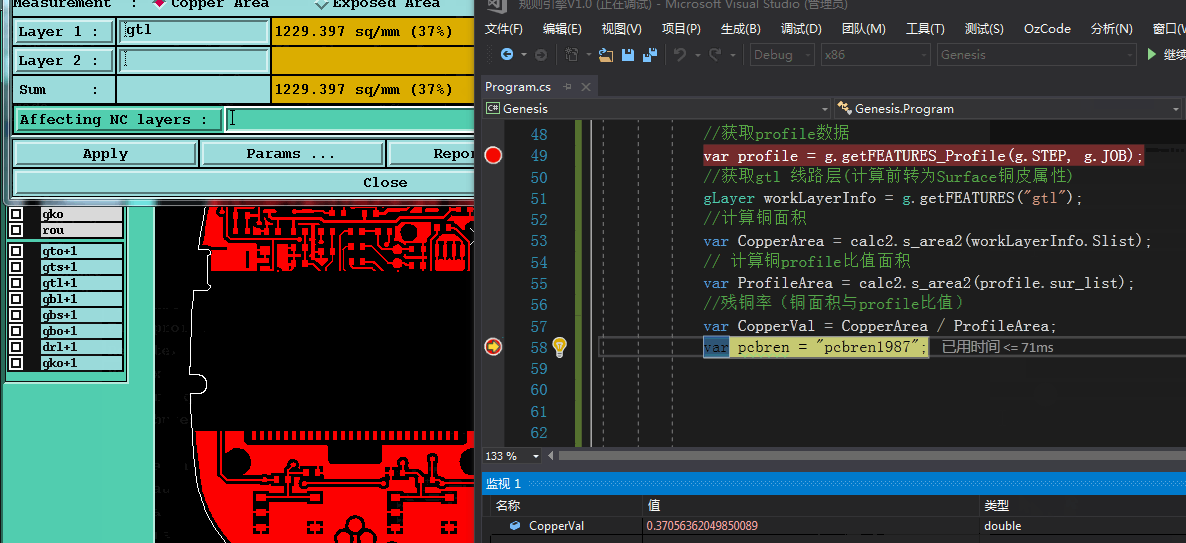
【残铜率】公式=【铜皮面积】除以 【Profile面积】
正常来说profile形状为矩形(开料决定的),计算矩形面积非常容易，但如果是profile尺寸为异形,求profile的面积和铜面积计算方法也是一样的， 异形的profile数据结构和铜【Surface】数据结构类似的。下图以异形profile为例，计算残铜率结果和genesis保持一致
经测试，发现程序计算出来铜面积与genesis铜面积计算存在少量的偏差(猜测奥宝为了达到越大规模铜面积计算或计算铜面积前在做数据转换与检测，而采用丢失精度计算铜面积达到快速计算铜面积的目的),用此方法计算铜面积,不管是计算速度上，还是铜面积精度上面都已超越genesis计算（仅仅个人测试对比结果）.
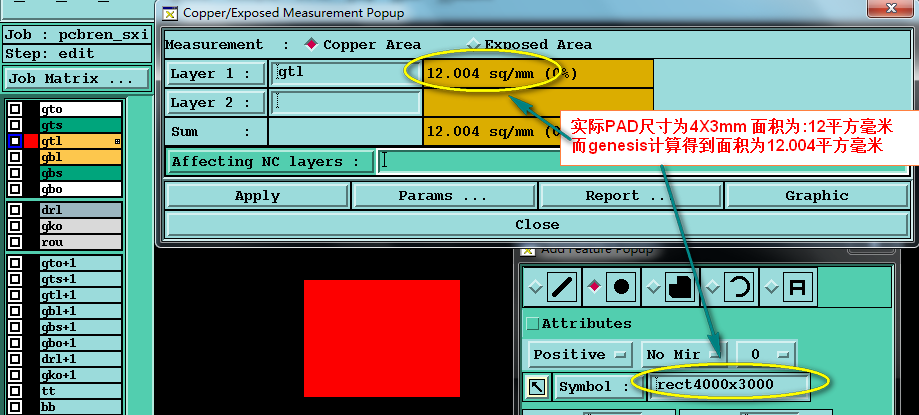
下例:genesis计算铜面积存一定偏差,实际PAD尺寸为4X3mm 面积为:12平方毫米 而genesis计算得到面积为12.004平方毫米
PCB 线路铜皮面积(残铜率)计算的实现方法的更多相关文章
- 通过经纬度坐标计算距离的方法（经纬度距离计算）ZZ
通过经纬度坐标计算距离的方法(经纬度距离计算) 最近在网上搜索“通过经纬度坐标计算距离的方法”,发现网上大部分都是如下的代码: #define PI 3.14159265 static double ...
- 你的GAN训练得如何--GAN 的召回率（多样性）和精确率（图像质量）方法评估
生成对抗网络(GAN)是当今最流行的图像生成方法之一,但评估和比较 GAN 产生的图像却极具挑战性.之前许多针对 GAN 合成图像的研究都只用了主观视觉评估,一些定量标准直到最近才开始出现.本文认为现 ...
- 关于字符串计算size的方法比较
往往字符串需要计算size来满足UI排版的自适应的需要,而一般字符串也是放在UILabel里的. 而在计算size的方法里,一般有两种方式(deprecated的就不说了). NSString的方法 ...
- vue的计算属性与方法的不同
计算属性 vue的模板里可以使用表达式,但是它的设计初衷是用于简单计算,在模板中放入太多逻辑会让模板过重且难以维护.例如: <div id="example"> {{ ...
- 编写一个ComputerAverage抽象类，类中有一个抽象方法求平均分average，可以有参数。定义 Gymnastics 类和 School 类，它们都是 ComputerAverage 的子类。Gymnastics 类中计算选手的平均成绩的方法是去掉一个最低分，去掉一个最高分，然后求平均分；School 中计算平均分的方法是所有科目的分数之和除以总科目数。 要求：定义ComputerAv
题目: 编写一个ComputerAverage抽象类,类中有一个抽象方法求平均分average,可以有参数. 定义 Gymnastics 类和 School 类,它们都是 ComputerAverag ...
- python计算时间差的方法
本文实例讲述了python计算时间差的方法.分享给大家供大家参考.具体分析如下: 1.问题: 给定你两个日期,如何计算这两个日期之间间隔几天,几个星期,几个月,几年? 2.解决方法: 标准模块date ...
- MySQL的性能指标计算和优化方法
MySQL的性能指标计算和优化方法1 QPS计算(每秒查询数) 针对MyISAM引擎为主的DB mysql> show global status like 'questions';+----- ...
- PCB 加投率计算实现基本原理--K最近邻算法（KNN）
PCB行业中,客户订购5000pcs,在投料时不会直接投5000pcs,因为实际在生产过程不可避免的造成PCB报废, 所以在生产前需计划多投一定比例的板板, 例:订单 量是5000pcs,加投3%,那 ...
- lcd参数解释及刷新率计算，LCD时序
一.LCD显示图像的过程如下: 其中,VSYNC和HSYNC是有宽度的,加上后如下: 参数解释: HBP(Horizontal Back Porch)水平后沿:在每行或每列的象素数据开始输出时要插入的 ...
随机推荐
- Linux常用C函数-接口处理篇（网络通信函数)
接口处理篇accept,bind,connect,endprotoent,endservent,getsockopt,htonl,htons,inet_addr,inet_aton,inet_ntoa ...
- 空暇时候思考2（'\0'等价于数字0还是字符0）
/********************************************************************** * * Copyright (c)2015,WK Stu ...
- centos 重新获取IP hdcp 模式
centos 重新获取IP hdcp 模式 dhclient -r →release dhclient →renew
- grunt 试用笔记
Gruntjs是JavaScript项目的构建工具,也是基于node的一个命令行工具.很多开源JS项目都是使用它搭建.如jQuery.Qunit.CanJS等.它有以下作用 合并JS文件压缩JS文件单 ...
- Java学习之集合
1.ArrayList:采用数组的形式保存对象,这种方式将对象保存在连续的位置中,所以查询效率比较高,但是插入删除时麻烦,并且ArrayList不是线程安全的. 2.Vector:保存对象的方式与Ar ...
- SpringBoot学习之快速入门创建
maven构建项目 1.访问http://start.spring.io/,进入快速创建工程的主页 可参考下图所示: 2.选择构建工具Maven Project.Spring Boot版本1.3.6以 ...
- 【手记】走近科学之为什么JObject不能调用LINQ扩展方法
Json.NET的JObject明明实现了IEnumerable<T>,具体来说是IEnumerable<KeyValuePair<string, JToken>> ...
- plsql 无需配置客户端连接.
plsql 无需配置客户端连接. (DESCRIPTION=(ADDRESS_LIST=(ADDRESS=(PROTOCOL=TCP)(HOST=192.168.0.5)(PORT=1521)))(C ...
- HDU 1085 Holding Bin-Laden Captive!(母函数，或者找规律）
Holding Bin-Laden Captive! Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Ja ...
- 设计模式入门之訪问者模式Visitor
//訪问者模式定义:表示一个作用于某对象结构中的各个元素的操作,它使你能够在不改变各元素类的前提下定义作用于这些元素的新操作. //从定义上看.这个模式跟装饰模式的定义非常类似(动态地给一个对象加入一 ...