用贝叶斯定理解决三门问题并用Python进行模拟（Bayes' Rule Monty Hall Problem Simulation Python）

三门问题（Monty Hall problem）也称为蒙提霍尔问题或蒙提霍尔悖论，出自美国的电视游戏节目《Let’s Make a Deal》。问题名字来自该节目的主持人蒙提·霍尔（Monty Hall）。

这个游戏的玩法是：参赛者会看见三扇关闭的门，其中一扇门后面有一辆汽车，选中后面有车的那扇门就可以赢得该汽车，而另外两扇门后面则各藏有一只山羊。当参赛者选定了一扇门，但未去开启它的时候，节目主持人会开启剩下两扇门中的一扇，露出其中一只山羊。主持人其后会问参赛者要不要更换其初始的选择，选另一扇仍然关上的门。

那么问题来了，参赛者到底要不要更换其初始的选择呢？

解决这个问题需要用到贝叶斯定理：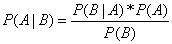

让我们选一个特定的例子来看看：假设三扇门分别为Door A，Door  B，Door C，并且参赛者初始选定了Door A，然后主持人展示了Door  B。那么参赛者是坚持选择Door A还是更换成Door C呢？这就要根据Door A和Door C哪个门后汽车出现的概率较大决定了。

也就是说，我们需要解决P(Door A=car|Door A is selected, Door  B is revealed)和P(Door C=car|Door A is selected, Door  B is revealed)哪个大的问题。

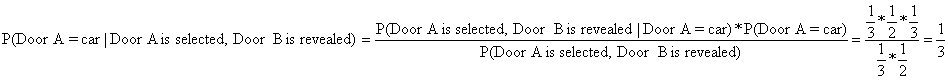
首先，每个门后有车的概率都是1/3：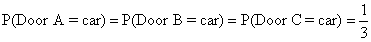

其次，如果Door A门后有汽车，那么Door A被选择的几率是1/3，假设初始选择了Door A，那么Door B被主持人打开的几率是1/2：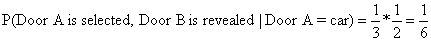

再次，普通情况下，Door A被选择的几率是1/3，Door B被主持人打开的几率是1/2（因为已经有一扇门被选择了，选择的门不能被打开）：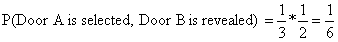

同理，如果Door C门后有汽车，那么Door A被选择的几率是1/3，假设初始选择了Door A，那么Door B被主持人打开的几率是1：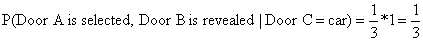

因此，我们可以看到，P(Door C=car|Door A is selected, Door  B is revealed)是P(Door A=car|Door A is selected, Door  B is revealed)的两倍。也就是说，更换初始的选择将会使我们的获胜几率提高2倍！

可以用probability tree来帮助理解一下：

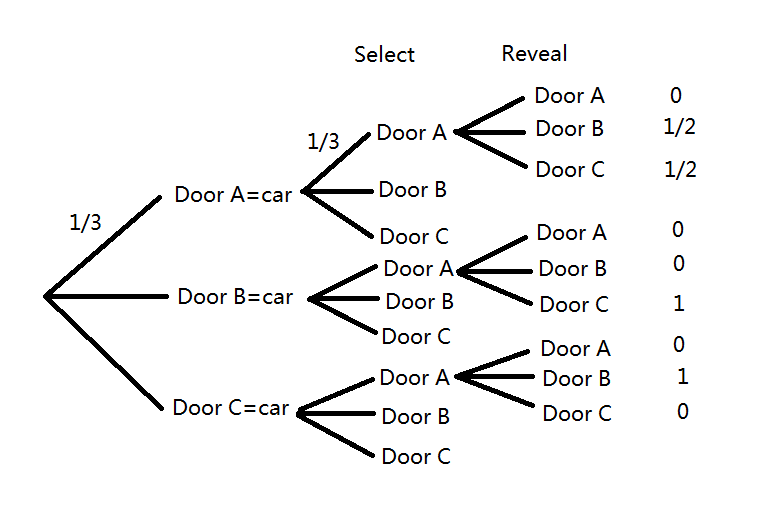
如果对上面的计算公式还有疑问，那么让我们用计算机来模拟一下：

from random import randint
from random import choice

N = 1000

def simulate(N):
    m=0   #设置不更换初始选择赢得汽车的次数
    n=0   #设置更换初始选择赢得汽车的次数
    for i in range(N):  #模拟1000次游戏
        win=randint(1,3)  #设置藏有汽车的门，在1-3之间随机选出
        bet1=randint(1,3)   #设置初始选择的门，在1-3之间随机选出
        remain=[i for i in range(1,4) if i!=win and i!=bet1]  #剩余可选的门（除去初始选择的门和藏有汽车的门）
        monty_reveal=choice(remain)  #monty会在剩余可选的门中选择一扇门打开
        bet2=6-bet1-monty_reveal  #bet2表示更换初始选择（用6减是因为三扇门加起来等于6）
        if bet1==win:  #如果初始选择和藏有汽车的门吻合，那么初始选择的获胜次数+1
            m+=1
        if bet2==win:  ##如果更换初始选择的bet2和藏有汽车的门吻合，那么bet2的获胜次数+1
            n+=1
    return n/m

print(simulate(N))

2.0211480362537766

最后的结果： 更换初始选择获胜的次数差不多是不更换初始选择获胜次数的两倍。

三门问题是有些反直觉的，我们可以这样来理解：当参赛者选择Door A时，他的获胜概率是1/3，当主持人展示了Door B门后没有汽车以后，这个信息并没有给参赛者的初始选择带来任何有用的信息 ，选择Door A获胜的概率仍然是1/3，但是鉴于选择Door B获胜的概率降为了0，因此选择Door C获胜的概率变为1-1/3，也就是2/3。

参考：https://classroom.udacity.com/courses/st101/lessons/48744119/concepts/484806120923