模拟赛 yjqb

对于这种“不能交叉”的条件，不是很好处理。那么就考虑一下dp

dp[i][j]表示，考虑A中用前i个，考虑连接B中用前j个，最大匹配。（类似LCS的DP）

转移：dp[i][j]=max(dp[i][j-1],dp[i-1][j])当li<=j<=ri时，dp[i][j]=max(dp[i][j],dp[i-1][j-1]+1)

这样可以保证一定不会交叉，而且不会共用匹配点

O(N^2）

看起来非常无法优化。而且我们还没有好好利用区间连边的特点。

观察转移的特点，

一个发现是，这是一个前缀取max，并且某些dp数值的位置+1

由于要和前面的i取max，

那么，把函数键值化，

对于考虑到第i个点，

图像是：

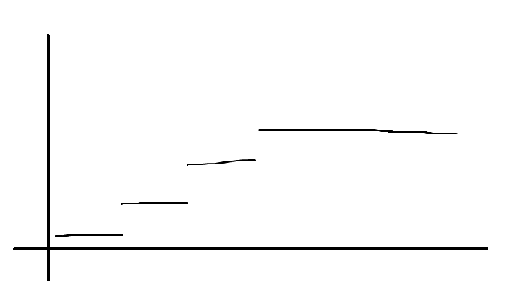
一个分段函数！

考虑如果新加入一个点i的话，在此基础上造成什么影响。

为了方便理解，考虑用滚动数组

dp[j]=max(dp[j],dp[j-1]+1)

这个dp[j]可以直接理解为上一次留下的dp值。（当然转移是倒序循环）

dp[j]=max(dp[j-1],dp[j])这个要正序循环

发现，对于分段函数造成的影响，是一段区间！

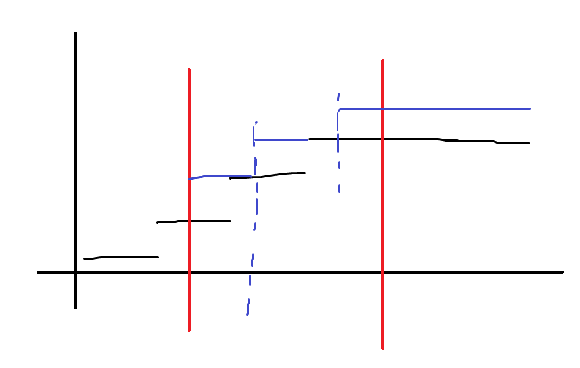
由于dp[j]=max(dp[j],dp[j-1]+1)，注意每个分段函数的左端点是不会变化的。

并且，+1的转移都是dp[j]=max(dp[j],dp[j-1]+1)

所以，分段函数的落差都恰好是1！！！

如果可以维护好分段函数，那么最后最高的函数就是ans

怎么维护？

发现这个函数的变化，本质上是把更新区间中涉及到的分段函数向右移动一步，再向上移动一步得到的新的图像！

于是可以打标记了！

这个函数的区间提取，如果用线段树做的话，提取会非常麻烦。而且左移上移怎么处理？！？！

这么灵活的移动，只能交给平衡树了！

ywy_c_asm的大力讨论法：

用三元组[l,r,val]表示每个分段函数的左右端点和高度（函数值）

很多麻烦的事情：

1.边界涉及到函数分离，函数合并。

2.边界可能是某些函数的左端点，

3.和后面的合并？没有后继怎么办？

4.[L,R]只有一个分段函数？要特判

5.[L,R]有两个分段函数?由于不能直接把后面的函数合并到前驱再--r那么简单（其实好像可以？）反正特判比较保险

6.[L,R]有多个分段函数？这时候就要区间打标记了。

7.merge函数那个并入哪一个？

8.split函数，从哪里断开？剩下的l，r是什么？

还有一些splay的基本操作（我写的splay）

1.pre，bac前驱后继，记得pushdown

2.kth，记得pushdown

3.tag的标记打好。

4.左右位置放上空节点方便提取区间。

。。。。。。。。。

还有一堆细节

。。。。。。。。。

放上代码：

大概4+4+4=12种讨论？

删掉注释250行左右

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define ls t[x].ch[0]
#define rs t[x].ch[1]
#define numb (ch^'0')
using namespace std;
typedef long long ll;
il void rd(int &x){
    char ch;x=;bool fl=false;
    while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*+numb);
    (fl==true)&&(x=-x);
}
namespace Miracle{
const int N=+;
const int nd=;
const int st=;
int n;
struct node{
    int l,r,v;
    int fa,ch[];
    int tag;
    node(){}
    node(int ll,int rr,int vv){
        l=ll,r=rr,v=vv;
        ch[]=ch[]=;
        fa=;
        tag=;
    }
    void op(){
        cout<<" left "<<l<<" right "<<r<<" val "<<v<<endl;
        cout<<" father "<<fa<<" son1 "<<ch[]<<" son2 "<<ch[]<<" tag "<<tag<<endl;
    }
}t[N];
int cnt;
int rt;
void tag(int x,int c){
    t[x].tag+=c;
    t[x].v+=c;
    t[x].l+=c;
    t[x].r+=c;
}
void pushdown(int x){
    if(!t[x].tag) return;
//    cout<<" pushdown "<<x<<" "<<t[x].tag<<endl;
    tag(ls,t[x].tag);
    tag(rs,t[x].tag);
    t[x].tag=;
}
void rotate(int x){
    int y=t[x].fa,d=t[y].ch[]==x;
    t[t[y].ch[d]=t[x].ch[!d]].fa=y;
    t[t[x].fa=t[y].fa].ch[t[t[y].fa].ch[]==y]=x;
    t[t[x].ch[!d]=y].fa=x;
}
void splay(int x,int f){
    while(t[x].fa!=f){
        int y=t[x].fa,z=t[y].fa;
        if(z!=f){
            rotate((t[z].ch[]==y)&&(t[y].ch[]==x)?y:x);
        }
        rotate(x);
    }
    if(f==) rt=x;
}
int pre(int x){
    splay(x,);
    x=t[x].ch[];
    if(!x) return -;
    pushdown(x);
    while(t[x].ch[]) {
        x=t[x].ch[];
        pushdown(x);
    }
    return x;
}
int bac(int x){
//    cout<<" fin bac "<<x<<" "<<t[x].ch[0]<<endl;
    splay(x,);
    x=t[x].ch[];
//    cout<<" ch[1] "<<x<<" "<<t[x].ch[0]<<endl;
    if(!x) return -;
    pushdown(x);
    while(t[x].ch[]) {
        x=t[x].ch[];
        pushdown(x);
    }
    return x;
}
int kth(int k){
//    cout<<" find kth "<<k<<endl;
    int x=rt;
    while(x){
        pushdown(x);
    //    cout<<" xx "<<x<<endl;t[x].op();
        if(t[x].l<=k&&k<=t[x].r) return x;
        else if(t[x].l>k) x=t[x].ch[];
        else if(t[x].r<k) x=t[x].ch[];
    }
    return -;//warning !!!
}
void merge(int x,int y){
    //cout<<" merge "<<x<<" "<<y<<endl;
    splay(x,);splay(y,x);
    t[t[x].ch[]=t[y].ch[]].fa=x;
    t[x].r=t[y].r;
}
void split(int x,int l,int r){
    ++cnt;
    t[cnt]=node(l,r,t[x].v);
    t[t[cnt].ch[]=t[x].ch[]].fa=cnt;
    t[cnt].fa=x;
    t[x].ch[]=cnt;
    t[x].r=l-;//warning!!
}
void wrk(int L,int R){
//    cout<<" wrking ---------------------"<<L<<" "<<R<<endl;
    int lc=kth(L),rc=kth(R);
    //cout<<" lc "<<lc<<endl;t[lc].op();
    //cout<<" rc "<<rc<<endl;t[rc].op();
    if(lc==rc){
    //    cout<<" Sol 1*****"<<endl;
        if(L==R){
        //    cout<<" 1.1%%"<<endl;
            if(t[lc].l==L){
//                int pr=pre(lc);
//                if(pr==st){
//                    int bc=bac(lc);
//                    if(bc==nd){
//                        ++t[lc].v;
//                    }else{
//                        merge(lc,bc);
//
//                    }
//                }
                return;
            }
            else if(t[lc].r==L){
                int bc=bac(lc);
                if(bc==nd){//las cur
                    split(lc,L,R);
                    ++t[cnt].v;
                }else{
                    t[bc].l=L;
                    t[lc].r=L-;
                }
                return;
            }else{
                //cout<<" 1.1.3$$$ "<<endl;
                int bc=bac(lc);
            //    cout<<" bc "<<bc<<endl;
                if(bc==nd){
                    split(lc,L,t[lc].r);
                    ++t[cnt].v;
                }else{
                    t[bc].l=L;
                    t[lc].r=L-;
                }
                return;
            }
        }else{
            if(t[lc].l==L){
                int bc=bac(lc);
                if(bc==nd){//las cur
                    split(lc,t[lc].l+,t[lc].r);
                    ++t[cnt].v;
                }else{
                    t[bc].l=t[lc].l+;
                    t[lc].r=t[lc].l;
                }
                return;
            }else{
                int bc=bac(lc);
                if(bc==nd){//las cur
                    split(lc,L,t[lc].r);
                    ++t[cnt].v;
                }else{
                    t[bc].l=L;
                    t[lc].r=L-;
                }
                return;
            }
        }
        return;
    }
    int pr=pre(rc);
    if(pr==lc){
        if(t[lc].l==L&&t[rc].l==R){
            t[lc].r=L;
            t[rc].l=L+;
        }else if(t[lc].l==L){
            int bc=bac(rc);
            if(bc==nd){
                split(rc,t[rc].l+,t[rc].r);
                ++t[cnt].v;
            }else{
                t[bc].l=t[rc].l+;
                t[rc].r=t[rc].l;
            }
            t[rc].l=L+;
            t[lc].r=L;
        }else if(t[rc].l==R){
            t[rc].l=L;
            t[lc].r=L-;
        }else{
            int bc=bac(rc);
            if(bc==nd){
                split(rc,t[rc].l+,t[rc].r);
                ++t[cnt].v;
            }else{
                t[bc].l=t[rc].l+;
                t[rc].r=t[rc].l;
            }
            t[rc].l=L;
            t[lc].r=L-;
        }
    }
    else{
        //cout<<" Sol 3*******"<<endl;
        if(t[rc].l==R){
            merge(pr,rc);
            rc=pr;
            t[rc].r--;
        }else{
        //    cout<<" 3.1.2$$$"<<endl;
            int bc=bac(rc);
        //    cout<<" bac "<<bc<<endl;
            if(bc==nd){
                t[rc].r--;
            }else{
                merge(rc,bc);
                t[rc].r--;
            }
        }

        if(t[lc].l==L){
            split(lc,L,t[lc].r);
            t[lc].r=L;
            lc=cnt;
        }else{
            split(lc,L-,t[lc].r);
            t[lc].r=L-;
            lc=cnt;
        }

        int LL=pre(lc),RR=bac(rc);

        splay(LL,);splay(RR,LL);
        //cout<<" LL "<<LL<<endl;t[LL].op();

    //    cout<<" RR "<<RR<<endl;t[RR].op();
        tag(t[RR].ch[],);
    }
}
int calc(){
    splay(nd,);
    int cur=pre(nd);
    return t[cur].v;
}
int main(){
    rd(n);
    rt=;
    t[++cnt]=node(-,-,);
    t[cnt].fa=;
    t[cnt].ch[]=cnt+;++cnt;

    t[cnt]=node(,n,);
    t[cnt].fa=;
    t[cnt].ch[]=cnt+;++cnt;

    t[cnt]=node(n+,n+,);
    t[cnt].fa=;

//    cout<<t[1].fa<<" "<<t[1].ch[0]<<" "<<t[1].ch[1]<<endl;
//    cout<<t[2].fa<<" "<<t[2].ch[0]<<" "<<t[2].ch[1]<<endl;
//    cout<<t[3].fa<<" "<<t[3].ch[0]<<" "<<t[3].ch[1]<<endl;

    int L,R;
    for(reg i=;i<=n;++i){
        rd(L);rd(R);
        wrk(L,R);
    //    cout<<" after wrk "<<cnt<<endl;
    }
    printf("%d\n",calc());
    return ;
}

}
signed main(){
    Miracle::main();
    return ;
}

/*
   Author: *Miracle*
   Date: 2018/12/24 13:54:20
*/

太TMD麻烦了。。。。。（要不是为了锻炼码力才不写）

发现之前的方法麻烦的地方在于，维护[l,r]这个区间要来回讨论。函数值+1要讨论。左端点要讨论。split，merge要讨论。。。

落差都是1，怎么利用呢？

用一些点来维护分段函数！

每个点表示这个分段函数的左端点。维护点的横坐标

修改的时候，

[l,r)的左端点集体右移，加入一个l点，把>=r最小的点删除。没了。

原因是，我们不记录高度，一个函数值左边的点的个数，就是函数值的大小!

所以，插入一个点相当于对后面的所有点高度+1，只需要将点向右平移。

同时，代替合并函数值的是，把>=r的点删除掉。

一个关键点在r的位置，并不能+1，所以是开区间。

最后点的个数就是函数值！

总结：

1.DP首先要想到。观察转移，得到分段函数的性质

2.分段函数的移动，可以模式化，所以可以打标记。

3.平衡树维护分段函数，以及一些小技巧。