c/c++求解图的关键路径 critical path

c/c++求解图的关键路径 critical path

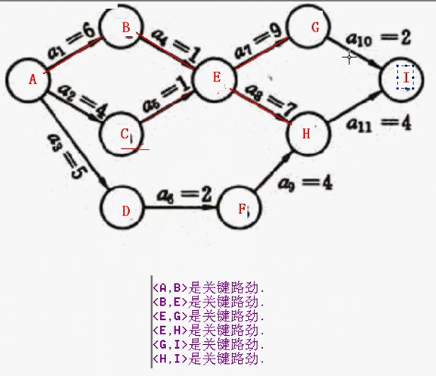
上图表示一个工程，工程以V1为起始子工程，V9为终止子工程。

由图可以看出，要开工V5工程，必须在完成工程V2和V3后才可以。

完成V2需要a1（6）个小时，完成V3需要a2(4)个小时。假设V2和V3同时开工，V3就会提前2个小时完工，但是这时V2还没有完工，所以V5还不能开始。所以为了要开工V5必须V2要完成，V3即使晚开工2个小时，也不会耽误V5的开工，所以V2就是V5的 关键路径（Critical Path）。

有2个问题：(1)完成整个工程至少需要多少时间。(2)哪些子工程是影响总工程进度的关键？

(1)的答案：关键路径上的时间总和是完成整个工程至少需要的时间。

(2)的答案：关键路径上的工程是影响总工程进度的关键。

查找关键路径的目的：

辨别哪些是关键工程，以便争取提高关键工程的效率，缩短整个工期。

从上图可以得知，工程V6延迟3天开工，或者延迟3个完成都不会影响项目的工期，所以V6不在关键路径上。

实现思路：

• 假设e(i)表示活动a(i)的最早开始时间，在不推迟整个工程完成的前提下，用l(i)表示活动a(i)的最迟开始时间。两者之差表示完成活动a(i)的时间余量。余量为0的活动就是关键活动，所以连接此活动的2个顶点就是关键路径上的顶点。可以看出，即使提前完成非关键活动，也不能加快工程的进度。

• 辨别关键活动就是要找到e(i) = l(i)的活动。为了求得活动的e(i)和l(i)，首先应求得事件（顶点）的最早发生时间ve(i)和最迟发生时间vl(i)。如果活动a(i)，由边<j, k>表示，其持续时间记为dut(<j, k>),则有如下公式：

  ​ e(i) = ve(i)

  ​ l(i) = vl(k) - dut(<j, k>)

• ve的求法用拓扑排序

• vl的求法用逆拓扑排序

求下图的关键路径

critical_path.h

#ifndef __criticalpath__
#define __criticalpath__

#include <stdio.h>
#include <malloc.h>
#include <assert.h>
#include <memory.h>

#define Default_vertex_size 10

#define T char//dai biao ding dian de lei xing
#define E int
#define MAX_COST 0x7FFFFFFF

typedef struct GraphMtx{
  int MaxVertices;//zui da ding dian shu liang]
  int NumVertices;//shi ji ding dian shu liang
  int NumEdges;//bian de shu lian                                     

  T* VerticesList;//ding dian list
  int** Edge;//bian de lian jie xin xi, bu shi 0 jiu shi 1
}GraphMtx;

//chu shi hua tu
void init_graph(GraphMtx* gm);
//打印二维数组
void show_graph(GraphMtx* gm);
//插入顶点
void insert_vertex(GraphMtx* gm, T v);
//添加顶点间的线
void insert_edge(GraphMtx* gm, T v1, T v2, E cost);
//取得与v顶点有连线的第一个顶点
int getNeighbor(GraphMtx* gm, T v);
//取得与v1顶点，v1顶点之后的v2顶点的之后的有连线的第一个顶点
int getNextNeighbor(GraphMtx* gm, T v1, T v2);

E getWeight(GraphMtx* g, int v1, int v2);
//求解关键路径
void critical_path(GraphMtx* g);

#endif

critical_path.c

#include "critical_path.h"

void init_graph(GraphMtx* gm){
  gm->MaxVertices = Default_vertex_size;
  gm->NumEdges = gm->NumVertices = 0;

  //kai pi ding dian de nei cun kong jian
  gm->VerticesList = (T*)malloc(sizeof(T) * (gm->MaxVertices));
  assert(NULL != gm->VerticesList);

  //创建二维数组
  //让一个int的二级指针，指向一个有8个int一级指针的数组
  //开辟一个能存放gm->MaxVertices个int一级指针的内存空间
  gm->Edge = (int**)malloc(sizeof(int*) * (gm->MaxVertices));
  assert(NULL != gm->Edge);
  //开辟gm->MaxVertices组，能存放gm->MaxVertices个int的内存空间
  for(int i = 0; i < gm->MaxVertices; ++i){
    gm->Edge[i] = (int*)malloc(sizeof(int) * gm->MaxVertices);
  }
  //初始化二维数组
  //让每个顶点之间的边的关系都为不相连的
  for(int i = 0; i < gm->MaxVertices; ++i){
    for(int j = 0; j < gm->MaxVertices; ++j){
      gm->Edge[i][j] = 0;
    }
  }
}
//打印二维数组
void show_graph(GraphMtx* gm){
  printf("  ");
  for(int i = 0; i < gm->NumVertices; ++i){
    printf("%c  ", gm->VerticesList[i]);
  }
  printf("\n");
  for(int i = 0; i < gm->NumVertices; ++i){
    //在行首,打印出顶点的名字
    printf("%c:", gm->VerticesList[i]);
    for(int j = 0; j < gm->NumVertices; ++j){
      printf("%d  ", gm->Edge[i][j]);
    }
    printf("\n");
  }
  printf("\n");
}
//插入顶点
void insert_vertex(GraphMtx* gm, T v){
  //顶点空间已满，不能再插入顶点了
  if(gm->NumVertices >= gm->MaxVertices){
    return;
  }
  gm->VerticesList[gm->NumVertices++] = v;
}

int getVertexIndex(GraphMtx* gm, T v){
  for(int i = 0; i < gm->NumVertices; ++i){
    if(gm->VerticesList[i] == v)return i;
  }
  return -1;
}
//添加顶点间的线
void insert_edge(GraphMtx* gm, T v1, T v2, E cost){
  if(v1 == v2)return;

  //查找2个顶点的下标
  int j = getVertexIndex(gm, v1);
  int k = getVertexIndex(gm, v2);
  //说明找到顶点了,并且点之间还没有线
  if(j != -1 && k != -1 && gm->Edge[j][k] != 1){
    //因为是有方向，所以更新1个值
    gm->Edge[j][k] = cost;
    //边数加一
    gm->NumEdges++;
  }
}
//取得与某顶点有连线的第一个顶点
int getNeighbor(GraphMtx* gm, T v){
  int p = getVertexIndex(gm, v);
  if(-1 == p)return -1;
  for(int i = 0; i < gm->NumVertices; ++i){
    if(gm->Edge[p][i] != 0)
      return i;
  }
  return -1;
}

//取得与v1顶点，v1顶点之后的v2顶点的之后的有连线的第一个顶点
int getNextNeighbor(GraphMtx* gm, T v1, T v2){
  if(v1 == v2)return -1;
  int p1 = getVertexIndex(gm, v1);
  int p2 = getVertexIndex(gm, v2);
  if(p1 == -1 || p2 == -1)return -1;

  for(int i = p2 + 1; i < gm->NumVertices; ++i){
    if(gm->Edge[p1][i] != 0)
      return i;
  }

  return -1;
}

E getWeight(GraphMtx* g, int v1, int v2){
  if(v1 == -1 || v2 == -1)return 0;
  return g->Edge[v1][v2];
}
//求解关键路径
void critical_path(GraphMtx* g){
  int n = g->NumVertices;
  //最早开始时间数组
  int* ve = (int*)malloc(sizeof(int) * n);
  //最晚开始时间数组
  int* vl = (int*)malloc(sizeof(int) * n);
  assert(NULL != ve && NULL != vl);
  for(int i = 0; i < n; ++i){
    ve[i] = 0;
    vl[i] = MAX_COST;
  }

  int j, w;
  //ve
  for(int i = 0; i < n; ++i){
    j = getNeighbor(g, g->VerticesList[i]);
    while(j != -1){
      w = getWeight(g, i, j);
      if(ve[i] + w > ve[j]){
        ve[j] = ve[i] + w;
      }
      j = getNextNeighbor(g,g->VerticesList[i],g->VerticesList[j]);
    }
  }
  //ve  的结果看下图a

  //vl
  vl[n-1] = ve[n-1];
  for(int i = n - 2; i > 0; --i){
    j = getNeighbor(g, g->VerticesList[i]);
    while(j != -1){
      w = getWeight(g, i, j);
      if(vl[j] - w < vl[i]){
        vl[i] = vl[j] - w;
      }
      j = getNextNeighbor(g,g->VerticesList[i],g->VerticesList[j]);
    }
  }
  //vl  的结果看下图b

  int e, l;
  for(int i = 0; i < n; ++i){
    j = getNeighbor(g, g->VerticesList[i]);
    while(j != -1){
      e = ve[i];
      l = vl[j] - getWeight(g, i, j);
      if(e == l){
        printf("<%c, %c>是关键路径\n",g->VerticesList[i],g->VerticesL\
ist[j]);
      }
      j = getNextNeighbor(g,g->VerticesList[i],g->VerticesList[j]);
    }
  }

  free(ve);
  free(vl);
}

图a

图b

critical_path_main.c

#include "critical_path.h"

int main(){
  GraphMtx gm;
  //初始化图
  init_graph(&gm);
  //插入顶点
  insert_vertex(&gm, 'A');
  insert_vertex(&gm, 'B');
  insert_vertex(&gm, 'C');
  insert_vertex(&gm, 'D');
  insert_vertex(&gm, 'E');
  insert_vertex(&gm, 'F');
  insert_vertex(&gm, 'G');
  insert_vertex(&gm, 'H');
  insert_vertex(&gm, 'I');

  //添加连线
  insert_edge(&gm, 'A', 'B', 6);
  insert_edge(&gm, 'A', 'C', 4);
  insert_edge(&gm, 'A', 'D', 5);
  insert_edge(&gm, 'B', 'E', 1);
  insert_edge(&gm, 'C', 'E', 1);
  insert_edge(&gm, 'D', 'F', 2);
  insert_edge(&gm, 'E', 'G', 9);
  insert_edge(&gm, 'E', 'H', 7);
  insert_edge(&gm, 'F', 'H', 4);
  insert_edge(&gm, 'G', 'I', 2);
  insert_edge(&gm, 'H', 'I', 4);
  //打印图
  show_graph(&gm);

  //求解关键路径
  critical_path(&gm);
}

完整代码

编译方法：gcc -g critical_path.c critical_path_main.c