洛谷P1337 [JSOI2004]平衡点 / 吊打XXX(模拟退火)

题目描述

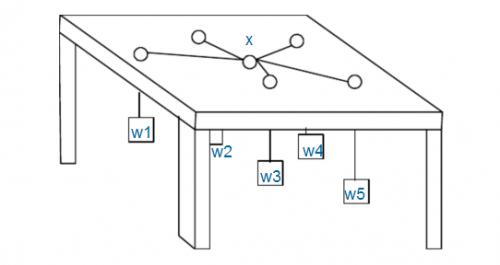
如图：有n个重物，每个重物系在一条足够长的绳子上。每条绳子自上而下穿过桌面上的洞，然后系在一起。图中X处就是公共的绳结。假设绳子是完全弹性的（不会造成能量损失），桌子足够高（因而重物不会垂到地上），且忽略所有的摩擦。

问绳结X最终平衡于何处。

注意：桌面上的洞都比绳结X小得多，所以即使某个重物特别重，绳结X也不可能穿过桌面上的洞掉下来，最多是卡在某个洞口处。

输入输出格式

输入格式：

文件的第一行为一个正整数n（1≤n≤1000），表示重物和洞的数目。接下来的n行，每行是3个整数：Xi.Yi.Wi，分别表示第i个洞的坐标以及第 i个重物的重量。(-10000≤x,y≤10000, 0<w≤1000 )

输出格式：

你的程序必须输出两个浮点数（保留小数点后三位），分别表示处于最终平衡状态时绳结X的横坐标和纵坐标。两个数以一个空格隔开。

输入输出样例

输入样例#1：复制

输出样例#1：复制

0.577 1.000

说明

[JSOI]

居然是道物理题QWQ...

我们所需要求的点，一定是总能量最小的点，这里的总能量，就是每个点的重力势能之和，如果让一个点的重力势能减小，那么拉它的绳子就应该尽量的长，那么在桌面上的绳子就应该尽量的短

因此我们需要求得一个点，使得$\sum_{1}^{n} d[i]*w[i]$最小（$d[i]$表示该到平衡点的距离，$w[i]$表示该点的重量）

这样的话我们显然可以用模拟退火去求这个点

但此题正解并不是模拟退火，

用退火的时候大概有几个需要注意的地方

1.$\Delta T$要设的大一点，

2.移动的距离需要与温度有关

然后无脑退火就可以了

亲测时间种子用19260817可过

#include<cstdio>

#include<cmath>

#include<ctime>

#include<cstdlib>

#define Rand(T) T*( (rand()<<1) - RAND_MAX )

const int MAXN = 1e6 + ;

const double eps = 1e-;

using namespace std;

inline int read() {

    char c = getchar();int x = , f = ;

    while(c < '' || c > '') {if(c == '-') f = -;c = getchar();}

    while(c >= '' && c <= '') {x = x *  + c - '';c = getchar();}

    return x * f;

}

int N;

struct Point {

    double x, y, w;

}a[MAXN];

double AverX,AverY;

double calc(double x,double y) {

    double ans = ;

    for(int i = ; i <= N; i++)

        ans += sqrt((x - a[i].x) * (x - a[i].x) + (y - a[i].y) * (y - a[i].y)) * a[i].w;

    return ans;

}

int main() {

    srand();

    N = read();

    for(int i = ; i <= N; i++)

        scanf("%lf%lf%lf", &a[i].x, &a[i].y, &a[i].w),

        AverX += a[i].x, AverY += a[i].y;

    AverX /= N; AverY /= N;

    double Best = calc(AverX, AverY), BestX = AverX, BestY = AverY;

    double DelatT = 0.98;

    int Time = ;

    while(Time--) {

        double Now = calc(AverX, AverY), NowX = AverX, NowY = AverY;

        for(double T = ; T > eps; T *= DelatT) {

            double Wx = NowX + Rand(T), Wy = NowY + Rand(T);

            double Will = calc(Wx, Wy);

            if(Will < Best) Best = Will, BestX = Wx, BestY = Wy;

            if(Will < Now || ( exp((Will - Now) / T) * RAND_MAX < rand() ))

                Now = Will, NowX = Wx, NowY = Wy;

        }

    }

    printf("%.3lf %.3lf", BestX, BestY);

    return ;

}