Scara机器人微分运动
两关节是Scara的典型结构,其运动学、逆运动学及微分运动计算简单,以下以两关节长度相等为条件进行运动学计算演示,l为杆件1,2长度,杆件1起点为基座零点;
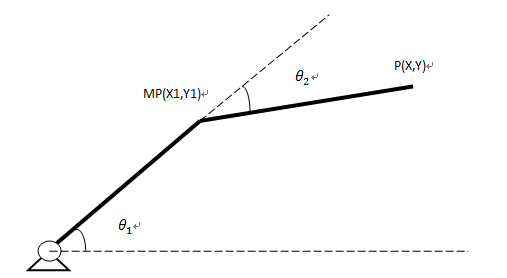
一、 正运动学
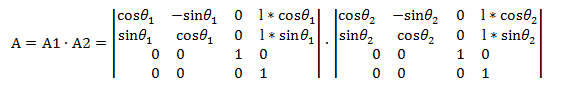
其中位置可描述为:

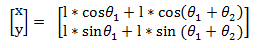
二、 逆运动学
已知当前点P(x,y),求关节1终点MP(x1,y1)
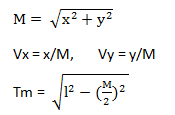
当MP设定在向量(Vx,Vy)逆时针侧:
x1 = x/2 - Tm*Vy y1=y/2 + Tm*Vx
当MP设定在向量(Vx,Vy)顺时针侧:
x1 = x/2 + Tm*Vy y1=y/2 - Tm*Vx
三、 微分运动:
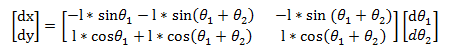
其中雅可比矩阵:

行列式值:
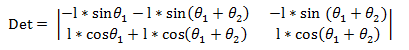
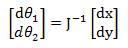

速度(单位向量)矩阵:
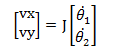
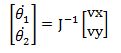
Scara机器人微分运动的更多相关文章
- 【Java】 剑指offer(12) 机器人的运动范围
本文参考自<剑指offer>一书,代码采用Java语言. 更多:<剑指Offer>Java实现合集 题目 地上有一个m行n列的方格.一个机器人从坐标(0, 0)的格子开始移 ...
- 《剑指offer》第十三题(机器人的运动范围)
// 面试题:机器人的运动范围 // 题目:地上有一个m行n列的方格.一个机器人从坐标(0, 0)的格子开始移动,它 // 每一次可以向左.右.上.下移动一格,但不能进入行坐标和列坐标的数位之和 // ...
- Java实现 LeetCode 面试题13. 机器人的运动范围(DFS)
面试题13. 机器人的运动范围 地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] .一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左.右.上.下移动一格(不能移动 ...
- 剑指 Offer 13. 机器人的运动范围 + 深搜 + 递归
剑指 Offer 13. 机器人的运动范围 题目链接 package com.walegarrett.offer; /** * @Author WaleGarrett * @Date 2020/12/ ...
- 剑指 Offer 13. 机器人的运动范围
剑指 Offer 13. 机器人的运动范围 地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] .一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左.右.上.下移动一 ...
- 机器人的运动范围 牛客网 剑指Offer
机器人的运动范围 牛客网 剑指Offer 题目描述 地上有一个m行和n列的方格.一个机器人从坐标0,0的格子开始移动,每一次只能向左,右,上,下四个方向移动一格,但是不能进入行坐标和列坐标的数位之和大 ...
- 安卓手机与ROS通信遥控Gazebo中仿真机器人小车运动(ROS_indigo)
首先,先列出需要用到的一些文件: Gazebo中机器人模型及说明: http://wiki.ros.org/grizzly_simulator https://github.com/g/grizzly ...
- 剑指offer(66)机器人的运动范围
题目描述 地上有一个m行和n列的方格.一个机器人从坐标0,0的格子开始移动,每一次只能向左,右,上,下四个方向移动一格,但是不能进入行坐标和列坐标的数位之和大于k的格子. 例如,当k为18时,机器人能 ...
- 剑指Offer 66. 机器人的运动范围 (回溯)
题目描述 地上有一个m行和n列的方格.一个机器人从坐标0,0的格子开始移动,每一次只能向左,右,上,下四个方向移动一格,但是不能进入行坐标和列坐标的数位之和大于k的格子. 例如,当k为18时,机器人能 ...
随机推荐
- FIN_WAIT_2状态解释
关于网络设备的FIN_WAIT_2状态解释出处:http://hi.baidu.com/netdemon1981/blog/item/584bfbb2aeb1d4acd9335ad9.html 在HT ...
- ios 信任charles https 证书
https://www.charlesproxy.com/documentation/using-charles/ssl-certificates/ https://support.apple.com ...
- 学习python 检测字符串的方法
检测字符串长度的方法:len() 检测字符串是否含有字母的方法:str.isalpha() 检测字符串是否含有数字的方法:str.isnumeric() 检测字符串是否有大写字母:str.upper( ...
- 5.LNMP(Linux + Nginx + MySQL + PHP)环境安装
1.安装Nginx: yum install yum-priorities -y wget http://nginx.org/packages/centos/7/noarch/RPMS/nginx-r ...
- MySQL一般查询日志或者慢查询日志历史数据的清理
general log&slow query log 对于MySQL的一般查询日志和慢查询日志,开启比较简单,其中公用的一个参数是log_output,log_output控制着慢查询和一般查 ...
- 知识点---前端处理支持emoji表情
<!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8&quo ...
- Java Script 简介
Java Script 简介 JavaScript 是世界上最流行的编程语言. 这门语言可用于 HTML 和 web,更可广泛用于服务器.PC.笔记本电脑.平板电脑和智能手机等设备.JavaScrip ...
- Java框架spring 学习笔记(十八):事务管理(xml配置文件管理)
在Java框架spring 学习笔记(十八):事务操作中,有一个问题: package cn.service; import cn.dao.OrderDao; public class OrderSe ...
- 线性筛素数和理解 洛谷P3383
题目链接:https://www.luogu.org/problemnew/show/P3383 线性筛法筛素数的特点是每一个数字只被遍历一次,即时间复杂度为O(n),所以说他是线性的,并且所有的非素 ...
- 记一次win10+oracle11.2安装
下载安装文件,地址:链接:https://pan.baidu.com/s/1gObmWv5_w2Y4Jlf2-RkBYA 密码:1rx9 安装手册参考:链接:https://pan.baidu.com ...
