HanLP二元核心词典解析

本文分析：HanLP版本1.5.3中二元核心词典的存储与查找。当词典文件没有被缓存时，会从文本文件CoreNatureDictionary.ngram.txt中解析出来存储到TreeMap中，然后构造start和pair数组，并基于这两个数组实现词共现频率的二分查找。当已经有缓存bin文件时，那直接读取构建start和pair数组，速度超快。

源码实现

二元核心词典的加载

二元核心词典在文件：CoreNatureDictionary.ngram.txt，约有46.3 MB。程序启动时先尝试加载CoreNatureDictionary.ngram.txt.table.bin 缓存文件，大约22.9 MB。这个缓存文件是序列化保存起来的。

 ObjectInputStream in = new ObjectInputStream(IOUtil.newInputStream(path));

 start = (int[]) in.readObject();

 pair = (int[]) in.readObject();

当缓存文件不存在时，抛出异常：警告: 尝试载入缓存文件E:/idea/hanlp/HanLP/data/dictionary/CoreNatureDictionary.ngram.txt.table.bin发生异常[java.io.FileNotFoundException: 然后解析CoreNatureDictionary.ngram.txt

br = new BufferedReader(new InputStreamReader(IOUtil.newInputStream(path), "UTF-8"));

while ((line = br.readLine()) != null){

    String[] params = line.split("\\s");

    String[] twoWord = params[0].split("@", 2);

    ...

}

然后，使用一个TreeMap<Integer, TreeMap<Integer, Integer>> map来保存解析的每一行二元核心词典条目。

TreeMap<Integer, TreeMap<Integer, Integer>> map = new TreeMap<Integer, TreeMap<Integer, Integer>>();

int idA = CoreDictionary.trie.exactMatchSearch(a);//二元接续的 @ 前的内容

int idB = CoreDictionary.trie.exactMatchSearch(b);//@ 后的内容

TreeMap<Integer, Integer> biMap = map.get(idA);

if (biMap == null){

    biMap = new TreeMap<Integer, Integer>();

    map.put(idA, biMap);//

}

biMap.put(idB, freq);

比如二元接续：“一一@中”，@ 前的内容是：“一一”，@后的内容是 “中”。由于同一个前缀可以有多个后续，比如：

一一@中 1

一一@为 6

一一@交谈 1

所有以 '一一' 开头的 @ 后的后缀以及对应的频率都保存到相应的biMap中：biMap.put(idB, freq);。注意：biMap和map是不同的，map保存整个二元核心词典，而biMap保存某个词对应的所有后缀(这个词 @ 后的所有条目)

map中保存二元核心词典示意图如下：

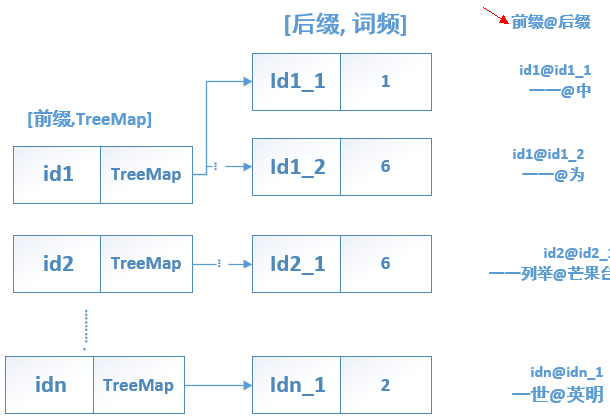
二元核心词典主要由CoreBiGramTableDictionary.java 实现。这个类中有两个整型数组支撑二元核心词典的快速二分查找。

    /**

     * 描述了词在pair中的范围，具体说来<br>

     * 给定一个词idA，从pair[start[idA]]开始的start[idA + 1] - start[idA]描述了一些接续的频次

     */

    static int start[];//支持快速地二分查找

    /**

     * pair[偶数n]表示key，pair[n+1]表示frequency

     */

    static int pair[];

start 数组

首先初始化一个与一元核心词典Trie树 size 一样大小的start 数组：

int maxWordId = CoreDictionary.trie.size();

...

start = new int[maxWordId + 1];

然后，遍历一元核心词典中的词，寻找这些词是是否有二阶共现（或者说：这些词是否存在二元接续）

for (int i = 0; i < maxWordId; ++i){

    TreeMap<Integer, Integer> bMap = map.get(i);

    if (bMap != null){

        for (Map.Entry<Integer, Integer> entry : bMap.entrySet()){

            //省略其他代码

            ++offset;//统计以 这个词 为前缀的所有二阶共现的个数

        }

    }//end if

    start[i + 1] = offset;

}// end outer for loop

if (bMap != null)表示第 i 个词(i从下标0开始)在二元词典中有二阶共现，于是统计以这个词为前缀的所有二阶共现的个数，将之保存到 start 数组中。下面来具体举例，start数组中前37个词的值如下：

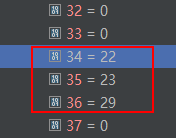
其中start[32]=0，start[33]=0，相应的一元核心词典中的词为 （ ）。即，一个左括号、一个右括号。而这个左括号和右括号在二元核心词典中是不存在词共现的(接续)。也就是说在二元核心词典中没有 （@xxx 这样的条目，也没有 )@xxx 这个条目(xxx 表示任意以 ( 或者 ) 为前缀的后缀接续)。因此，这也是start[32] 和 start[33]=0 都等于0的原因。

部分词的一元核心词典如下：

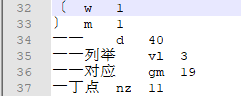
再来看 start[34]=22，start[35]=23。在一元核心词典中，第34个词是"一一"，而在二元核心词典中 '一一'的词共现共有22个，如下：

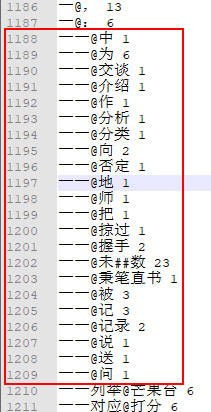
在一元核心词典中，第35个词是 "一一列举"，如上图所示，"一一列举" 在二元核心中只有一个词共现：“一一列举@芒果台”。因此，start[35]=22+1=23。从这里也可以看出：

给定一个词idA，从pair[start[idA]]开始的start[idA + 1] - start[idA]描述了一些接续的频次

比如，idA=35，对应词“一一列举”，它的接续频次为1，即：23-22=1

这样做的好处是什么呢？自问自答一下：^~，就是大大减少了二分查找的范围。

pair 数组

pair数组的长度是二元核心词典行数的两倍

int total = 0;

while ((line = br.readLine()) != null){

    //省略其他代码

    total += 2;

}

pair数组偶数下标存储保存的是一元核心词典中的词的下标，而对应的偶数加1 处的下标存储这个词的共现频率。即： pair[偶数n]表示key，pair[n+1]表示frequency

            pair = new int[total];  // total是接续的个数*2

            for (int i = 0; i < maxWordId; ++i)

            {

                TreeMap<Integer, Integer> bMap = map.get(i);//i==0?

                if (bMap != null)//某个词在一元核心词典中, 但是并没有出现在二元核心词典中(这个词没有二元核心词共现)

                {

                    for (Map.Entry<Integer, Integer> entry : bMap.entrySet())

                    {

                        int index = offset << 1;

                        pair[index] = entry.getKey();//词 在一元核心词典中的id

                        pair[index + 1] = entry.getValue();//频率

                    }

                }

            }

举例来说：对于 '一一@中'，pair数组是如何保存这对词的词共现频率的呢？

'一一'在 map 中第0号位置处，它是一元核心词典中的第34个词。 共有22个共现词。如下：

其中，第一个共现词是 '一一 @中'，就是'一一'与 '中' 共同出现，出现的频率为1。而 ''中'' 在一元核心词典中的 4124行，如下图所示：

因此，'一一@中'的pair数组存储如下：

0=4123 （‘中’在一元核心词典中的位置（从下标0开始计算））

1=1 （'一一@中'的词共现频率）

2=5106 （'为' 在一元核心词典中的位置）【为 p 65723】

3=6 ('一一@为'的词共现频率)

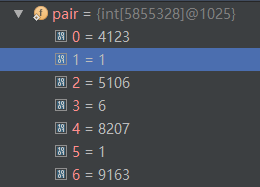
由此可知，对于二元核心词典共现词而言，共同前缀的后续词在 pair数组中是顺序存储的，比如说：前缀'一一'的所有后缀：中、为、交谈……按顺序依次在 pair 数组中存储。而这也是能够对 pair 数组进行二分查找的基础。

一一@中 1

一一@为 6

一一@交谈 1

一一@介绍 1

一一@作 1

一一@分析

.......//省略其他

二分查找

现在来看看二分查找是干什么用的？为什么减少了二分查找的范围。为了获取某两个词（idA 和 idB）的词共现频率，需要进行二分查找：

public static int getBiFrequency(int idA, int idB){

    //省略其他代码

    int index = binarySearch(pair, start[idA], start[idA + 1] - start[idA], idB);

    return pair[index + 1];

}

根据前面介绍，start[idA + 1] - start[idA]就是以 idA 为前缀的所有词的词共现频率。比如，以 '一一' 为前缀的词一共有22个，假设我要查找 '一一@向' 的词共现频率是多少？在核心二元词典文件CoreNatureDictionary.ngram.txt中，我们知道 '一一@向' 的词共现频率为2，但是：如何用程序快速地实现查找呢？

二元核心词典的总个数还是很多的，比如在HanLP1.5.3大约有290万个二元核心词条，如果每查询一次 idA@idB 的词共现频率就要从290万个词条里面查询，显然效率很低。若先定位出所有以 idA 为前缀的共现词：idA@xx1，idA@xx2，idA@xx3……，然后再从从这些 以idA为前缀的共现词中进行二分查找，来查找 idA@idB，这样查找的效率就快了许多。

而start 数组保存了一元词典中每个词在二元词典中的词共现情况： start[idA] 代表 idA在 pair 数组中共现词的起始位置，而start[idA + 1] - start[idA]代表以idA 为前缀的共现词一共有多少个，这样二分查找的范围就只在 start[idA] 和 start[idA] + (start[idA + 1] - start[idA]) - 1之间了。

    private static int binarySearch(int[] a, int fromIndex, int length, int key)

    {

        int low = fromIndex;

        int high = fromIndex + length - 1;

        //省略其他代码

说到这里，再多说一点：二元核心词典的二分查找是为了获取 idA@idB 的词共现频率，而这个词共现频率的用处之一就是最短路径分词算法(维特比分词)，用来计算最短路径的权重。关于最短路径分词，可参考这篇解析：

//只列出关键代码

List<Vertex> vertexList = viterbi(wordNetAll);//求解词网的最短路径

to.updateFrom(node);//更新权重

double weight = from.weight + MathTools.calculateWeight(from, this);//计算两个顶点(idA->idB)的权重

int nTwoWordsFreq = CoreBiGramTableDictionary.getBiFrequency(from.wordID, to.wordID);//查核心二元词典

int index = binarySearch(pair, start[idA], start[idA + 1] - start[idA], idB);//二分查找 idA@idB共现频率

总结

有时候由于特定项目需要，需要修改核心词典。比如添加一个新的二元词共现词条到二元核心词典中去，这时就需要注意：添加的新词条需要存在于一元核心词典中，否则添加无效。另外，添加到CoreNatureDictionary.ngram.txt里面的二元共现词的位置不太重要，因为相同的前缀共现词都会保存到同一个TreeMap中，但是最好也是连续放在一起，这样二元核心词典就不会太混乱。

参考：HanLP用户自定义词典源码分析

原文：http://www.cnblogs.com/hapjin/p/9010504.html