LOJ #2541「PKUWC2018」猎人杀

这样$ PKUWC$就只差一道斗地主了

假装补题补完了吧.....

这题还是挺巧妙的啊......

LOJ # 2541

---

题意

每个人有一个嘲讽值$a_i$，每次杀死一个人，杀死某人的概率为$ \frac{a_i}{a_{alive}}$，求第一个人最后死的概率

数据范围：$ 1 \leq a_i \leq 10^5，\sum\limits_{i=1}^n a_i \leq 10^5$

---

$Solution$

以下部分用$ val$表示所有人的嘲讽值之和

先讲讲$ n*val$的$ DP$

用$ P_S$表示集合$ S$中的人都在$ 1$后面死的概率

由于期间打死其他人不会影响$ P_S$的结果

每个$ P_S$是独立的

等价与下一枪打在$ S$或$1$上打死$1$的概率即$ \frac{a_i}{a_S+a_i}$

其中$ a_S$表示集合$ S$的嘲讽值之和

则容斥计算答案为$ \sum\limits(-1)^{|S|+1}P_S$

容易发现枚举集合的复杂度过大无法承受

发现$ val$不大

尝试用$ f_{i,j}$表示前$ i$个人(从2开始枚举)嘲讽值之和为$ j$的方案数

发现有容斥系数不能直接记录方案

不过没有关系，由于容斥系数只和奇偶性有关，我们只需要把$ f_{i,j}$改成嘲讽值之和为$j$的系数和即可

转移的时候分选$ i$和不选$i$两种

如果选了前面的奇偶性会全部改变

因此得出转移方程式$ f_{i,j}=f_{i-1,j}-f_{i-1,j-a[i]}$

可以过$ 50$分

---

考虑生成函数

发现转移的本质是若干个形如$ (1-x^{a_i})$的二项式相乘

即最终转移结果为 $\prod\limits_{i=2}^n 1-x^{a_i}$

用$ NTT$分治计算这个过程

由于类似线段树结构的分治只有$ log_n$层，每层的复杂度是$ O(val \ log_{val})$

因此总复杂度是$ O(val \ log_n \  log_{val})$的，可以通过本题

以及还有$一个log$的小$ trick$

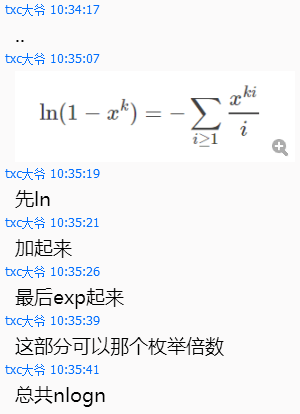
暂时还不会....以后再写吧

$update$

尝试去写了一下，好像比$ log^2$的分治慢啊....代码太丑就不贴了...Exp常数真大...

---

$ my \ code:$

#include<ctime>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<queue>
#define p 998244353
#define rt register int
#define ll long long
using namespace std;
inline ll read(){
    ll x = ; char zf = ; char ch = getchar();
    while (ch != '-' && !isdigit(ch)) ch = getchar();
    if (ch == '-') zf = -, ch = getchar();
    while (isdigit(ch)) x = x *  + ch - '', ch = getchar(); return x * zf;
}
void write(ll y){if(y<)putchar('-'),y=-y;if(y>)write(y/);putchar(y%+);}
void writeln(const ll y){write(y);putchar('\n');}
int i,j,k,m,n,x,y,z,cnt;
int a[];
int ksm(int x,int y){
    int ans=;
    for(rt i=y;i;i>>=,x=1ll*x*x%p)if(i&)ans=1ll*ans*x%p;
    return ans;
}
namespace poly{
    vector<int>R;
    void getR(int n){
        R.resize(n);
        for(rt i=;i<n;i++)R[i]=(R[i>>]>>)|(i&)*(n>>);
    }
    void NTT(int n,vector<int>&A,int fla){
        for(rt i=;i<n;i++)if(i>R[i])swap(A[i],A[R[i]]);
        for(rt i=;i<n;i<<=){
            int w=ksm(,(p-)//i);
            for(rt j=;j<n;j+=i<<){
                int K=;
                for(rt k=;k<i;k++,K=1ll*K*w%p){
                    int x=A[j+k],y=1ll*K*A[i+j+k]%p;
                    A[j+k]=(x+y)%p,A[i+j+k]=(x-y)%p;
                }
            }
        }
        if(fla==-){
            reverse(A.begin()+,A.end());int invn=ksm(n,p-);
            for(rt i=;i<n;i++)A[i]=1ll*A[i]*invn%p;
        }
    }
}
using namespace poly;
int calc(int L,int R,vector<int>&A){
    if(L==R){
        A.resize(a[L]+);
        A[]=;A[a[L]]=-;
        return a[L];
    }
    const int mid=L+R>>;
    vector<int>f,g;
    int len=calc(L,mid,f)+calc(mid+,R,g);
    int lim=;while(lim<=len)lim<<=;
    getR(lim);f.resize(lim);g.resize(lim);A.resize(lim);
    NTT(lim,f,);NTT(lim,g,);
    for(rt i=;i<lim;i++)A[i]=1ll*f[i]*g[i]%p;
    NTT(lim,A,-);
    return len;
}
int main(){
    n=read();
    for(rt i=;i<=n;i++)a[i]=read();
    vector<int>xs;
    int sum=calc(,n,xs);int ans=;
    for(rt i=;i<=sum;i++)(ans+=1ll*xs[i]*ksm(i+a[],p-)%p*a[]%p)%=p;
    cout<<(ans+p)%p;
    return ;
}