uva 10609 - Fractal

题目大意：给出A，B两个点的坐标，以及T，每次找到A、B的四等分点C，D，然后以AB/2为边长，C,D为顶点，构建一个等边三角形，E为另外一个顶点，然后再对C，E；E，D做同样的操作，直到构建的等边三角形的边长小于T时。输出所有过程中的点，按照x坐标排序，相同的按照y坐标。

解题思路：dfs模拟，用ans记录点，最后排序，C，D，E可以根据向量的方法从A，B得到。

 #include <cstdio>
 #include <vector>
 #include <cmath>
 #include <altorithm>
 using namespace std;
 const double sq3 = sqrt(3.0);
 struct point {
     double x, y;
 };
 
 vector<point> ans;
 double T;
 
 bool cmp (const point& A, const point& B)
 {
     if(fabs(A.x - B.x) > 1e-) return A.x < B.x;
     return A.y < B.y;
 }
 
 double dis(double x, double y) { return sqrt(x * x + y * y); }
 
 void dfs (point A, point B)
 {
     double len = dis(A.x - B.x, A.y - B.y);
     if (len /  < T) return;
 
     point C, D, E;
 
     C.x = B.x +  * (A.x - B.x) / ;
     C.y = B.y +  * (A.y - B.y) / ;
 
     D.x = B.x + (A.x - B.x) / ;
     D.y = B.y + (A.y - B.y) / ;
 
     E.x = (A.x + B.x)/ + sq3/*(A.y - B.y);
     E.y = (A.y + B.y)/ - sq3/*(A.x - B.x);
 
     ans.push_back(C);
     ans.push_back(D);
     ans.push_back(E);
 
     dfs(C, E);
     dfs(E, D);
 }
 
 int main()
 {
     int cas = ;
     point A, B;
     while(scanf("%lf%lf%lf%lf%lf", &A.x, &A.y, &B.x, &B.y, &T) ==  && T >= )
     {
         ans.clear();
         ans.push_back(A);
         ans.push_back(B);
 
         dfs(A, B);
 
         printf("Case %d:\n", cas ++);
         sort(ans.begin(), ans.end(), cmp);
         printf("%lu\n", ans.size());
         for (int i = ; i < ans.size(); i++)
             printf("%0.5lf %0.5lf\n", ans[i].x, ans[i].y);
     }
     return ;
 }

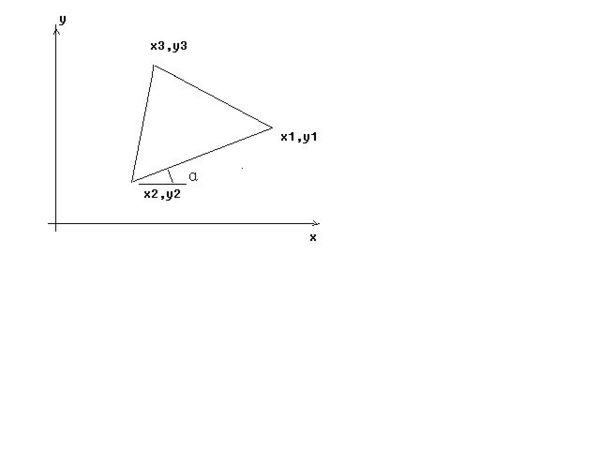
已知等边三角形两点的坐标.求第三点坐标, 已知X(x1,y1), Y(x2,y2) 求Z(x3,y3), x3=? y3=?

1、求已知线段的斜角：tgα=(y1-y2)/(x1-x2) 
2、求已知线段的长度：L=√((y1-y2)^2+(x1-x2)^2)
3、求第三点的坐标：
    x3=x2+L*cos(α+60)；y3=y2+L*sin(α+60)