poj2409 Let it Bead

                                                                  Let it Bead

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 5397		Accepted: 3609

Description

"Let it Bead" company is located upstairs at 700 Cannery Row in Monterey, CA. As you can deduce from the company name, their business is beads. Their PR department found out that customers are interested in buying colored bracelets. However, over 90 percent of the target audience insists that the bracelets be unique. (Just imagine what happened if two women showed up at the same party wearing identical bracelets!) It's a good thing that bracelets can have different lengths and need not be made of beads of one color. Help the boss estimating maximum profit by calculating how many different bracelets can be produced.

A bracelet is a ring-like sequence of s beads each of which can have one of c distinct colors. The ring is closed, i.e. has no beginning or end, and has no direction. Assume an unlimited supply of beads of each color. For different values of s and c, calculate the number of different bracelets that can be made.

Input

Every line of the input file defines a test case and contains two integers: the number of available colors c followed by the length of the bracelets s. Input is terminated by c=s=0. Otherwise, both are positive, and, due to technical difficulties in the bracelet-fabrication-machine, cs<=32, i.e. their product does not exceed 32.

Output

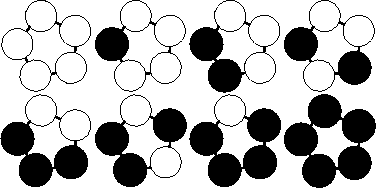For each test case output on a single line the number of unique bracelets. The figure below shows the 8 different bracelets that can be made with 2 colors and 5 beads.

Sample Input

1 1
2 1
2 2
5 1
2 5
2 6
6 2
0 0

Sample Output

1
2
3
5
8
13
21

题意：每次给你m种颜色，n个珠子要成一个环，可以翻转也可以旋转，要问本质不同的染色方案有几种

首先，对于每次旋转i，循环节一定是有gcd（i,n）个，首先，如果对于一个串一直旋转i的长度，那么回到最初的时候一定是旋转了 lcm（i，n）/i 次，那么任意一个节点，一定经过了lcm(i,n)/i个节点，那么这么多个节点，都是等价类E，由于环上每个等价类的元素数量都相等，所以循环节个数为 n*i/(lcm(i,n)=gcd(i,n)

到这里为止，旋转的情况我们已经考虑过了，我们再考虑一下翻转的情况：
 对于奇数，翻转情况只有一个点，和它对面的中点作为对称轴，一共n种，循环节为n/2+1

 对于偶数，有两种情况，一个是两个对称点构成对称轴，n/2种，循环节为n/2+1
                      一个是两个中点构成对称轴，也是n/2种，循环节为n/2
综上，所有的置换总数有2*n种，这时候我们只需要利用polay计数就可以AC了

2016-06-10:PKUSC居然考了这题，TAT还好有学过。。

 #include<algorithm>
 #include<cstdio>
 #include<cmath>
 #include<cstring>
 #include<iostream>
 #define ll long long
 int n,m;
 int Pow(int x,int y){
     int res=;
     while (y){
         if (y%) res*=x;
         x*=x;
         y/=;
     }
     return res;
 }
 int gcd(int a,int b){
     if (b==) return a;
     else return gcd(b,a%b);
 }
 int main(){
     while (scanf("%d%d",&m,&n)!=EOF){
         if (n==&&m==) return ;
         int ans=;
         for (int i=;i<n;i++)
          ans+=Pow(m,gcd(i,n));
         if (n%){
             ans+=n*Pow(m,(n/)+);
             ans/=*n;
             printf("%d\n",ans);
         }else{
             ans+=n/*Pow(m,(n/)+);
             ans+=n/*Pow(m,n/);
             ans/=*n;
             printf("%d\n",ans);
         }
     }
 }