用BFS和DFS解决圆盘状态搜索问题

人工智能课程的实验（我的解法其实更像是算法课程的实验）

用到的算法：深度优先搜索、宽度优先搜索（状态扩展的不同策略）

数据结构：表示状态的结构体、多维数组

（可能是最近做算法竞赛题的影响，这次并不像以前那样依赖类和面向对象了，而是用最简单（几乎没有封装）的数据表示方法和大量的全局变量来存储数据，用面向过程的写法，以快速解决某一问题为目的设计程序。安全性和可扩展性势必降低，有些技巧的使用也让代码变得难懂；但是代码简洁，节省运行的时间和空间开销，这应该就是算法竞赛更加看重的吧）

这次用了C++写了控制台版，打印状态三元组；又用C#写了图形界面版，打印出圆盘的状态。

二者的算法是完全一致的，执行结果也一致，只是语法和输出的一些处理不同。

下面是运行结果截图，以深度优先为例

 

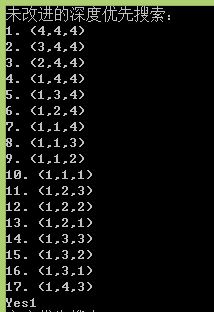
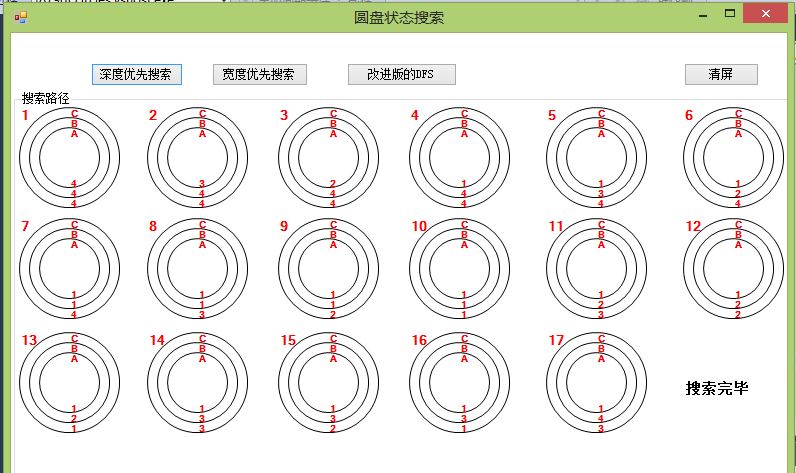
下面以C++版为例介绍实现

结构体和全局变量的定义

 struct State
  {
      int a, b, c;//表示圆盘朝南方向的数字
      State(){}
      State(int na, int nb, int nc) :a(na), b(nb), c(nc){}
  };

  int vis[][][];//用来记录每个状态是否被访问过
  int num;//用来记录第几个状态

DFS（用栈实现）

 int dfs()
 {
     stack<State> sta;
     sta.push(State(,,));
     vis[][][] = ;
     while (sta.size())
     {
         State cur = sta.top();
         sta.pop();
         cout << ++num << ". ("<<cur.a<<","<<cur.b<<","<<cur.c<<")"<<endl;
         if (cur.a ==  && cur.b ==  && cur.c == )
             return ;//命中
         if (cur.c - > && vis[cur.a][cur.b][cur.c-] == )
         {
             vis[cur.a][cur.b][cur.c-] = ;
             sta.push(State(cur.a, cur.b, cur.c-));
         }
         if (cur.b - > && vis[cur.a][cur.b-][cur.c] == )
         {
             vis[cur.a][cur.b-][cur.c] = ;
             sta.push(State(cur.a, cur.b-, cur.c));
         }
         if (cur.a - > && vis[cur.a-][cur.b][cur.c] == )
         {
             vis[cur.a-][cur.b][cur.c] = ;
             sta.push(State(cur.a-, cur.b, cur.c));
         }
     }
     return ;
 }

BFS（用队列实现）

 int bfs()
 {
     queue<State> que;
     que.push(State(, , ));
     vis[][][] = ;
     while (que.size())
     {
         State cur = que.front();
         que.pop();

         cout << ++num << ". ("<<cur.a<<","<<cur.b<<","<<cur.c<<")"<<endl;
         if (cur.a ==  && cur.b ==  && cur.c == )
             return ;//命中
         if (cur.a - > && vis[cur.a - ][cur.b][cur.c] == )
         {
             vis[cur.a-][cur.b][cur.c] = ;
             que.push(State(cur.a-, cur.b, cur.c));
         }
         if (cur.b - > && vis[cur.a][cur.b - ][cur.c] == )
         {
             vis[cur.a][cur.b-][cur.c] = ;
             que.push(State(cur.a, cur.b-, cur.c));
         }
         if (cur.c - > && vis[cur.a][cur.b][cur.c - ] == )
         {
             vis[cur.a][cur.b][cur.c-] = ;
             que.push(State(cur.a, cur.b, cur.c-));
         }
     }
     return ;
 }

　　你会发现DFS和BFS的不同仅在于对某一状态（节点）进行扩展时，其兄弟结点被暂存的顺序。这个顺序决定了节点扩展的顺序，即将“树”这样的“半线性结构”转化为“线性结构”的不同策略。

　　因为这两种搜索策略都是从一开始就知道要对每一个未命中的节点进行怎样的处理，即搜索过程中产生的结果对搜索策略没有影响，所以这两种都属于“盲目式搜索”。相对而言，人工智能领域发展出“启发式搜索”，即在进行待扩展节点的选取时，要根据一个“估价函数”来选取“最有希望”的节点分支进行下一步扩展。

老师的习题解析中对DFS进行了改进，在扩展某个节点时判断的是它的子节点，这样可以尽早找到目标。个人认为这相当于在局部做了广度优先。

改进后的访问过的状态由17个降到5个，但其实加上判断过又未命中的兄弟节点，是降到了11个。如下

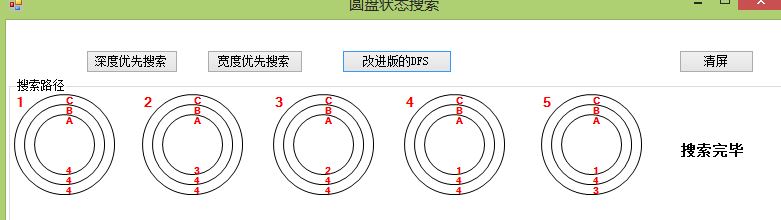
改进版DFS的代码

 int dfs_a()
 {
     stack<State> sta;
     sta.push(State(,,));
     vis[][][] = ;
     while (sta.size())
     {
         State cur = sta.top();
         sta.pop();
         cout << ++num << ". ("<<cur.a<<","<<cur.b<<","<<cur.c<<")"<<endl;

         if (cur.c - > && vis[cur.a][cur.b][cur.c-] == )
         {
             vis[cur.a][cur.b][cur.c-] = ;
             if (cur.a ==  && cur.b ==  && cur.c- == )
             {
                 cout << ++num << ". ("<<cur.a<<","<<cur.b<<","<<cur.c-<<")"<<endl;
                 return ;//命中
             }
             sta.push(State(cur.a, cur.b, cur.c-));
         }
         if (cur.b - > && vis[cur.a][cur.b-][cur.c] == )
         {
             vis[cur.a][cur.b-][cur.c] = ;
             if (cur.a ==  && cur.b- ==  && cur.c == )
             {
                 cout << ++num << ". ("<<cur.a<<","<<cur.b-<<","<<cur.c<<")"<<endl;
                 return ;//命中
             }
             sta.push(State(cur.a, cur.b-, cur.c));
         }
         if (cur.a - > && vis[cur.a-][cur.b][cur.c] == )
         {
             vis[cur.a-][cur.b][cur.c] = ;
             if (cur.a- ==  && cur.b ==  && cur.c == )
             {
                 cout << ++num << ". ("<<cur.a-<<","<<cur.b<<","<<cur.c<<")"<<endl;
                 return ;//命中
             }
             sta.push(State(cur.a-, cur.b, cur.c));
         }
     }
     return ;
 }

以上就是算法的内容。

关于C#图形界面的实现，也很简单。下面是显示每个圆盘状态的函数

 //打印状态函数
         private void print_circle(State st,int num)
         {
             Thread.Sleep();
             Graphics gra = this.groupBox1.Controls[num-].CreateGraphics();//指定第num个圆盘显示

             gra.SmoothingMode = System.Drawing.Drawing2D.SmoothingMode.AntiAlias;

             Pen pen = new Pen(Color.Black);//画笔颜色                                

             gra.DrawEllipse(pen, , , , );//画圆的方法，x坐标、y坐标、宽、高
             gra.DrawEllipse(pen, , , , );
             gra.DrawEllipse(pen, , , , );

             Font font1 = new Font("", , FontStyle.Bold);
             Font font2 = new Font("", , FontStyle.Bold);
             Brush bush = new SolidBrush(Color.Red);//字填充的颜色
             gra.DrawString(num + "", font2, bush, , );
             gra.DrawString("A", font1, bush, , );
             gra.DrawString("B", font1, bush, , );
             gra.DrawString("C", font1, bush, , );
             gra.DrawString(st.a+"", font1, bush, , );
             gra.DrawString(st.b+"", font1, bush, , );
             gra.DrawString(st.c+"", font1, bush, , );
         }

关于界面的设计，预先放好足够多的picturebox，将它们放入一个groupbox里，然后根据传递进来的参数找特定的picturebox画图。

　　在遍历groupbox时，我发现里面元素的顺序如果不是按顺序拖入的，会非常错乱。。。由于很菜鸟，我百度了很久都没有找到直接修改内部顺序的方法，只好打开groupbox的定义代码，调整添加元素函数的顺序才得以重排。

　　以上是我对这个圆盘问题的求解。

　　在检查实验时，老师说这个问题更通用的抽象是一个5个参数的“搜索机”，5个参数分别为：初始状态集合、目标状态集合、初始状态、目标状态、状态转移函数。（百度后发现好像图灵机的模型）这种方法需要在一开始生成所有可能状态。相比我的“动态生成状态”策略，这样势必会增加空间开销，但在搜索次数多时可以节省重复生成状态的时间，两种方法各有千秋吧。后一种方法更切合现在学习人工智能课的“状态空间搜索”思想。