uva-699 Not so Mobile (杠杆，巧妙递归)

  Not so Mobile 

Before being an ubiquous communications gadget, a mobile was just a structure made of strings and wires suspending colourfull things. This kind of mobile is usually found hanging over cradles of small babies.

 

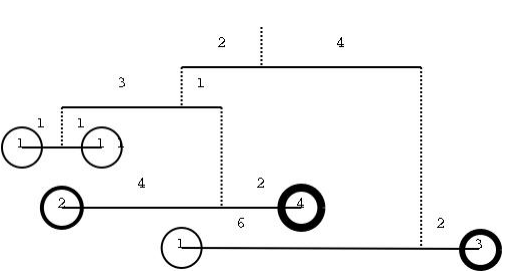
The figure illustrates a simple mobile. It is just a wire, suspended by a string, with an object on each side. It can also be seen as a kind of lever with the fulcrum on the point where the string ties the wire. From the lever principle we know that to balance a simple mobile the product of the weight of the objects by their distance to the fulcrum must be equal. That isW_l×D_l = W_r×D_r where D_l is the left distance, D_r is the right distance, W_l is the left weight and W_r is the right weight.

In a more complex mobile the object may be replaced by a sub-mobile, as shown in the next figure. In this case it is not so straightforward to check if the mobile is balanced so we need you to write a program that, given a description of a mobile as input, checks whether the mobile is in equilibrium or not.

Input

The input begins with a single positive integer on a line by itself indicating the number of the cases following, each of them as described below. This line is followed by a blank line, and there is also a blank line between two consecutive inputs.

The input is composed of several lines, each containing 4 integers separated by a single space. The 4 integers represent the distances of each object to the fulcrum and their weights, in the format: W_l D_l W_r D_r

If W_l or W_r is zero then there is a sub-mobile hanging from that end and the following lines define the the sub-mobile. In this case we compute the weight of the sub-mobile as the sum of weights of all its objects, disregarding the weight of the wires and strings. If both W_l and W_r are zero then the following lines define two sub-mobiles: first the left then the right one.

Output

For each test case, the output must follow the description below. The outputs of two consecutive cases will be separated by a blank line.

Write `YES' if the mobile is in equilibrium, write `NO' otherwise.

Sample Input

1

0 2 0 4
0 3 0 1
1 1 1 1
2 4 4 2
1 6 3 2

Sample Output

YES
题解：题意是让求这个杠杆是不是平衡；看了大神的代码，处理的很巧妙，如果当前质量是0，递归输入子天平，每个子天平判断是否平衡，就可以了；
代码：

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<queue>
using namespace std;
#define SI(x) scanf("%d",&x)
#define mem(x,y) memset(x,y,sizeof(x))
#define PI(x) printf("%d",x)
#define P_ printf(" ")
const int INF=0x3f3f3f3f;
typedef long long LL;
bool solve(int &w){
	int w1,d1,w2,d2;
	scanf("%d%d%d%d",&w1,&d1,&w2,&d2);
	int temp1=true,temp2=true;
	if(!w1)temp1=solve(w1);
	if(!w2)temp2=solve(w2);
	w=w1+w2;
	if(w1*d1==w2*d2&&temp1&&temp2)return true;
	else return false;
}
int main(){
	int T;
	SI(T);
	while(T--){
		int w;
		if(solve(w))puts("YES");
		else puts("NO");
		if(T)puts("");
	}
	return 0;
}