Code Festival 2017 Qual B E Popping Balls

传送门

神仙计数！

我的计数真的好差啊= =

不过这个题真的神仙

看了题解把整个过程在草稿纸上重写了一遍才想明白= =（一张草稿纸就没有了！！！）

计数的关键就是在于 枚举的有效性和独立性【不能重复计数】

然后我们就来思考一下这个题

1. 确定t

我们重定义t为第一个取出的蓝球的位置

那么t的选择区间是[1,a+1] 分别对应[a+1,1]的时候取出

枚举区间：[1,a+1]

2.枚举i

取走前面的 a+1-t个 红球 和 在位置t的 1个 蓝球（根据第一步的定义）

这个时候总共取出了 a-t+2个 球 还没有取的有 b-1个 蓝球 和 t-1个 红球

我们发现现在红球和蓝球可以任意排列 因为t所在的位置开始全部都是蓝球 而1开始全部都是红球

这样计数不会重复因为最开始枚举的t保证了前面取出的已经不同

此时我们枚举i表示取走的蓝球数量

我们的可以任取几个球呢？ 答案是 b-1个 因为t所在的位置在球数<t的时候就失效了 所以 b+t-2-(t-1)=b-1

所以i的枚举区间是[0,b-1]

这时候的贡献 : C(i,b-1)

考虑现在剩下的球的个数 有 t-1-i个 红球 和 i个蓝球

3.确定s

这时候我们的t已经失效了 并且已知了前面的互不相同的序列

s的枚举范围与t类似 这个时候s表示现在开始第一个取蓝球的位置

和第一步同理 表示先取 t-i-s个 红球再取 1个 蓝球

枚举区间：[1,t-i]

4.枚举j

考虑此时剩下了 s-1个 红球 和 i-1个 蓝球

此时位置s开始全是蓝球 1位置全是红球 又可以任选啦=v=

我们考虑枚举j表示 取出 j个 红球 和 i-1-j个 蓝球

这个的贡献就是：C(j,i-1)

枚举区间对应的是[0,min(s-1,i-1)]

于是我们现在按照这个做得到了一个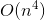的枚举大法

接着考虑优化 首先j一定是可以对应一个前缀和的当然就是f[i-1][s-1]

s的枚举也是可以用前缀和优化掉的 就是对f进行前缀和得到sum[i-1][t-i-1]（注意细节i可以取到0所以要每次枚举t的时候++）

然后这样的话我们就得到了一个非常优秀的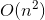做法

这样就是可以通过的啦=v=

完结撒花~

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define inf 20021225
#define ll long long
#define N 2000
#define mdn 1000000007
using namespace std;

int f[N+10][N+10],sum[N+10][N+10],C[N+10][N+10];

void prework()
{
	C[0][0]=C[1][0]=C[1][1]=1;
	//f[0][0]=sum[0][0]=1;
	for(int i=2;i<=N+1;i++)
	{
		C[i][0]=C[i][i]=1;
		for(int j=1;j<i;j++)	C[i][j]=(C[i-1][j-1]+C[i-1][j])%mdn;
	}
	for(int i=0;i<=N+1;i++)
	{
		f[i][0] = C[i][0];
		for(int j=1;j<=N+1;j++)
			f[i][j] = (f[i][j-1] + C[i][j])%mdn;
	}
	for(int i=0;i<=N+1;i++)
	{
		sum[i][0] = f[i][0];
		for(int j=1;j<=N+1;j++)
			sum[i][j]=(sum[i][j-1] + f[i][j])%mdn;
	}
}
int a,b;
void work()
{
	int ans=0;
	prework();
	for(int t=1;t<=a+1;t++)
	{
		ans++;
		for(int i=1;i<=min(t-1,b-1);i++)
		{
			ans += (ll)C[b-1][i]*sum[i-1][t-i-1]%mdn;
			ans %= mdn;
		}
	}
	printf("%d\n",ans);
}

int main()
{
	scanf("%d%d",&a,&b);
	work();
	return 0;
}