[CSP-S模拟测试]:毛一琛（meet in the middle）

题目描述

　　历史学考后，$MYC$和$ztr$对答案，发现选择题他们没有一道选的是一样的。最后他们都考了个$C$。现在问题来了，假设他们五五开，分数恰好一样（问答题分数也恰好一样，只考虑选择题）。已知考题是$N$道选择题（第$i$题分数为$M(i)$）。问$ztr$和$MYC$做对的题的并有多少种可能？众所周知，历史学考选择题有$25$题，但是$MYC$为了给你降低难度，$n$不超过$20$。
　　一句话题意：有多少个非空子集，能划分成和相等的两份。

原题见：$USACO\ 2012\ OPEN\ GOLD\ subsets$

---

输入格式

第一行：整数$N$
第$2..1+N$行：第$i+1$行是$M(i)$

---

输出格式

一个整数表示答案

---

样例

样例输入：

4
1
2
3
4

样例输出：

3

---

数据范围与提示

样例解释：

有三个合法的集合：$\{1,2,3\}$，它可以被分割成$\{1,2\}$和$\{3\}$，集合$\{1,3,4\}$，它可以被分割为$\{1,3\}$和$\{4\}$；集合$\{1,2,3,4\}$可以被分割成子集$\{1,4\}$和$\{2,3\}$。

数据范围：

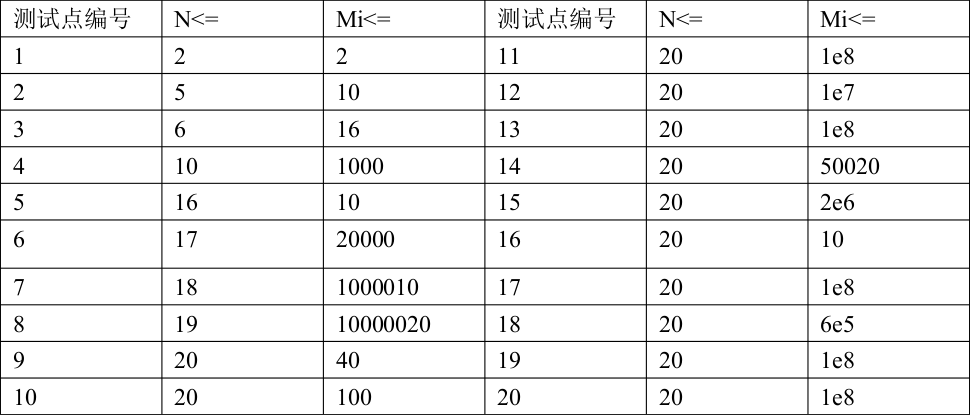
不要问我为什么数据范围这么奇怪。。。因为要给大家送分。。。

---

题解

又被题意坑死……

先来解释一下题意，题目是要统计所有子集中可以被等分的集合（如果有多种方案，不能重复统计）。

$\Theta(n^3)$暴力应该都会打（分为不选，给一个人，给另一个人）。

但是这样显然过不去，考虑$meet\ in\ the\ middle$，先枚举左边$3^{\frac{N}{2}}$，再枚举右边$3^{\frac{N}{2}}$即可。

时间复杂度：$\Theta(6^{\frac{N}{2}})$。、

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
const int mod=30000019;
struct rec{int nxt,to,now,val;}e[59050];
int head[300000019],cnt;
int N;
int a[21];
bool vis[1100][1100],v[21];
int ans;
void insert(int now,int val)
{
	int key=(val%mod+mod)%mod;
	for(int i=head[key];i;i=e[i].nxt)
		if(e[i].now==now&&e[i].val==val)return;
	e[++cnt].nxt=head[key];
	e[cnt].now=now;
	e[cnt].val=val;
	head[key]=cnt;
}
int ask(int now,int val)
{
	int key=(val%mod+mod)%mod,res=0;
	for(int i=head[key];i;i=e[i].nxt)
		if(e[i].val==val&&!vis[e[i].now][now])
		{
			vis[e[i].now][now]=1;
			res++;
		}
	return res;
}
void dfs1(int x,int w)
{
	if(x>N/2)
	{
		int now=0;
		for(int i=1;i<=N/2;i++)now=now<<1|v[i];
		insert(now,w);
		return;
	}
	v[x]=0;dfs1(x+1,w);
	v[x]=1;dfs1(x+1,w+a[x]);
	v[x]=1;dfs1(x+1,w-a[x]);
}
void dfs2(int x,int w)
{
	if(x>N)
	{
		int now=0;
		for(int i=N/2+1;i<=N;i++)now=now<<1|v[i];
		ans+=ask(now,w);
		return;
	}
	v[x]=0;dfs2(x+1,w);
	v[x]=1;dfs2(x+1,w+a[x]);
	v[x]=1;dfs2(x+1,w-a[x]);
}
int main()
{
	scanf("%d",&N);
	for(int i=1;i<=N;i++)scanf("%d",&a[i]);
	dfs1(1,0);
	dfs2(N/2+1,0);
	printf("%d",ans-1);
	return 0;
}

---

rp++