CS184.1X 计算机图形学导论（第三讲）

第一单元（介绍关于变换的数学知识）

：基本二维变换

模型坐标系，世界坐标系

1.缩放

Scale(规模，比例)

Sx表示在x方向上放大的倍数，Sy表示在y方向上放大的倍数,因此X坐标乘以Sx，Y坐标乘以Sy

缩放的你操作就是用x坐标和Y坐标分别乘以Sx和Sy的倒数。因此，如果放大了2倍，则其逆操作就是放大1/2倍，就是Sx和Sy的倒数

缩放矩阵是一个对角矩阵，将坐标乘以对应的缩放系数即可。

2.错切

Y坐标不发生变化，因此矩阵的第二行仍然是[0  1]，乘起来仍然是y

x的值等于之前的x的值加上a乘以y坐标的值，x`=x+ay

这里为什么乘以a，因为这里是假设单位长度1，错切的变化量依赖于y坐标的值

错切矩阵为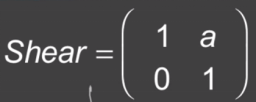，错切的逆矩阵就是把a变成-a，错切公式不变。

3.旋转

该矩阵使得x方向和y方向上的变换叠加，相当于先在x方向上旋转再在y方向上旋转

二维的旋转变换,先在x轴上或先在y轴上可以交换顺序，但是三维不可以

因为数学表示在电脑上书写比较麻烦，故在纸上写下再拍照上传，得出旋转之后坐标的矩阵表示

课后测试题：

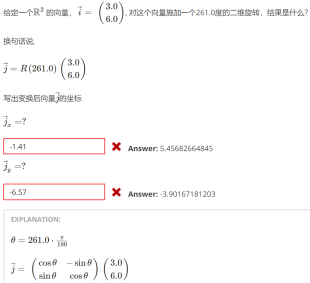
错误原因：在百度的时候没有加度，所以造成了错误，不用像答案把θ进行变换。

：组合变换

矩阵变换顺序不可交换！

组合变换矩阵的逆矩阵：最后一个变换的需要最先逆

对于旋转矩阵来说， R(A+B)=R(A)R(B)，所以R(θ)=R(1)R(2)...R(179)R(180)=R(1+2+...+180)=R(((1+180)*180)/2)=R(16290),需要将旋转角再模360 (因为旋转x 度等价于旋转 x+360度)。 因此, 这里的旋转角就是 16290 mod 360=90 度

：三维旋转

旋转矩阵是正交的，R的转置乘以R等于单位矩阵E

三维绕哪个轴旋转，那个轴的坐标不变，即可得出结论（跟二维推导过程一样）

1>绕Z轴

2>绕X轴

3>绕Y轴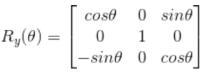（注意这里的形式稍有不同！！）三个矩阵均正交，乘以对应的转置矩阵为单位矩阵

点乘和叉乘的区别：

1.

点乘是一个数，公式：a . b = |a| * |b| * cosθ 
点乘又叫向量的内积、数量积，是一个向量和它在另一个向量上的投影的长度的乘积；
点乘反映着两个向量的“相似度”，两个向量越“相似”，它们的点乘越大。

2.

a*b = |a| * |b| * sinθ ,结果是一个向量，遵循右手法则

旋转可以写成一般矩阵的形式，即某个矩阵M乘以b,下边是一般轴角表示的旋转公式，推导过程比较复杂

罗德里格斯旋转公式：（记住）？？？这里不大懂

反向旋转轴实际上将绕 a⃗ 的逆时针旋转改变为绕a⃗ 的顺时针旋转。因此，绕−a⃗ 的逆时针旋转和绕a⃗ 的顺时针旋转等效。