poj 2104 无修改主席树

题目大意：

求序列的区间第k大

基本思路：

因为我根本就没有思路，知道这是主席树，我就去学了下，在b站上看了uestc的教学视频，然后看了一篇博客，博客http://www.cnblogs.com/Empress/p/4652449.html，我觉得理解的无修改主席树差不多了，也没那么难。下面代码是按照b站上来的，我很喜欢他的离散化方式，不过我不喜欢他的代码风格。

下面阐述我所理解的主席树的基本思路和细节：

转自：http://www.cnblogs.com/Empress/p/4652449.html

这种求区间第k(大)小的题目

最容易想到的做法就是对于每个询问，对[l, r]区间排个序，输出第k小，这样的复杂度是O(m×nlognm×nlogn)

大家都很容易想到排序，但是对于每个询问每个区间排序的代价太大了...

再想想，让我们加入一些线段树的思想，

要求第k小，也就是与个数相关，那么我们可以 以[l,r]区间内的数的个数来建立一棵线段树

结点的值是数的个数，当我们要找第k小的数时，若左子树大于k，那么很显然第k小的数在左子树中；若左子树小于k，那么第k小的数在右子树中

建树的复杂度是O(nlogN)，查询的复杂度是O(logN)      (这里的N是不相同数的数量)

若我们仍对每个查询建树，那么复杂度丝毫没有降低(反而提高了)，那有没有什么办法可以不要每次查询都建树呢？

(让我们联想一下前缀和) 假设我们知道[1, l-1]之间有多少个数比第k小的数小，那么我们只要减去这些数之后在[1, r]区间内第k小的数即是[l, r]区间内的第k小数

更确切的说，我们要求[l, r]区间内的第k小数  可以 用以[1, r]建立的线段树去减去以[1, l-1] 建立的线段树

这样能够减的条件是这两棵树必须是同构的。

若是不太明白， 我们来举个例子：

如有序列  1 2 5 1 3 2 2 5 1 2

我们要求 [5,10]第5小的数

(数列中不存在4、6、7、8 但根据原理就都写出来了，为方便理解，去掉了hash的步骤，实际的代码中其实只要一棵4个叶子节点的树即可)

(红色的为个数)

我们建立的[1, l-1] (也就是[1, 4])之间的树为

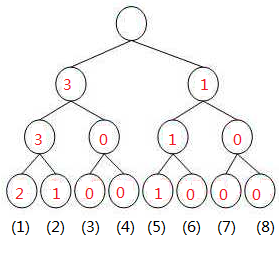
[1, r]也就是[1, 10]的树为

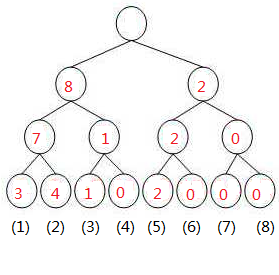
两树相减得到

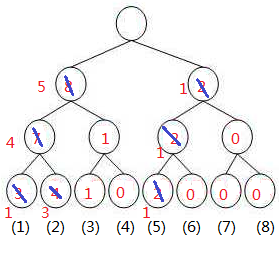
我们来找第5小的数：

发现左子树为5  所以第5小的数在左边， 再往下(左4右1) 发现左边小于5了 ，所以第5小的数在右边 所以第5小的数就是3了

同样的，我们只要建立[1, i] (i是1到n之间的所有值)的所有树，每当询问[l, r]的时候，只要用[1, r]的树减去[1, l-1]的树，再找第k小就好啦

我们将这n个树看成是建立在一个大的线段树里的，也就是这个线段树的每个节点都是一个线段树( ——这就是主席树)

最初所有的树都是空树，我们并不需要建立n个空树，只要建立一个空树，也就是不必每个节点都建立一个空树

插入元素时，我们不去修改任何的结点，而是返回一个新的树( ——这就是函数式线段树)

因为每个节点都不会被修改，所以可以不断的重复用，因此插入操作的复杂度为O(logn)

总的复杂度为O((n+m)lognlogN)   (听说 主席树的芭比说 加上垃圾回收， 可以减少一个log~~~ 然而这只是听说)

你以为这样就结束了吗！！

你没有发现这样空间大到爆炸吗！！！

你在每个节点都建了一个线！段！树！这不MLE才有鬼呢！！！

那怎么办呢？

TiTi表示一棵[1, i]区间的线段树

那么TiTi与Ti−1Ti−1的区别就只有当前插入的这个元素aiai以及它的父亲以及他父亲的父亲以及他父亲的父亲的父亲...

也就是改变的就只有他和他上面logn个数

所以，我们并不需要建一整棵树，我们只需要 单独建立logn个结点，跟Ti−1Ti−1连起来就好了

这样树的空间复杂度(NlogN)

个人认为关键是理解主席树保留了各个历史版本的线段树。

代码如下：

#include<vector>
#include<stack>
#include<algorithm>
#include<cstdio>
#include<cmath>
#include<cstring>
 
using namespace std;
 
typedef long long ll;
const int inf = 0x3f3f3f3f;
const int maxn =100000+10;
int n,m,cnt,root[maxn],a[maxn];
struct node{
    int l,r,sum;
}T[maxn*40];
vector<int>vec;
int getid(int x){
    return lower_bound(vec.begin(),vec.end(),x)-vec.begin()+1;
}
void update(int l,int r,int &x,int y,int pos){
    //之所要用引用，是为了下面改变l，r等
    T[++cnt]=T[y];
    T[cnt].sum++;
    x=cnt;
    if(l==r){
        return;
    }
    int mid=(l+r)/2;
    if(mid>=pos){
        update(l,mid,T[x].l,T[y].l,pos);
    }else{
        update(mid+1,r,T[x].r,T[y].r,pos);
    }
}
int query(int l,int r,int x,int y,int k){
    if(l==r){
        return l;
    }
    int mid=(l+r)/2;
    int sum=T[T[y].l].sum-T[T[x].l].sum;
    //之所以是.l，见上面的例子
    if(sum>=k){
        return query(l,mid,T[x].l,T[y].l,k);
    }else{
        return query(mid+1,r,T[x].r,T[y].r,k-sum);
    }
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        scanf("%d",&a[i]);
        vec.push_back(a[i]);
    }
    sort(vec.begin(),vec.end());
    vec.erase(unique(vec.begin(),vec.end()),vec.end());
    for(int i=1;i<=n;i++){
        update(1,n,root[i],root[i-1],getid(a[i]));
    }
    for(int i=1;i<=m;i++){
        int x,y,k;
        scanf("%d%d%d",&x,&y,&k);
        printf("%d\n",vec[query(1,n,root[x-1],root[y],k)-1]);
        //所以上面是访问了对应的历史版本的线段树
        //因为之前离散化所以现在要还原回来
 
    }
    return 0;
}