HDU-3714 Error Curves(凸函数求极值)

Error Curves

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 6241    Accepted Submission(s): 2341

Problem Description

Josephina is a clever girl and addicted to Machine Learning recently. She
pays much attention to a method called Linear Discriminant Analysis, which
has many interesting properties.
In order to test the algorithm's efficiency, she collects many datasets.
What's more, each data is divided into two parts: training data and test
data. She gets the parameters of the model on training data and test the
model on test data. To her surprise, she finds each dataset's test error curve is just a parabolic curve. A parabolic curve corresponds to a quadratic function. In mathematics, a quadratic function is a polynomial function of the form f(x) = ax2 + bx + c. The quadratic will degrade to linear function if a = 0.

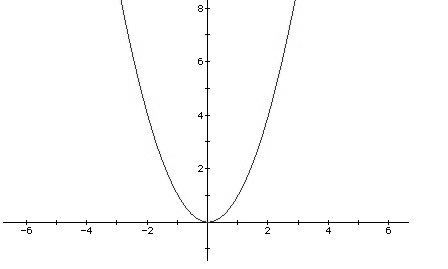
It's very easy to calculate the minimal error if there is only one test error curve. However, there are several datasets, which means Josephina will obtain many parabolic curves. Josephina wants to get the tuned parameters that make the best performance on all datasets. So she should take all error curves into account, i.e., she has to deal with many quadric functions and make a new error definition to represent the total error. Now, she focuses on the following new function's minimum which related to multiple quadric functions. The new function F(x) is defined as follows: F(x) = max(Si(x)), i = 1...n. The domain of x is [0, 1000]. Si(x) is a quadric function. Josephina wonders the minimum of F(x). Unfortunately, it's too hard for her to solve this problem. As a super programmer, can you help her?

 

Input

The input contains multiple test cases. The first line is the number of cases T (T < 100). Each case begins with a number n (n ≤ 10000). Following n lines, each line contains three integers a (0 ≤ a ≤ 100), b (|b| ≤ 5000), c (|c| ≤ 5000), which mean the corresponding coefficients of a quadratic function.

 

Output

For each test case, output the answer in a line. Round to 4 digits after the decimal point.

 

Sample Input

2
1
2 0 0
2
2 0 0
2 -4 2

 

Sample Output

0.0000
0.5000

 

题目的意思就是给出多个开口向上的一元二次方程，求出极大值的最小值，抛物线肯定是凸函数，直接三分就行了

#pragma GCC diagnostic error "-std=c++11"
#include<bits/stdc++.h>
#define _ ios_base::sync_whit_stdio(0);cin.tie(0);
 
using namespace std;
const int N =  + ;
const int INF = (<<);
const double eps = 1e-;
 
double a[N], b[N], c[N];
int n;
 
double fun(double x){
    double res = - INF;
    for(int i = ; i < n; i++)
        res = max(res, a[i] * x * x + b[i] * x + c[i]);
    return res;
}
 
double ternary_search(double L, double R){
    double mid1, mid2;
    while(R - L > eps){
        mid1 = ( * L + R) / ;
        mid2 = (L +  * R) / ;
        if(fun(mid1) >= fun(mid2)) L = mid1;
        else R = mid2;
    }
    return (L + R) * 0.5;
}
 
int main(){
    int T;
    scanf("%d", &T);
    while(T--){
        scanf("%d", &n);
        for(int i = ; i < n; i++){
            scanf("%lf %lf %lf", &a[i], &b[i], &c[i]);
        }
        double x = ternary_search(, );
        printf("%.4f\n", fun(x));
    }
}