POJ1009 Edge Detection

题目来源：http://poj.org/problem?id=1009

题目大意：

　　某图像公司用run length encoding（RLE）的方式记录和存储了大量的图像。程序的目标是读入压缩后的图像，对图像进行边缘检测，然后输出另一幅压缩后的图片。具体形式见下面的图片和描述。

　　一种最简单的边缘检测算法就是使输出图片像素点的值为输入图片中该像素点与其周围像素点值之间差值的最大值。考虑下面的例子：

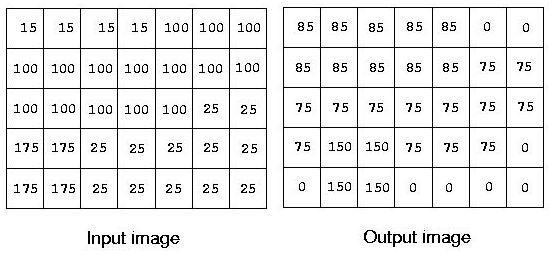
Output image中左上角的像素点的值是|15-15|,|15-100|和|15-100|的最大值85.第4行第2列的像素点值是|175-100|,|175-100|,|175-100|,|175-175|,|175-25|,|175-175|,|175-175|和|175-25|的最小值150.

图像的像素点数在2至1,000,000,000(10⁹)之间。所有的图片以RLE（run length encoding）的方式进行压缩编码。RLE是一些数据对，每对含一个像素值v和一个run length，即有连续多少个点的像素点的值为v。每幅图像最多含有1000个RLE对。连续的数据对的像素值都不相同。图像的每行像素点数相同。

输入：含一张或多张图像，每张图像信息的第一行为图像的宽度，接下来的每行为一个RLE对，以0 0结尾。图像宽度为0时表示图像数据输入完毕。Example Input展示的即为上图所示的图像。

输出：一系列边缘检测后的图像。与输入图像的格式相同，但运行RLE的数目多于1000.

---

Sample Input

7
15 4
100 15
25 2
175 2
25 5
175 2
25 5
0 0
10
35 500000000
200 500000000
0 0
3
255 1
10 1
255 2
10 1
255 2
10 1
255 1
0 0
0

Sample Output

7
85 5
0 2
85 5
75 10
150 2
75 3
0 2
150 2
0 4
0 0
10
0 499999990
165 20
0 499999990
0 0
3
245 9
0 0
0

---

刚开始直接用暴力方法做，发现数据量大时计算时间过长，TLE了。后来看了牛人的方法表示无比佩服。

　　对于本题有如下观察：

　　1.由于图片的像素点数最大为10^9，而RLE对的数目最大为1000，所以，一定存在一些RLE的run length很长，使得图像中有比较多的连续像素值相等，也即对他们的很多点进行边缘检测后的值一定为0，所以不必再逐个计算。

　　2.实际上我们只需要关注结果值会与其前面的点不一样的点即可（取名为关键点），由这些关键点即可得到输出图像的RLE对。

　　对于第2点，哪些点会是关键点呢？大牛分析后发现，每个输入的RLE对的起点和终点以及这些点周围的点一定包含了所有的关键点。如何证明？我没有去想怎么从理论上严格的推倒，只是从直觉上，我觉得可以这样来想象这个问题：

　　首先把整幅图想象成一张白纸（比如把全部像素点的值初始化为0）。每读入一个RLE对，就相当于用彩笔在纸上给指定数目的像素点涂上了颜色。而每多涂一次颜色，该次涂色的起点和终点处及其周边的点的输出值会受到影响，有可能会变得跟其前一个点的输出值不一样（这个在纸上试一试就能发现），也就是说有可能成为关键点。而其他点的输出值应该是跟其左边的点输出值相等。所以当处理完了每个RLE对，也就把所有可能成为关键点的点的输出值都计算出来了。然后按坐标将所有点排序，再把输出值相等的点合并起来，就可以得到输出的RLE对。

　　具体实现可以下列参考代码，但是效率可能不是很高，应该还可以继续优化。

 //////////////////////////////////////////////////////////////////////////
 //        POJ1009 Edgee Detection
 //        Memory: 656K        Time: 172MS
 //        Language: C++        Result: Accepted
 //////////////////////////////////////////////////////////////////////////

 #include <iostream>
 #include <map>
 #include <math.h>
 #include <stdlib.h>

 #define getBigger(a, b) ((a > b) ? a : b)
 #define upLeft(i)  (i - c - 1)
 #define up(i)  (i - c)
 #define upRight(i)  (i - c + 1)
 #define left(i)  (i - 1)
 #define right(i)  (i + 1)
 #define downLeft(i)  (i + c - 1)
 #define down(i)  (i + c)
 #define downRight(i)  (i + c + 1)

 using namespace std;

 class RLE {
 public:
     int color;
     int length;
     int startPoint;
     int endPoint;
 };

 RLE RLEList[];
 int n;//RLE表长度
 int pointCount; //总点数
 int c, r;//image的列数与行数
 map<int, int> PVmap;

 int getColor(int index) {
     for(int i = ; i < n; i++) {
         if (index <= RLEList[i].endPoint) {
             return RLEList[i].color;
         } else {
             continue;
         }
     }
 } 

 int getValue(int i) {
     int value = ;

     if ((upLeft(i) >= ) && ((i % c) > )) {
         value = getBigger(value, abs(getColor(i) - getColor(upLeft(i))));
     }
     if ((up(i) >=  )) {
         value = getBigger(value, abs(getColor(i) - getColor(up(i))));
     }
     if ((upRight(i) >= ) && ((i % c) < c - )) {
         value = getBigger(value, abs(getColor(i) - getColor(upRight(i))));
     }
     if ((left(i) >= ) && ((i % c) > )) {
         value = getBigger(value, abs(getColor(i) - getColor(left(i))));
     }
     if ((right(i) <= r * c - ) && ((i % c) < c - )) {
         value = getBigger(value, abs(getColor(i) - getColor(right(i))));
     }
     if ((downLeft(i) <= r * c - ) && ((i % c) > )) {
         value = getBigger(value, abs(getColor(i) - getColor(downLeft(i))));
     }
     if ((down(i) <= r * c - )) {
         value = getBigger(value, abs(getColor(i) - getColor(down(i))));
     }
     if ((downRight(i) <= r * c - ) && ((i % c) < c - )) {
         value = getBigger(value, abs(getColor(i) - getColor(downRight(i))));
     }
     return value;
 }

 void processPos(int index) {
     if (PVmap.find(index) == PVmap.end()) {
         PVmap[index] = getValue(index);
     }
     if (upLeft(index) >= && upLeft(index) < pointCount) {
         if (PVmap.find(upLeft(index)) == PVmap.end()) {
             PVmap[upLeft(index)] = getValue(upLeft(index));
         }
     }
     if (up(index) >= && up(index) < pointCount) {
         if (PVmap.find(up(index)) == PVmap.end()) {
             PVmap[up(index)] = getValue(up(index));
         }
     }
     if (upRight(index) >= && upRight(index) < pointCount) {
         if (PVmap.find(upRight(index)) == PVmap.end()) {
             PVmap[upRight(index)] = getValue(upRight(index));
         }
     }
     if (left(index) >= && left(index) < pointCount) {
         if (PVmap.find(left(index)) == PVmap.end()) {
             PVmap[left(index)] = getValue(left(index));
         }
     }
     if (right(index) >= && right(index) < pointCount) {
         if (PVmap.find(right(index)) == PVmap.end()) {
             PVmap[right(index)] = getValue(right(index));
         }
     }
     if (downLeft(index) >= && downLeft(index) < pointCount) {
         if (PVmap.find(downLeft(index)) == PVmap.end()) {
             PVmap[downLeft(index)] = getValue(downLeft(index));
         }
     }
     if (down(index) >= && down(index) < pointCount) {
         if (PVmap.find(down(index)) == PVmap.end()) {
             PVmap[down(index)] = getValue(down(index));
         }
     }
     if (downRight(index) >= && downRight(index) < pointCount) {
         if (PVmap.find(downRight(index)) == PVmap.end()) {
             PVmap[downRight(index)] = getValue(downRight(index));
         }
     }
 }

 int main(void) {
     c = ;
     while (true) {
         cin >> c;
         if (c == ) {
             cout << "" << endl;
             return ;
         }
         pointCount = ;
         int i = ;
         while (true) {
             int color, length;
             cin >> color >> length;
             if (length == ) {
                 break;
             }
             RLEList[i].color = color;
             RLEList[i].length = length;
             i++;
             pointCount += length;
         }
         r = pointCount / c;
         if (pointCount % c) {
             r++;
             RLEList[i].length = r * c - pointCount;
             RLEList[i].color = ;
             pointCount = r * c;
             i++;
         }
         n = i;
         RLEList[].startPoint = ;
         RLEList[].endPoint = RLEList[].length - ;
         for (int i = ; i < n; i++) {
             RLEList[i].startPoint = RLEList[i - ].startPoint + RLEList[i - ].length;
             RLEList[i].endPoint = RLEList[i - ].endPoint + RLEList[i].length;
         }
         cout << c << endl;
         //处理每个RLE对的起点和终点产生的影响
         for (int RLEIndex = ; RLEIndex < n; RLEIndex++) {
             int startPos = RLEList[RLEIndex].startPoint;
             int endPos = RLEList[RLEIndex].endPoint;
             processPos(startPos);
             processPos(endPos);
         }
         map<int, int>::iterator it1;
         map<int, int>::iterator it2;
         int l = ;
         //合并output image中相同的关键点，输出RLE对
         for (it1 = PVmap.begin(), it2 = it1, ++it2; it2 != PVmap.end(); ++it1, ++it2) {
             if((*it2).second == (*it1).second) {
                 l += (*it2).first - (*it1).first;
             } else {
                 cout << (*it1).second << " " << l << endl;
                 l = ;
             }
         }
         --it2;
         cout << (*it2).second << " " << l << endl;
         cout << "0 0"<< endl;
         PVmap.clear();
     }
     return ;
 }