最小生成数kruskal算法和prim算法

定义

连通图：在无向图中，若任意两个顶点vivi与vjvj都有路径相通，则称该无向图为连通图。

强连通图：在有向图中，若任意两个顶点vivi与vjvj都有路径相通，则称该有向图为强连通图。

连通网：在连通图中，若图的边具有一定的意义，每一条边都对应着一个数，称为权；权代表着连接连个顶点的代价，称这种连通图叫做连通网。

生成树：一个连通图的生成树是指一个连通子图，它含有图中全部n个顶点，但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边，如果生成树中再添加一条边，则必定成环。

最小生成树：在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树。

kruskal算法

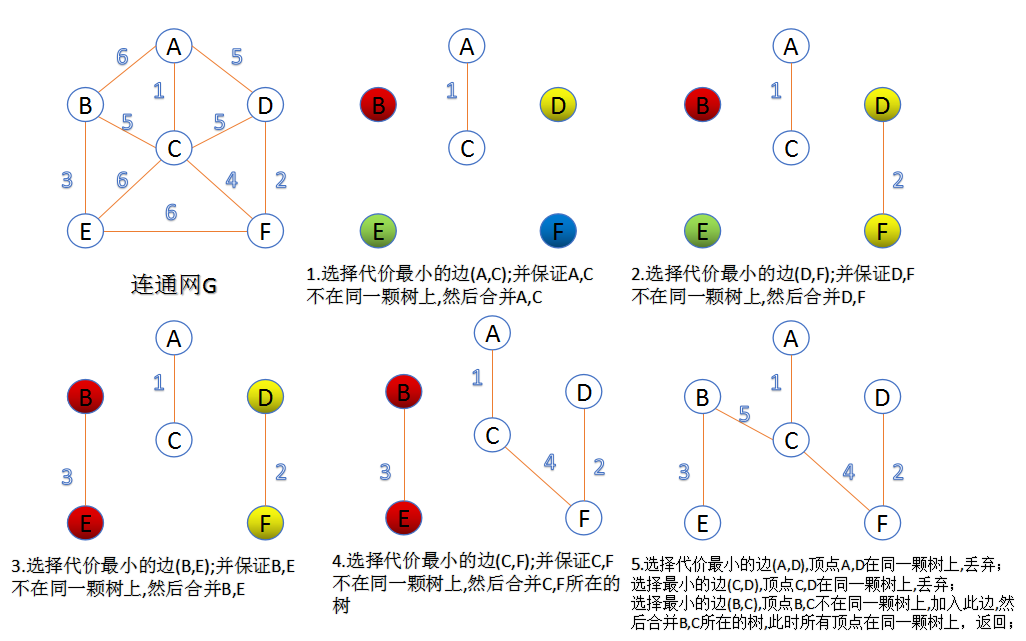
此算法可以称为“加边法”，初始最小生成树边数为0，每迭代一次就选择一条满足条件的最小代价边，加入到最小生成树的边集合里。

1. 把图中的所有边按代价从小到大排序；

2. 把图中的n个顶点看成独立的n棵树组成的森林；

3. 按权值从小到大选择边，所选的边连接的两个顶点ui,viui,vi,应属于两颗不同的树，则成为最小生成树的一条边，并将这两颗树合并作为一颗树。

4. 重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。

prim算法

此算法可以称为“加点法”，每次迭代选择代价最小的边对应的点，加入到最小生成树中。算法从某一个顶点s开始，逐渐长大覆盖整个连通网的所有顶点。

1. 图的所有顶点集合为VV；初始令集合u={s},v=V−uu={s},v=V−u;

2. 在两个集合u,vu,v能够组成的边中，选择一条代价最小的边(u0,v0)(u0,v0)，加入到最小生成树中，并把v0v0并入到集合u中。

3. 重复上述步骤，直到最小生成树有n-1条边或者n个顶点为止。

kruskal算法：

#include <iostream>
#include <list>
#include <vector>
#include <algorithm>

const int   INFINITE  = 0x7FFFFFFF;
const int   VERTEX    = ;
const char  szVertex[] = { 'A', 'B', 'C', 'D', 'E', 'F' };

struct stEdge
{
    int u;
    int v;
    int weight;

    stEdge(int iu, int iv, int iweight):u(iu),v(iv),weight(iweight) {}

    friend bool operator<(const stEdge &a, const stEdge &b) { return a.weight < b.weight; }
};

void createGraph(int (*g)[VERTEX])
{
    for (int i = ; i < VERTEX; i++)
    {
        for (int j = ; j < VERTEX; j++)
        {
            g[i][j] = INFINITE;
        }
    }
    g[][] = ; g[][] = ; g[][] = ;
    g[][] = ; g[][] = ; g[][] = ;
    g[][] = ; g[][] = ; g[][] = ; g[][] = ; g[][] = ;
    g[][] = ; g[][] = ; g[][] = ;
    g[][] = ; g[][] = ; g[][] = ;
    g[][] = ; g[][] = ; g[][] = ;
}

void initEdges(std::vector<stEdge> &edges, const int (*g)[VERTEX])
{
    for (int i = ; i < VERTEX; ++i)
    {
        for (int j = i+; j < VERTEX; ++j)
        {
            edges.push_back(stEdge(i,j,g[i][j]));
        }
    }
    std::sort(edges.begin(), edges.end(), std::less<stEdge>());
}

bool notSameTree(int u, int v, std::vector<std::list<int> > &trees)
{
    int uindex = -, vindex = -;

    for (int i = ; i < VERTEX; ++i)
    {
        if (std::find(trees[i].begin(), trees[i].end(), u) != trees[i].end())
        {
            uindex = i;
        }
        if (std::find(trees[i].begin(), trees[i].end(), v) != trees[i].end())
        {
            vindex = i;
        }
    }

    if (uindex != vindex)
    {
        trees[uindex].splice(trees[uindex].end(), trees[vindex]);
        return true;
    }

    return false;
}

void kruskal(const int (*g)[VERTEX])
{
    std::vector<stEdge> edges;
    initEdges(edges, g);

    std::vector<std::list<int> > trees(VERTEX);
    for (int i = ; i < VERTEX; ++i)
    {
        trees[i].push_back(i);
    }

    for (auto e : edges)
    {
        if (notSameTree(e.u, e.v, trees))
        {
            std::cout << szVertex[e.u] << "---" << szVertex[e.v] << std::endl;
        }
    }
}

int main()
{
    int g[VERTEX][VERTEX] = {};

    createGraph(g);

    kruskal(g);

    return ;
}

prim算法：

#include <iostream>
#include <list>
#include <vector>
#include <algorithm>

const int   INFINITE  = 0x7FFFFFFF;
const int   VERTEX    = ;
const char  szVertex[] = { 'A', 'B', 'C', 'D', 'E', 'F' };

struct stEdge
{
    int index;
    int weight;
};

void createGraph(int (*g)[VERTEX])
{
    for (int i = ; i < VERTEX; i++)
    {
        for (int j = ; j < VERTEX; j++)
        {
            g[i][j] = INFINITE;
        }
    }
    g[][] = ; g[][] = ; g[][] = ;
    g[][] = ; g[][] = ; g[][] = ;
    g[][] = ; g[][] = ; g[][] = ; g[][] = ; g[][] = ;
    g[][] = ; g[][] = ; g[][] = ;
    g[][] = ; g[][] = ; g[][] = ;
    g[][] = ; g[][] = ; g[][] = ;
}

int minIndex(const stEdge *weightArr, int len)
{
    int min = INFINITE;
    int idx = -;

    for (int i = ; i < len; ++i)
    {
        if (weightArr[i].weight !=  && min > weightArr[i].weight)
        {
            min = weightArr[i].weight;
            idx = i;
        }
    }

    return idx;
}

void prim(const int (*g)[VERTEX], int index)
{
    stEdge weightArr[VERTEX];

    weightArr[index].weight = ;
    weightArr[index].index = index;
    for (int i = ; i < VERTEX; ++i)
    {
        if (i != index)
        {
            weightArr[i].index = index;
            weightArr[i].weight = g[index][i];
        }
    }

    for (int i = ; i < VERTEX; ++i)
    {
        int nextIndex = minIndex(weightArr, VERTEX);
        if (nextIndex != -)
        {
            std::cout << szVertex[weightArr[nextIndex].index] << "---" << szVertex[nextIndex] << std::endl;

            weightArr[nextIndex].weight = ;
            weightArr[nextIndex].index = nextIndex;
            for (int j = ; j < VERTEX; ++j)
            {
                if (weightArr[j].weight !=  && g[nextIndex][j] < weightArr[j].weight)
                {
                    weightArr[j].index = nextIndex;
                    weightArr[j].weight = g[nextIndex][j];
                }
            }
        }
    }
}

int main()
{
    int g[VERTEX][VERTEX] = {};

    createGraph(g);

    prim(g, );

    return ;
}

转载自：https://blog.csdn.net/luoshixian099/article/details/51908175