机器学习：PCA（基础理解、降维理解）

PCA（Principal Component Analysis）

一、指导思想

• 降维是实现数据优化的手段，主成分分析（PCA）是实现降维的手段；

• 降维是在训练算法模型前对数据集进行处理，会丢失信息。

• 降维后，如果丢失了过多的信息，在我们不能容忍的范围里，就不应该降维。

• 降维没有正确与否的标准，只有丢失信息的多少；

• 降维的方式本质是有无穷多种的。我们期望在其中找到“最好”，或者说“丢失信息”最少的那一种；

• PCA算法使用的是：降维后保持原始数据的方差的多少，来衡量降维后保持原始数据了多少信息；

• 对于降维算法来说，这个衡量标准不是固定的，有其他降维方法使用其他的衡量标准。

• 降维不等于降噪，降噪只是降维可能的结果，但不是一定的结果，尤其是原始信息完全没有噪音的时候。

• 每个主成分都解释了原始数据方差的一部分。每个主成分解释的方差量越大，说明这个主成分越重要。

1. 可以这样理解：一个数据的主成分反应了一个新的降维后的特征空间，数据被降维后得到新的数据集，新的数据集在降维后的空间内的分布，只反应了原始数据在原始特征空间中的分布的一部分情况；

• 信息损失依然可以表达原有信息是很常见的事情。如果举一个抽象的例子，我们日常在互联网中用的图像压缩算法，比如jpg等，都是通过减少图像原有信息达到让图片文件更小的目的。利用的就是即使损失了信息，对原有图像主体信息的影响是不大的。但是压缩的太狠了，就会慢慢让整个图像越来越模糊，最终导致完全看不出是什么东西，这就是信息损失的太大了。

• PCA不是进行特征选择的过程。PCA的降维过程，是将原始的高维空间，映射到一个低维空间。低维空间的每个维度，是原始高维空间的一个线性组合。这使得PCA后的低维空间，每一个维度丧失了语意。如果对于你的应用来说，保持特征语意很重要，又要减少特征量，是不建议使用PCA的：）

• 思路：

1. 降维的目的：优化数据集；
2. 得到优化的数据集的前提：找到最佳的降维空间；
3. 满足最佳的降维空间的条件：降维后的数据集的方差最大；
4. 使方差最大的优化方法：梯度上升法；

• 其它

1. 不能拿现实中的物理空间，类比数据中的特征空间；
2. n 维向量（或者 n 维数组）只在数学中表示，n 维空间只是形象的表示数据间的关联；
3. 在物理空间中，四维空间（时空，空间 + 时间维度）已经是极限了；

• 疑问

1. 怎么判断要不要降维？
2. 或者说怎么判断数据集适不适合降维？
3. 或者说这些数据集怎么了，要降低它的维度？
4. 怎么判断降维后有没有丢失关键数据？是通过降维后的数据训练处的模型的效果吗？
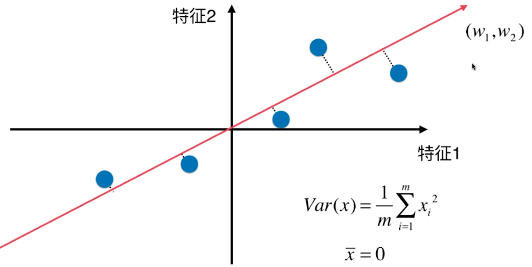
5. 降维过程中，降维后的数据集的方差的求解公式中：向量 w 表示什么？
6. 降维实例中，二维特征空间降成一维（一条直线），w 是该直线上的一个单位向量，感觉是方便计算方差而引入的，为什么可以直接推广到 n 维特征空间的降维中使用？

• 答疑

1. 问题1、2、3：
2. 问题5：向量 w 就是数据集的一个主成分；

二、对 PCA 的理解

• 名称：主成分分析算法；

• 类型：非监督机器学习算法；

• 主要功能：主要用于数据的降维；

• 其它应用：数据可视化、去燥；

• 不仅在机器学习领域应用，也是统计学领域的重要应用

• 数据降维的意义

1. 从数据中发现更便于人类理解的特征；
2. 方便数据可视化，使人类更容易理解可视化后的数据；
3. 提高算法的运行效率；
4. 有时，数据经过主成分分析以后再用于机器学习算法，数据的被识别率更好；

三、降维

　1）实例说明数据的降维

• 二维特征空间的样本点
• 

• 方案（一）：抛除特征一，降维后的特征关系
• 

• 方案（二）：抛除特征二，降维后的数据关系
• 

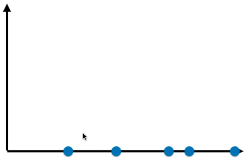
• 两种降维方案，方案（二）更好：

1. 方案（二）降维后的样本点映射到坐标轴上，点与点之间的距离较大，说明样本点之间具有较高的可区分度；
2. 更好的保持了原来的点与点（二维特征空间里的样本点）之间的距离；

　2）PCA 方法降维

• 疑问：有没有更好的降维方案？

• 什么叫更好：使样本的区分度更加明显

• 方案（三）
• 

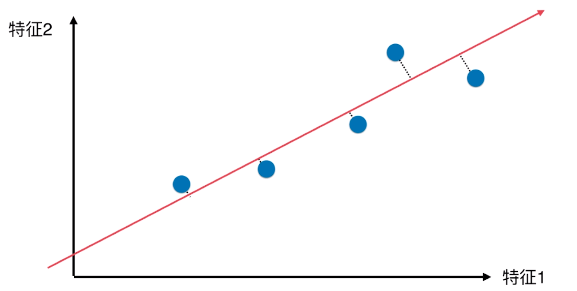
• 降维后的样本点分布
• 

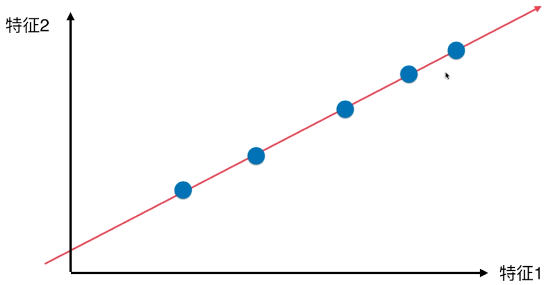
• 优点：

1. 所有的样本点的差异（或者距离），更趋近原来二维特征空间内样本点的差异（或距离）；
2. 与方案（一）、方案（二）相比，样本的区分度更加明显；

　3）降维后的特征空间

• 最佳的降维特征空间满足的条件：映射到降维特征空间后的数据集的方差最大时，对应的降维空间最佳；

　　1、分析

• 问题（一）：怎么找到这样的一条直线？（让降维后的样本间间距最大）
• 在二维特征空间中，这条直线就是降维后的特征空间；

• 问题（二）：如何定义样本间间距？
• 方案：使用方差（Variance）表示样本间的距离；

• 方差：描述样本（数据）在空间内（可以是一维、二维、多维空间）分布疏密的指标，方差越大，样本之间越稀疏；方差越小，样本之间越紧密；

1. 方差公式： ；
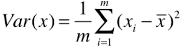2. x_i：m 个数据中的第 i 个数据；

　　2、二维特征空间降维成一维特征空间

• 思路：找到一个轴，得到样本空间的所有点映射到这个轴后，方差最大（表示样本间间距越大）；

• 具体操作步骤：

　　　A、第一步：将每一种特征的均值归为 0 （此过程称为 demean）

　　　　# 样本分布没变，移动坐标轴位置，得到样本在每一个维度的均值都为 0 ；（见下图）

　　　　# 具体操作：将数据集的每一种特征的值减去本列特征的均值；

　　　　# 公式变形：，均值；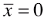

            # X_i ：值映射到新的坐标轴上之后，得到的新的样本；

　　　B、第二步：求一个轴的方向 w = (w₁ , w₂)，使得所有的样本映射到 w 以后，有：

　　　　　　　　# 轴：新的特征空间；

　　　　　　　　# w：新的特征空间的第一主成分；

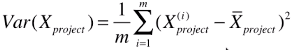最大；

　　　   # 公式变形后：

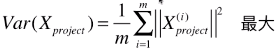
1. Var(X_project)：映射后的样本的方差；
2. X_preject：映射后的数据集；
3. || X_preject⁽ⁱ⁾ ||：映射后的数据集的第 i 个样本向量的模；（映射时，在原始特征空间内，将样本点看做向量）

• 

　　# 注：此直线，不是线性回归的线性模型直线，本例只是简化为对二维空间内的只有两个特征的样本数据进行降维；

　　# 线性回归中，直线模型是样本的 n 维特征和样本对应的输出值之间的关系

　4）映射过程

• 映射过程就是一个向量投影到另一个向量上

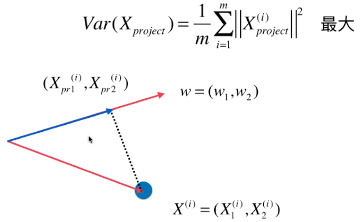
1. w = (w₁, w₂)：新的特征空间的主成分（此例中指，特征空间中，目标轴的方向）；
2. X⁽ⁱ⁾：特征空间中，数据集的第 i 个样本；
3. X⁽ⁱ⁾ =  ( X₁⁽ⁱ⁾,  X_2⁽ⁱ⁾ )：特征空间中，样本点也可以看做一个向量；
4. (X_pr1⁽ⁱ⁾,  X_pr2⁽ⁱ⁾)：映射后的样本点的特征值；

• 计算映射后的样本特征

　　　# 其实就是向量之间的运算；

　　

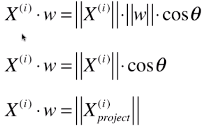
1. θ：两向量的夹角；

• 公式变形：；

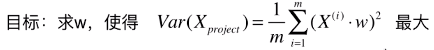1. 此公式是针对本例中的两个特征的样本；
2. 称此向量 w 是数据集的一个主成分；

四、n 维特征空间降维

　1）公式推广

• 推广到 n 为空间（一个样本有 n 个特征）：
• 变形公式：

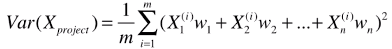
1. X⁽ⁱ⁾.dot(w)：括号内的相加的式子，就是样本与主成分的向量积；

• 再次变形，得最终公式：

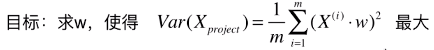
1. X⁽ⁱ⁾：第 i 个样本；
2. w：主成分；

　2）分析

1. 降维的目的：优化数据集；
2. 降维的手段：主成分分析法（PCA）；
3. 优化结果：得到新的数据集  X_preject ；
4. PCA的手段：优化目标函数，使得其最大时对应的；

五、其它降维算法

• MDS，Isomap，LLE，LDA，t-SNE