24最小生成树之Prim算法

最小生成树的Prim算法

思想：采用子树延伸法

将顶点分成两类：

生长点——已经在生成树上的顶点

非生长点——未长到生成树上的顶点

使用待选边表：

每个非生长点在待选边表中有一条待选边，一端连着非生长点，另一端连着生长点

步骤：

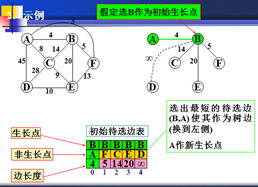
步骤1）构造初始待选边表，任选一个顶点v作为初始生长点，对其余每个非生长点w（共n-1个），将边（w，v）加进待选边表，如果边（w，v）不存在，则认为边（w，v）的长度是∞。

步骤2）循环n-2遍，非生长点个数k从n-1变到1。

①选择树边。

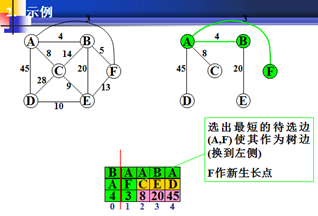
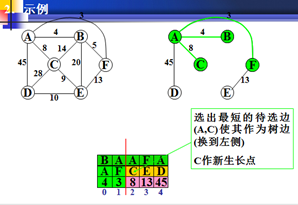
从待选边表中选出一条最短的待选边（u，v），这里u是非生长点，v是生长点，将（u，v）从待选边表移入生成树的边集，并且将u作为新选出的生长点。

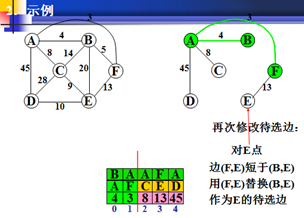
②修改待选边

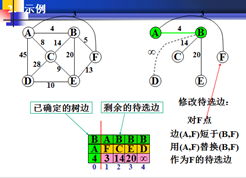
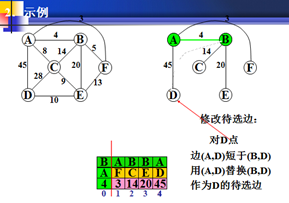
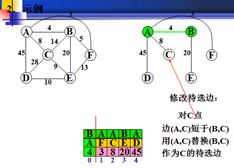
对剩下的每个非生长点w，比较待选边是（w，x）与边（w，u）的长度，这里x是原有的生长点，u是新选出的生长点，如果（w，u）短于边（w，x），则用（w，u）代替（w，x），作为w的待选边；否则，什么也不做。

示例:

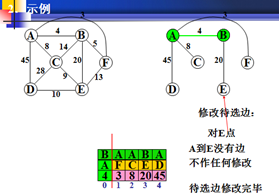
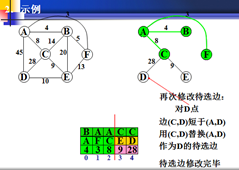
以上为官方图例，如果看不懂可以看下面的世俗图解。。。。。。。。。。。。。。。。

B为生长点,列出所有与B连接点权值。

B	B	B	B	B
C	A	D	E	F
14	4	∞	20	5

1.再以权值最小的为生长点，发现B-A的权值最小。A为新的生长点。

及B-A的边确定了。

2.A的为生长点与B原来的边进行比较，若小于原来，就交换。

A-C  8 小于  B-C  交换

A-D  45 小于 B-D  交换

A-E  ∞  大于 B-E  不交换

A-F  3  小于  B-F  交换

B	A	A	B	A
A	C	D	E	F
4	8	45	20	3

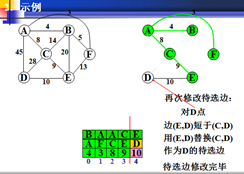
在以权值最小为生长点。F为新的生长点。

同理，F分别于A原来的权值，进行比较（如上步骤）

B	A	A	A	F
A	F	C	D	E
4	3	8	45	13

在以权值最小为生长点。C为新的生长点。

B	A	A	C	C
A	F	C	D	E
4	3	8	28	9

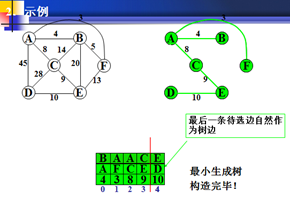
在以权值最小为生长点。E为新的生长点。

B	A	A	C	E
A	F	C	E	D
4	3	8	9	10

结束。按结点和权值依次画出最小生成树。

注意点：

1.要找准新的生长点（权值最小那个）。

2.找准新生长点后，要以新的生长点与各节点的权值，和原来生长点与各节点点权值，进行足一比较，小于原来的就交换。否则，保持原来的结点和权值。

实现方法分析：

（1）图的边集存储形式

采用邻接数组存储，便于比较边长度，只需存储邻接矩阵的下三角部分（无向加权图）。

（2）待选边表和树边集的存储形式

如上例，待选边表和树边集共用一个长度为n-1的数组存储，元素含3个域：生长点和非生长点名称，边长度。

（3）处理步骤（循环n-2遍）

如上例，每次从当前待选边中选出最短边作树边，换到数组左段的右端，修改剩下的待选边。

Prim算法与Kruskal算法对照:

1）主要思想——都是选短边，但选法不同

Kruskal算法从全图中选短边。

Prim算法从待选边表中选短边。

2）直观性

Kruskal采用子树合并法（直观）

Prim算采用子树延伸法

3）实现的难易程度

Kruskal算法需要判断回路（实现困难些）

Prim算法不需要判断回路

4）时间复杂性

Kruskal算法执行时间主要花费在判断回路，所需时间不超过O(mlogm)，m是边数

Prim算法执行时间主要花费在n-2次修改待选边表，其时间耗费用量是O(n2)阶的，n是顶点数

Kruskal算法适用于顶点数较多，而边数较少的情况

Prim算法适用于顶点数较少，而边数较多的情况