经典算法 Morris遍历

内容：

1、什么是morris遍历

2、morris遍历规则与过程

3、先序及中序

4、后序

5、morris遍历时间复杂度分析

1、什么是morris遍历

关于二叉树先序、中序、后序遍历的递归和非递归版本，在这里有详细代码：https://www.cnblogs.com/wyb666/p/10176980.html

明显这6种遍历算法的时间复杂度都需要 O(H) （H 为树高）的额外空间复杂度

另外因为二叉树遍历过程中只能向下查找孩子节点而无法回溯父结点，因此这些算法借助栈来保存要回溯的父节点

并且栈要保证至少能容纳下 H 个元素（比如遍历到叶子结点时回溯父节点，要保证其所有父节点在栈中）

而morris遍历则能做到时间复杂度仍为 O(N) 的情况下额外空间复杂度只需 O(1) 。

2、morris遍历规则与过程

首先在介绍morris遍历之前，我们先把先序、中序、后序定义的规则抛之脑后，

比如先序遍历在拿到一棵树之后先 遍历头结点然后是左子树后是右子树，并且在遍历过程中对于子树的遍历仍是这样。

在忘掉这些遍历规则之后，我们来看一下morris遍历定义的标准：

(1)定义一个遍历指针 cur ，该指针首先指向头结点

(2)判断 cur 的左子树是否存在

　　如果 cur 的左孩子为空，说明 cur 的左子树不存在，那么 cur右移(cur=cur.right)

　　如果 cur 的左孩子为cur，说明 cur 的左子树存在，找出该左子树上最右节点记为 mostRight

　　　　如果mostRight 的右孩子为空，那就让其指向 cur （ mostRight.right=cur ），并左移 cur （ cur=cur.left ）

　　　　如果mostRight 的右孩子不为空，那么让 cur 右移（ cur=cur.right ），并将 mostRight 的右孩子置空

(3)经过步骤2之后，如果 cur 不为空，那么继续对 cur 进行步骤2，否则遍历结束

下图所示举例演示morris遍历的整个过程：

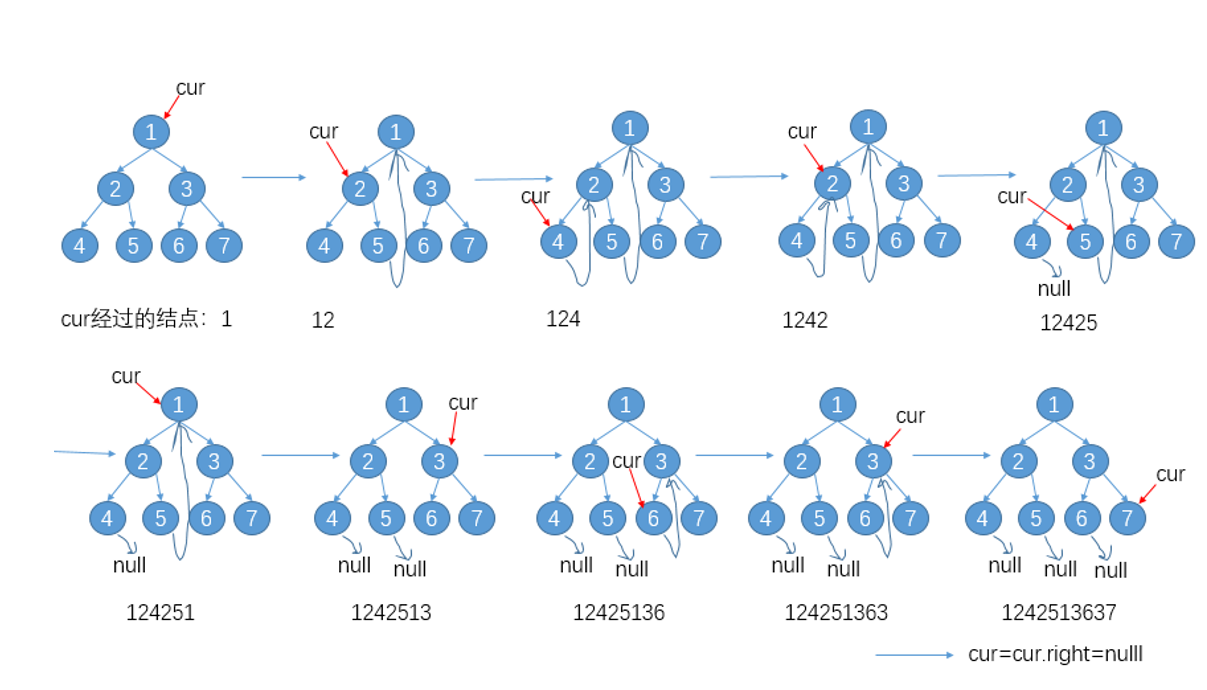
代码1：

 public static void morrisProcess(Node head){
     // morris遍历的过程 第一种写法
     if(head == null){
         return;
     }
     Node cur = head;
     Node mostRight = null;
     while(cur!=null){
         mostRight = cur.left;
         if(mostRight != null){
             while(mostRight.right!= null && mostRight.right!=cur){
                 mostRight = mostRight.right;
             }
             if(mostRight.right==null){
                 mostRight.right = cur;
                 cur = cur.left;
                 continue;
             } else{
                 mostRight.right = null;
             }
         }
         cur = cur.right;
     }
 }

代码2：

 public static void morrisProcess2(Node head) {
     // morris遍历的过程  第二种写法
     if (head == null) {
         return;
     }
     Node cur = head;
     Node mostRight = null;
     while (cur != null) {
         mostRight = cur.left;
         if (mostRight == null) {
             cur = cur.right;
         } else {
             while (mostRight.right != null && mostRight.right != cur) {
                 mostRight = mostRight.right;
             }
             if (mostRight.right == null) {
                 mostRight.right = cur;
                 cur = cur.left;
             } else {
                 mostRight.right = null;
                 cur = cur.right;
             }
         }
     }
 }

3、先序及中序

遍历完成后对 cur 进过的节点序列稍作处理就很容易得到该二叉树的先序、中序序列：

morris遍历会来到一个左孩子不为空的结点两次，而其它结点只会经过一次

因此使用 morris遍历打印先序序列时:

• 如果来到的结点无左孩子，那么直接打印（只会经过一次）
• 如果来到的结点的左子树的右结点的右孩子为空才打印（第一次来到该结点时）

而使用morris遍历打印中序序列时:

• 如果来到的结点无左孩子，那么直接打印 （只会经过一次）
• 如果来到的结点的左子树的右结点不为空时才打印（第二次来到该结点时）
• 上述两种情况实际上可以总结成一种情况：在cur右移时打印

遍历代码如下：

 public static void morrisPre(Node head) {
     // morris先序遍历 =》第一次来到节点就打印
     if (head == null) {
         return;
     }
     Node cur = head;
     while (cur != null) {
         if (cur.left == null) {
             System.out.print(cur.value + " ");
             cur = cur.right;
         } else {
             Node mostRight = cur.left;
             while (mostRight.right != null && mostRight.right != cur) {
                 mostRight = mostRight.right;
             }
             if (mostRight.right == null) {
                 System.out.print(cur.value + " ");
                 mostRight.right = cur;
                 cur = cur.left;
             } else {
                 mostRight.right = null;
                 cur = cur.right;
             }
         }
     }
     System.out.println();
 }

 public static void morrisIn(Node head) {
     // morris中序遍历 =》放在cur右移的位置打印
     if (head == null) {
         return;
     }
     Node cur = head;
     while (cur != null) {
         if (cur.left == null) {
             System.out.print(cur.value + " ");
             cur = cur.right;
         } else {
             Node mostRight = cur.left;
             while (mostRight.right != null && mostRight.right != cur) {
                 mostRight = mostRight.right;
             }
             if (mostRight.right == null) {
                 mostRight.right = cur;
                 cur = cur.left;
             } else {
                 System.out.print(cur.value + " ");
                 mostRight.right = null;
                 cur = cur.right;
             }
         }
     }
     System.out.println();
 }

4、后序

使用morris遍历得到二叉树的后序序列就没那么容易了，因为对于树种的非叶结点，

morris遍历都会经过它两 次，而我们后序遍历实在是在第三次来到该结点时打印该结点的。

因此要想得到后序序列，仅仅改变在morris遍历时打印结点的时机是无法做到的。

morris实现后序遍历：如果在每次遇到第二次经过的结点时，将该结点的左子树的右边界上的结点

从下到上打印，最后再将整颗树的右边界从下到上打印，终就是这个数的后序序列：

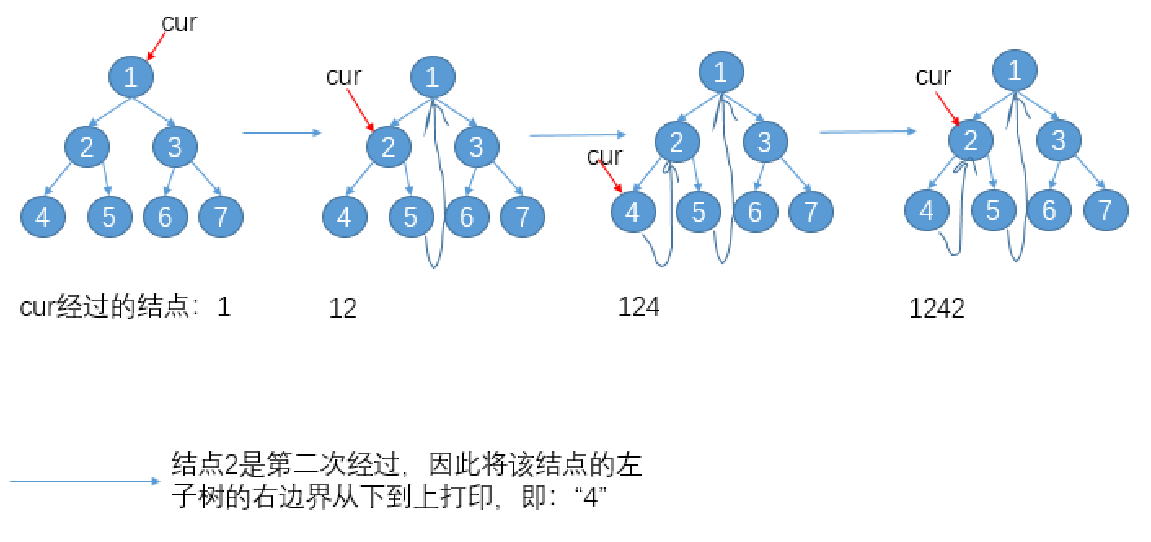
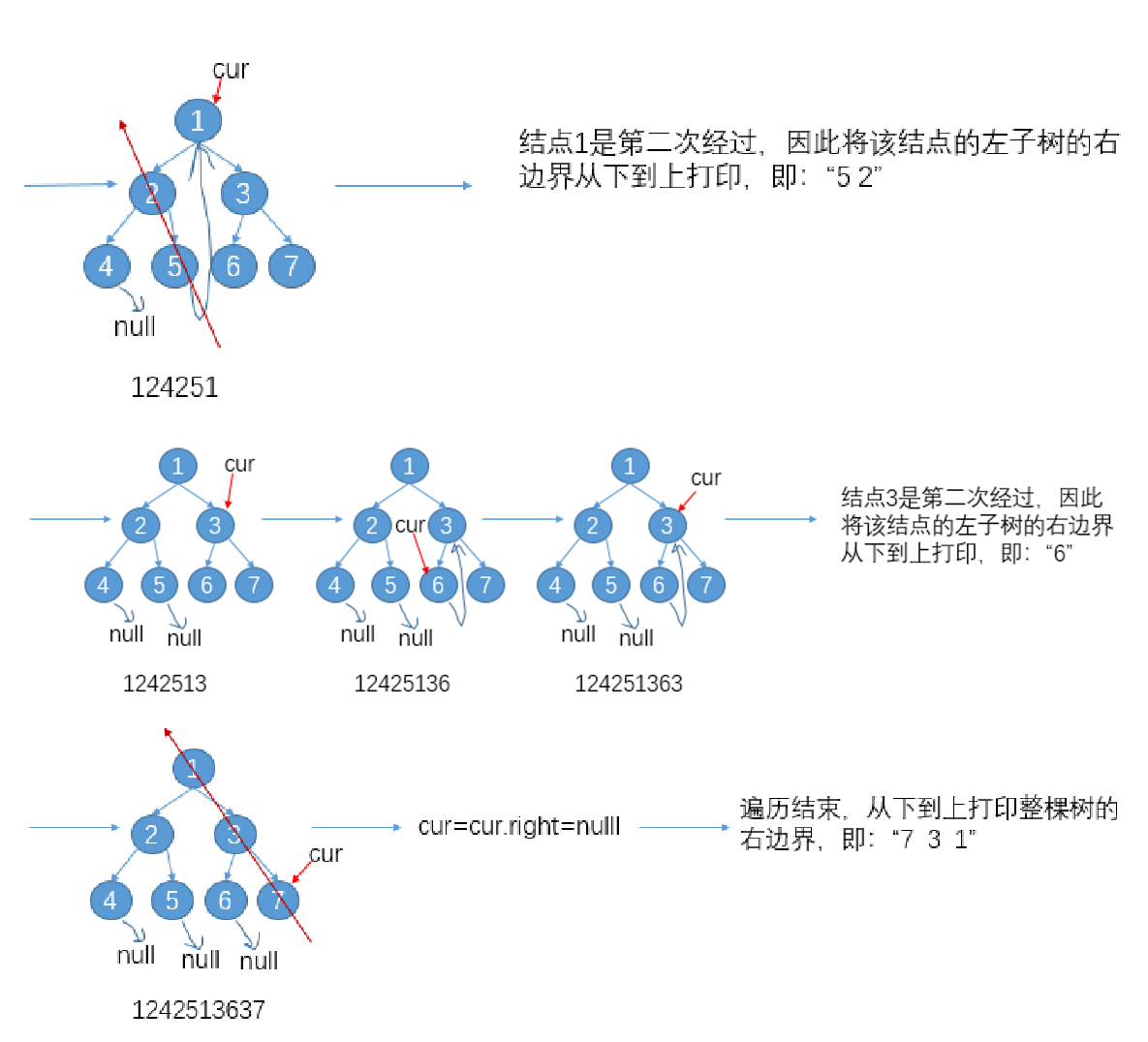
其中无非就是在morris遍历中在第二次经过的结点的时机执行一下打印操作。

而从下到上打印一棵树的右边界，可以将该右边界上的结点看做以 right 指针为后继指针的链表，

然后将其反转reverse，然后打印，最后恢复成原始结构即可

代码如下：

 public static void morrisPos(Node head) {
     // morris后序遍历
     if (head == null) {
         return;
     }
     Node cur = head;
     while (cur != null) {
         if (cur.left == null) {
             cur = cur.right;
         } else {
             Node mostRight = cur.left;
             while (mostRight.right != null && mostRight.right != cur) {
                 mostRight = mostRight.right;
             }
             if (mostRight.right == null) {
                 mostRight.right = cur;
                 cur = cur.left;
             } else {
                 mostRight.right = null;
                 // 在这打印左子树的右边界
                 printRightEdge(cur.left);
                 cur = cur.right;
             }
         }
     }
     // 在这打印整颗树的右边界
     printRightEdge(head);
     System.out.println();
 }

 // 打印节点下左子树的右边界
 private static void printRightEdge(Node root) {
     if (root == null) {
         return;
     }
     // reverse the right edge
     Node cur = root;
     Node pre = null;
     while (cur != null) {
         Node next = cur.right;
         cur.right = pre;
         pre = cur;
         cur = next;
     }
     // print
     cur = pre;
     while (cur != null) {
         System.out.print(cur.value + " ");
         cur = cur.right;
     }
     // recover
     cur = pre;
     pre = null;
     while(cur!=null){
         Node next = cur.right;
         cur.right = pre;
         pre = cur;
         cur = next;
     }
 }

5、morris遍历时间复杂度分析

因为morris遍历中，只有左孩子非空的结点才会经过两次而其它结点只会经过一次，也就是说遍历的次数小于 2N

因此使用morris遍历得到先序、中序序列的时间复杂度自然也是 O(N) ；

但产生后序序列的时间复杂度还要 算上 printRightEdge 的时间复杂度，但是你会发现整个遍历的过程中，所有的

printRightEdge 加起来也只是 遍历并打印了 N 个结点，因此时间复杂度仍然为 O(N)

总结：

morris遍历结点的顺序不是先序、中序、后序，而是按照自己的一套标准来决定接下来要遍历哪个结点

morris遍历的独特之处就是充分利用了叶子结点的无效引用（引用指向的是空，但该引用变量仍然占内存），

从而实现了O(N)的时间复杂度和O(1)的空间复杂度