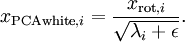UFLDL 教程三总结与答案

主成分分析（PCA）是一种能够极大提升无监督特征学习速度的数据降维算法。更重要的是，理解PCA算法，对实现白化算法有很大的帮助，很多算法都先用白化算法作预处理步骤。这里以处理自然图像为例作解释。

1.计算协方差矩阵：

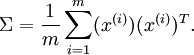  按照通常约束，x为特征变量，上边表示样本数目，下标表示特征数目。这里样本数为m。

xRot = zeros(size(x));
sigma=x*x'/size(x,2);      %sigma为协方差矩阵
[U,S,V]=svd(sigma);        %U为特征向量，X为特征值，V为U的转置,S只有对角线元素非零，为λ1...λn，且它们按照由大到小排序。
xRot = U'*x;               %xRot为将原x

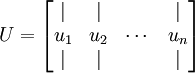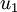.     是主特征向量（对应最大的特征值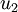）， 是次特征向量。以此类推，另记 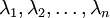为相应的特征值。 

u1...u2为一组基，U*x即将x映射到以U为基的新空间下。

covar = zeros(size(x, 1)); % You need to compute this
sigma1=xRot*xRot'/size(x,2);
[U1,S1,V1]=svd(sigma1);
covar = S1; %S为特征值，只有对角线非零
% Visualise the covariance matrix. You should see a line across the
% diagonal against a blue background.
figure('name','Visualisation of covariance matrix');
imagesc(covar); %验证投影后协方差矩阵计算是否正确

本来可以看到有颜色的对角线，因为这个数据集对角线取值范围原因，无法看到，只能得出左图效果。（The image should show a coloured diagonal line against a blue background. For this dataset, because of the range of the diagonal entries, the diagonal line may not be apparent, so you might get a figure like the one show below）

2.找出主成分个数k

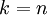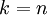既然是降维，如果全部选取主成分则不起到降维作用，例如步骤一中只是将x映射到另一组基所在的空间，并没有减少维数。如何选择 ，即保留多少个PCA主成分？对于高维数据来说，做这个决定就没那么简单：如果 过大，数据压缩率不高，在极限情况 时，等于是在使用原始数据（只是旋转投射到了不同的基）；相反地，如果 过小，那数据的近似误差太太。决定 值时，我们通常会考虑不同 值可保留的方差百分比。具体来说，如果 ，那么我们得到的是对数据的完美近似，也就是保留了100%的方差，即原始数据的所有变化都被保留下来；相反，如果 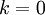，那等于是使用零向量来逼近输入数据，也就是只有0%的方差被保留下来。

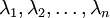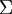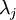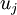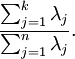一般而言，设 表示 的特征值（按由大到小顺序排列），使得 为对应于特征向量 的特征值。那么如果我们保留前 个成分，则保留的方差百分比可计算为： 即n为所有特征值，取前k项特征值后与全部特征值的比值即为对主成分的保留程度，比值越大保留越多，降维程度越低。

下面设定保留程度为99%，计算k值。

k = ; % Set k accordingly
s=diag(S);
sum_s=sum(s);
lambda=;
for i=:size(s,)
    lambda = lambda+s(i);
    if lambda/sum_s>=0.99         %当所选取特征值之和大于99%则break
        break;
    end
k=i;    %经计算k=88
end

3.降维并对比

通过选取前k项特征值，决定将原图像的维数降至k维。而后将降维后的图像”复原“，与原图对比。

xHat = zeros(size(x));  % You need to compute this
xRot1= U(:,:k)'*x;     %取前k项特征向量与x相乘
xHat = U(:,:k)*xRot1;  %复原

复原的方法：矩阵 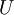有正交性，即满足 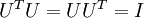，所以若想将旋转后的向量 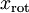还原为原始数据 ，将其左乘矩阵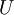即可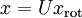： , 验算一下： .

                   

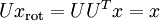原始图像                                                                                                降至k(=88)维后复原

---

4.白化、正则化

我们已经了解了如何使用PCA降低数据维度。在一些算法中还需要一个与之相关的预处理步骤，这个预处理过程称为白化（一些文献中也叫sphering）。举例来说，假设训练数据是图像，由于图像中相邻像素之间具有很强的相关性，所以用于训练时输入是冗余的。白化的目的就是降低输入的冗余性；更正式的说，我们希望通过白化过程使得学习算法的输入具有如下性质：(i)特征之间相关性较低；(ii)所有特征具有相同的方差。

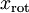协方差矩阵对角元素的值为 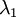和 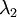绝非偶然。并且非对角元素值为0; 因此, 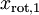和 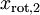是不相关的, 满足我们对白化结果的第一个要求 (特征间相关性降低)。为了使每个输入特征具有单位方差，我们可以直接使用 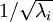作为缩放因子来缩放每个特征 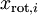。具体地，我们定义白化后的数据 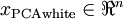如下：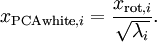

% 这里仅仅是对映射后的特征Xrot进行白化，没有降维！！！
epsilon = 0.1;
xPCAWhite = zeros(size(x));
xPCAWhite = diag(./sqrt(diag(S)+epsilon))*xRot;   %注意这里epsilon不为零，即施加正则化

sigma2=xPCAWhite1*xPCAWhite1'/size(xPCAWhite1,2);
[U2,S2,V2]=svd(sigma2);
covar = S2;
imagesc(covar);     %画图，颜色对角线由红变蓝

对于epsilon的解释：正则化。实践中需要实现PCA白化或ZCA白化时，有时一些特征值 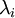在数值上接近于0，这样在缩放步骤时我们除以 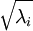将导致除以一个接近0的值；这可能使数据上溢 (赋为大数值)或造成数值不稳定。因而在实践中，我们使用少量的正则化实现这个缩放过程，即在取平方根和倒数之前给特征值加上一个很小的常数 ：

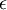当 在区间 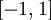上时, 一般取值为 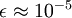。对图像来说, 这里加上 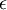，对输入图像也有一些平滑(或低通滤波)的作用。这样处理还能消除在图像的像素信息获取过程中产生的噪声，改善学习到的特征。

%这里仅仅是对映射后的特征xRot进行白化，没有降维！！！
epsilon=0;
xPCAWhite1 = diag(./sqrt(diag(S)+epsilon))*xRot;   %注意这里额epsilon为零，即没有施加正则化
sigma2=xPCAWhite1*xPCAWhite1'/size(xPCAWhite1,2);
[U2,S2,V2]=svd(sigma2);
covar = S2;
imagesc(covar);     %画图：颜色对角线全红

那么问题来了，正则化与否有什么区别呢???原文这样写：PCA whitening without regularisation results a covariance matrix that is equal to the identity matrix. PCA whitening with regularisation results in a covariance matrix with diagonal entries starting close to 1 and gradually becoming smaller.意思是：不经正则化的PCA白化得到的特征矩阵S等价于单位阵，即代码[U,S,V]中的S。(文中是说特征矩阵，但是只有对角线非零的矩阵只有特征矩阵)；而经过正则化的PCA白化得到的特征矩阵对角线元素的值由近似1逐渐下降。文中给出区别：前者的S在图中为蓝色背景下一条红色的对角线（you should see a red line across the diagonal (one entries against a blue background），后者的S在图像中表现为红色由对角线渐变为蓝色（you should see a red line that slowly turns blue across the diagonal）。上图：

      

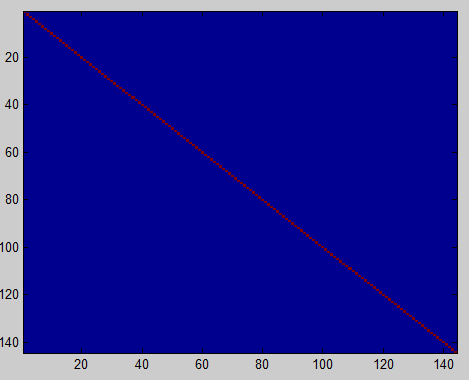
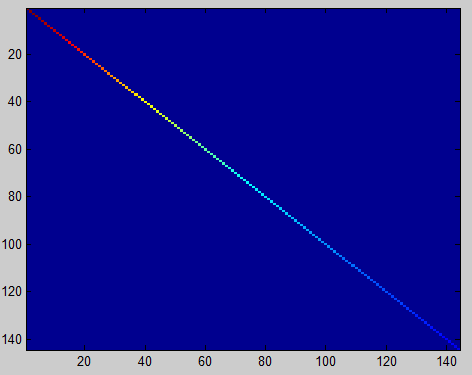
不经过正则化的PCA白化                                                                               经过正则化的PCA白化

     白化与降维相结合。 如果你想要得到经过白化后的数据，并且比初始输入维数更低,可以仅保留 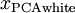中前 个成分。当我们把PCA白化和正则化结合起来时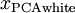， 中最后的少量成分将总是接近于0，因而舍弃这些成分不会带来很大的问题。 上文已经提到过了，上文只是白化，没有降维，而当我们向将白化与降维结合时，要正则化，因为此时特征值S中最后的少量成分将减小至零。

5.ZCA白化

经过PCA白化(不经过正则化)后，数据现在的协方差矩阵为单位矩阵 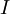。我们说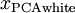， 是数据经过PCA白化后的版本: 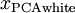中不同的特征之间不相关并且具有单位方差。要说明的是，使数据的协方差矩阵变为单位矩阵 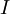的方式并不唯一。具体地，如果 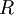是任意正交矩阵，即满足 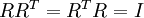(说它正交不太严格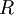， 可以是旋转或反射矩阵), 那么 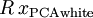仍然具有单位协方差。在ZCA白化中，令 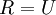。我们定义ZCA白化的结果为：。

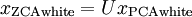当使用 ZCA白化时(不同于 PCA白化)，我们通常保留数据的全部 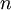个维度，不尝试去降低它的维数。 

xZCAWhite = zeros(size(x));
epsilon = 0.1;
xZCAWhite = U*diag(./sqrt(diag(S)+epsilon))*U'*x;
%经过ZCA白化与原图对比
figure('name','ZCA whitened images');
display_network(xZCAWhite(:,randsel));
figure('name','Raw images');
display_network(x(:,randsel));

       

原图                                                                                     经过ZCA白化

You should observe that whitening results in, among other things, enhanced edges.  边缘增强。