G711算法学习

采样和量化

首先需要明确的两个概念，“采样”和“量化”。对于给定的一个波形，采样是从时间上将连续变成离散的过程，而采样得到的值，可能还是不能够用给定的位宽（比如8bit）来表示，这就需要经过量化，即从我们能够表示的离散值里面找一个跟采样值接近的值，近似地表示它。

一般来说，量化是模拟音频到数字音频（PCM）过程中产生误差的唯一一个地方。

下面我们举个例子来说明，首先用matlab生成一个正弦波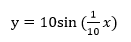，，由于，所以这个波形的周期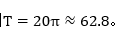

然后以20的采样周期采样得到图上的16个蓝色点。

[0, 9.092974268, -7.568024953, -2.794154982, 9.893582466, -5.440211109, -5.36572918, 9.906073557, -2.879033167, -7.509872468, 9.129452507, -0.088513093, -9.05578362, 7.625584505, 2.709057883, -9.880316241]

这些小数存储时要占用大量的空间，因此我们要通过量化，将其舍入到近似的整数，这样采样值就能用一个±16范围的整数来存储（5bit）。

 x=::;
 y=*sin(x/);
 plot(x,y,'r')
 axis([,,-,]);
 set(gca, 'XTickMode','manual','XTick',[::]);
 set(gca,'YTickMode','manual','YTick',[-::]);grid
 hold on
 a=::;
 b=*sin(a/);
 plot(a,b,'*')

以上就是一个简单的采样和量化过程。

根据采样定理，用大于信号最高频率两倍的频率，对周期信号进行采样，可以保证完全重构原始信号。由于G711主要用于传递话音，而人声最大频率一般在3.4kHz，所以只要以8k的采样频率对人声进行采样，就可以保证完全还原原始声音。

而人耳朵能够感知的声音频率在20kHz范围内，所以只要以大于40kHz频率采样，就可以完全重建原始声音。我们常常能见到44.1kHz采样的音乐文件，甚至更高采样频率，也是由于这个道理。之所以会取一个大于40k的采样频率比如44.1k、48k甚至更高的96k，我认为有以下几个原因：

1）实际音频的频谱不是带宽限制的，在带外还有高频信号。因此我们需要先经过一个低通滤波器将高频信号滤掉。而实际的低通滤波器不是完整的在截止频率将信号截断，而是一个很陡峭的曲线，所以留出了一些余量保证滤除带外信号后不影响带内信号。

2）采样之后需要经过量化，这带来了一些误差，重建出来的音频和原始的模拟音频有微小区别，通过增加量化深度或者采样频率能减少这种误差。

3）实际的采样窗口不是无限长的，加窗操作引入了一些大于奈奎斯特频率的信号，导致频率出现了混叠，影响了原始信号的恢复值。

4）在音频制作过程中采用96k、192k甚至更高，可以满足一些后期处理的需要。而播放端播放96k的音频未必会比44.1k有更好的效果，两者的区别可能更多来自于前3条的原因。

G711压扩算法

G711算法采用8kHz采样率，有A-law和μ-law两种压扩方式，分别是将13bit和14bit编码为8bit，因此G711固定码率是8kHz*8bit=64kbps。两者都是对数变换，A-law更加方便计算机处理。μ-law提供了略微高一些的动态范围，但代价是对于弱信号的量化误差相对A-law高一些。两者均采用对数变换的原因也正是由于人耳对于声音的感知不是线性变化而是对数型变化的特性。

下面分别介绍两种算法。

A-law的公式如下，一般采用A=87.6

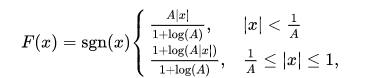
画出图来则是如下图，用x表示输入的采样值，F(x)表示通过A-law变换后的采样值，y是对F(x)进行量化后的采样值。

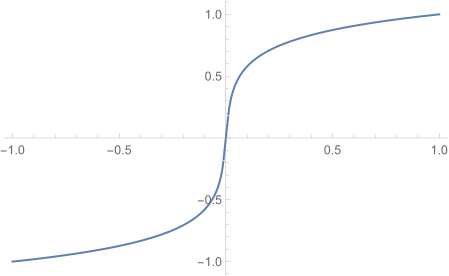
由此可见在输入的x为高值的时候，F(x)的变化是缓慢的，有较大范围的x对应的F(x)最终被量化为同一个y，精度较低。相反在低声强区域，也就是x为低值的时候，F(x)的变化很剧烈，有较少的不同x对应的F(x)被量化为同一个y。意思就是说在声音比较小的区域，精度较高，便于区分，而声音比较大的区域，精度不是那么高。

μ-law的公式如下，μ取值一般为255

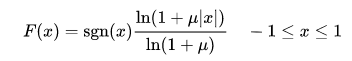
和A-law画在同一个坐标轴中就能发现A-law在低强度信号下，精度要稍微高一些。

以上是两种算法的连续条件下的计算公式，实际应用中，我们确实可以用浮点数计算的方式把F(x)结果计算出来，然后进行量化，但是这样一来计算量会比较大，实际上对于A-law（A=87.6时），是采用13折线近似的方式来计算的，而μ-law（μ=255时）则是15段折线近似的方式。

A-law如下表计算，第一列是采样点，共13bit，最高位为符号位。对于前两行，折线斜率均为1/2，跟负半段的相应区域位于同一段折线上，对于3到8行，斜率分别是1/4到1/128，共6段折线，加上负半段对应的6段折线，总共13段折线，这就是所谓的A-law十三段折线法

对应的解码公式则是

网上有G711的源码，我们可以从中学到一些东西。

 #define    SIGN_BIT    (0x80)        /* Sign bit for a A-law byte. */
 #define    QUANT_MASK    (0xf)        /* Quantization field mask. */
 #define    NSEGS        (8)            /* Number of A-law segments. */
 #define    SEG_SHIFT    (4)            /* Left shift for segment number. */
 #define    SEG_MASK    (0x70)        /* Segment field mask. */
 #define    BIAS        (0x84)        /* Bias for linear code. */

 static const int16_t seg_uend[] = { 0xFF, 0x1FF, 0x3FF, 0x7FF, 0xFFF, 0x1FFF, 0x3FFF, 0x7FFF };
 static const int16_t seg_aend[] = { 0x1F, 0x3F, 0x7F, 0xFF, 0x1FF, 0x3FF, 0x7FF, 0xFFF };;

 static int16_t search(int16_t val, const int16_t *table, int16_t    size)
 {
     int    i;

     for (i = ; i < size; i++) {
         if (val <= *table++)
             return (i);
     }
     return (size);
 }

 static uint8_t linear2alaw(int16_t pcm_val) /* 2's complement (16-bit range) */
 {
     int16_t  mask;
     int16_t  seg;
     uint8_t  aval;

     pcm_val = pcm_val >> ;//这里右移3位，因为采样值是16bit，而A-law是13bit数据，存储在高13位上，低3位被舍弃

     if (pcm_val >= ) {
         mask = 0xD5;//二进制的11010101
     }
     else {
         mask = 0x55;//二进制的01010101，与0xD5只有符号位的不同
         pcm_val = -pcm_val - ;//负数转换为正数计算
     }

     seg = search(pcm_val, seg_aend, );//查找采样值对应哪一段折线

     if (seg >= ) {
         return (uint8_t)(0x7F);//越界时直接返回最大值
     }
     else {
         //以下按照表格处理，低4位是数据，5~7位是指数，最高位是符号
         aval = (uint8_t)seg << SEG_SHIFT;
         if (seg < )
             aval |= (pcm_val >> ) & QUANT_MASK;
         else
             aval |= (pcm_val >> seg) & QUANT_MASK;

         return (aval);
     }
 }

跟算法相关的部分我已经在注释中说明了，这里令人困惑的一点是mask的作用，为此我把输入x从-32768~32767范围内的所有输出值对应标在坐标格上（图一左半边应该是在0坐标以下，为表示方便取了其绝对值）

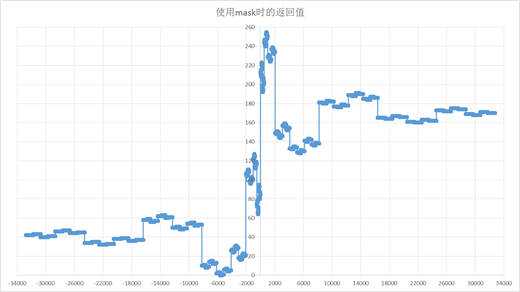
对比两张图可以发现不使用mask的时候就是原始的A-law压扩算法的13段折线。而使用mask则把结果重新进行了排布。这样做的好处是

1、结果都是正数，最高位取反是原来的符号位

2、mask实际上是异或操作，mask的奇数位是1，偶数位是0，异或操作是对奇数位取反，偶数位保留，还原时只需要再次异或0x55即可

3、将奇偶数位进行不同的操作，防止相邻干扰（但后来看到u-law并没有这样的情况，所以暂时存疑，可能只是一种为计算机优化的策略）

相应的解码函数如下（加0x8那里是经常会有的尾数+0.5操作，是一种四舍五入的方法）：

 static int16_t alaw2linear(uint8_t a_val)
 {
     int16_t    t;
     int16_t    seg;

     a_val ^= 0x55;//异或操作把mask还原

     t = (a_val & QUANT_MASK) << ;//取低4位，即上表中的abcd值，然后左移4位变成abcd0000
     seg = ((unsigned)a_val & SEG_MASK) >> SEG_SHIFT;//取中间3位，指数部分
     switch (seg)
     {
     case ://表中第一行，abcd0000 -> abcd1000
         t += ;
         break;
     case ://表中第二行，abcd0000 -> 1abcd1000
         t += 0x108;
         break;
     default://表中其他行，abcd0000 -> 1abcd1000 的基础上继续左移
         t += 0x108;
         t <<= seg - ;
         break;
     }
     return ((a_val & SIGN_BIT) ? t : -t);
 }

相应的μ-law的计算方法如下表。

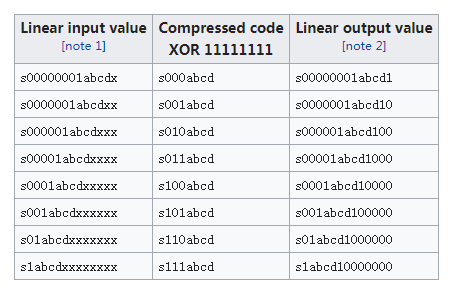
本质上跟A-law的区别不大

u-law计算时先用0x84 - sample（小于0）或者sample + 0x84，然后对应每一段使用不同的移位值得到最终的8bit结果，画图如下。解码是上述过程的反方向，代码比A-law简单好理解。

 static int16_t ulaw2linear(uint8_t u_val)
 {
     int16_t    t;

     /* Complement to obtain normal u-law value. */
     u_val = ~u_val;

     /*
     * Extract and bias the quantization bits. Then
     * shift up by the segment number and subtract out the bias.
     */

     t = ((u_val & QUANT_MASK) << ) + BIAS;
     t <<= ((unsigned)u_val & SEG_MASK) >> SEG_SHIFT;

     return ((u_val & SIGN_BIT) ? (BIAS - t) : (t - BIAS));
 }

 static uint8_t linear2ulaw(int16_t pcm_val)    /* 2's complement (16-bit range) */
 {
     int16_t        mask;
     int16_t        seg;
     uint8_t        uval;

     /* Get the sign and the magnitude of the value. */
     if (pcm_val < ) {
         pcm_val = BIAS - pcm_val;
         mask = 0x7F;
     }
     else {
         pcm_val += BIAS;
         mask = 0xFF;
     }

     /* Convert the scaled magnitude to segment number. */
     seg = search(pcm_val, seg_uend, );

     /*
     * Combine the sign, segment, quantization bits;
     * and complement the code word.
     */
     if (seg >= )        /* out of range, return maximum value. */
         return (0x7F ^ mask);
     else {
         uval = (seg << ) | ((pcm_val >> (seg + )) & 0xF);
         return (uval ^ mask);
     }
 }

代码里还有ulaw和alaw互相转换的函数，由于两者都是8bit，去除符号位就是128个值，直接用数组映射就实现了a-u互相转换，这样时间复杂度只有O(1)

总结

G711尽管是一种非常古老的话音编码算法，原理和计算也比较简单，但是其中用到的一些基本原理同样在其他编码算法中得到了应用，对其进行深入的了解有助于更好的理解其他的算法。

源代码中关于移位运算，掩码运算，我还不是完全的理解，只能根据自己的经验进行一些猜测，之后会继续学习，希望对这方面能有更深入的认识。

采样和量化是编解码的基础知识，因此也对此进行了区分和强调。

主要参考文献：

1、英文wiki的G711词条，里面有对该算法的详细描述

2、G711的标准算法源代码，代码利用了移位运算等进行了加速，比原始的浮点计算方式更快，适用于嵌入式设备等性能较为低下的设备。

https://github.com/quatanium/foscam-ios-sdk/blob/master/g726lib/g711.c