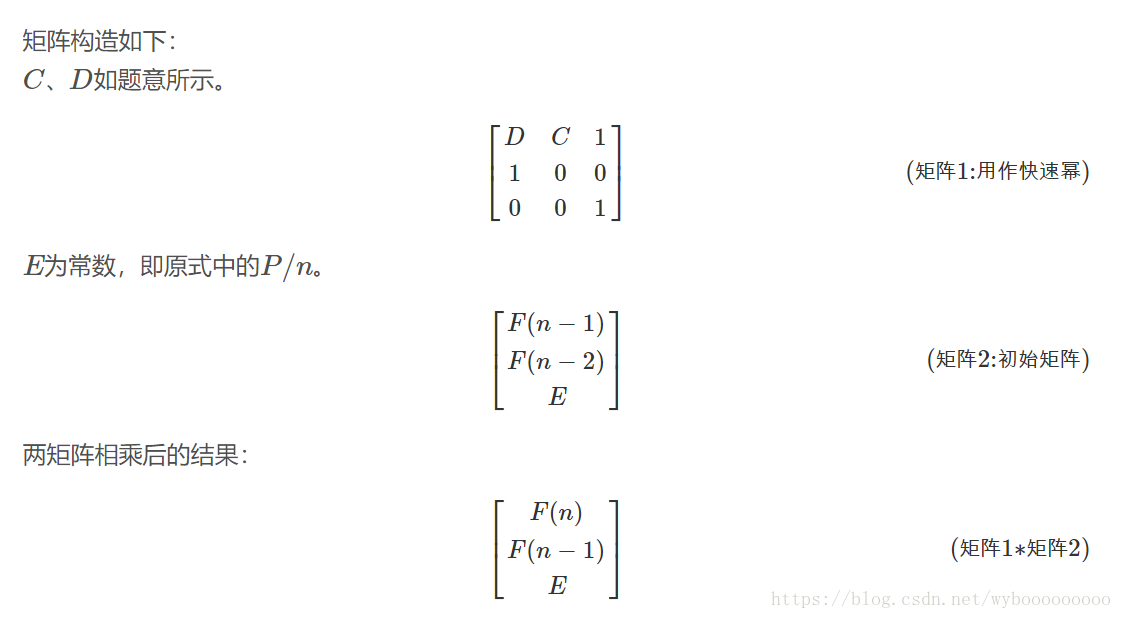hdu 6395Sequence【矩阵快速幂】【分块】
Sequence
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 1951 Accepted Submission(s): 750
Problem Description
Let us define a sequence as below
⎧⎩⎨⎪⎪⎪⎪⎪⎪F1F2Fn===ABC⋅Fn−2+D⋅Fn−1+⌊Pn⌋
Your job is simple, for each task, you should output Fn module 109+7.
Input
The first line has only one integer T, indicates the number of tasks.
Then, for the next T lines, each line consists of 6 integers, A , B, C, D, P, n.
1≤T≤200≤A,B,C,D≤1091≤P,n≤109
Sample Input
2 3 3 2 1 3 5 3 2 2 2 1 4
Sample Output
36 24
Source
2018 Multi-University Training Contest 7
Recommend
chendu | We have carefully selected several similar problems for you: 6408 6407 6406 6405 6404
学习了一个新的递推求数的方法
通过构造矩阵 用矩阵递推 用矩阵快速幂优化 可以用来求一个随机的很大的数的值
矩阵快速幂的写法 O(logn)

这道题还有一点特别的是 后面的常数项是会变化的 但是他是分段的
所以就分块的来求 因为要知道乘的次数所以每次要求一下这个区间有多少个数
c++TLE g++AC
#include<iostream>
#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<stack>
#define inf 1e18
using namespace std;
long long t, a, b, c, d, p, n;
const int mod = 1e9 + 7;
struct mat{
long long m[3][3];
mat(){
memset(m, 0, sizeof(m));
}
void init()
{
memset(m, 0, sizeof(m));
for(int i = 0; i < 3; i++){
m[i][i] = 1;
}
}
friend mat operator * (mat a, mat b)
{
mat c;
for(int i = 0; i < 3; i++){
for(int j = 0; j < 3; j++){
for(int k = 0; k < 3; k++){
c.m[i][j] += a.m[i][k] * b.m[k][j];
c.m[i][j] %= mod;
}
}
}
return c;
}
};
mat pow_mat(mat a, int b)
{
mat c;
c.init();
while(b){
if(b & 1){
c = c * a;
}
a = a * a;
b >>= 1;
}
return c;
}
int main()
{
scanf("%lld", &t);
while(t--){
scanf("%lld%lld%lld%lld%lld%lld", &a, &b, &c, &d, &p, &n);
if(n == 1){
printf("%lld\n", a);
continue;
}
mat f;
f.m[0][0] = d;
f.m[1][0] = c;
f.m[2][0] = f.m[0][1] = f.m[2][2] = 1;
mat g;
g.m[0][0] = b;
g.m[0][1] = a;
if(p >= n){
for(long long i = 3, j; i <= n; i = j + 1){
j = p / (p / i);//个数
g.m[0][2] = p / i;
mat po = pow_mat(f, min(j - i + 1, n - i + 1));
g = g * po;
}
}
else{
for(long long i = 3, j; i <= p; i = j + 1){
j = p / (p / i);
g.m[0][2] = p / i;
mat po = pow_mat(f, j - i + 1);
g = g * po;
}
mat po;
g.m[0][2] = 0;
if(p < 3){
po = pow_mat(f, n - 2);
}
else{
po = pow_mat(f, n - p);
}
g = g * po;
}
printf("%lld\n", g.m[0][0]);
}
return 0;
}
hdu 6395Sequence【矩阵快速幂】【分块】的更多相关文章
- HDU 2855 (矩阵快速幂)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=2855 题目大意:求$S(n)=\sum_{k=0}^{n}C_{n}^{k}Fibonacci(k)$ ...
- HDU 4471 矩阵快速幂 Homework
题目链接: http://acm.hdu.edu.cn/showproblem.php?pid=4471 解题思路,矩阵快速幂····特殊点特殊处理····· 令h为计算某个数最多须知前h个数,于是写 ...
- hdu6395 (矩阵快速幂+分块)
Online Judge Online Exercise Online Teaching Online Contests Exercise Author F.A.Q Hand In Hand Onli ...
- HDU - 1575——矩阵快速幂问题
HDU - 1575 题目: A为一个方阵,则Tr A表示A的迹(就是主对角线上各项的和),现要求Tr(A^k)%9973. Input数据的第一行是一个T,表示有T组数据. 每组数据的第一行有n( ...
- hdu 1757 (矩阵快速幂) 一个简单的问题 一个简单的开始
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1757 题意不难理解,当x小于10的时候,数列f(x)=x,当x大于等于10的时候f(x) = a0 * ...
- 随手练——HDU 5015 矩阵快速幂
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=5015 看到这个限时,我就知道这题不简单~~矩阵快速幂,找递推关系 我们假设第一列为: 23 a1 a2 ...
- HDU 3802 矩阵快速幂 化简递推式子 加一点点二次剩余知识
求$G(a,b,n,p) = (a^{\frac {p-1}{2}}+1)(b^{\frac{p-1}{2}}+1)[(\sqrt{a} + \sqrt{b})^{2F_n} + (\sqrt{a} ...
- How many ways?? HDU - 2157 矩阵快速幂
题目描述 春天到了, HDU校园里开满了花, 姹紫嫣红, 非常美丽. 葱头是个爱花的人, 看着校花校草竞相开放, 漫步校园, 心情也变得舒畅. 为了多看看这迷人的校园, 葱头决定, 每次上课都走不同的 ...
- HDU 5950 矩阵快速幂
Recursive sequence Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Other ...
- hdu 1757 矩阵快速幂 **
一看正确率这么高,以为是水题可以爽一发,结果是没怎么用过的矩阵快速幂,233 题解链接:点我 #include<iostream> #include<cstring> ; us ...
随机推荐
- nginx配置设置,使部分页面访问跳转到404页面
location ~* /(ask|hospital|wenda|regsearch|user|doctor) { return ; } error_page /.html;
- SpringBoot------8080端口被占用抛出异常
异常信息: The Tomcat connector configured to listen on port failed to start. The port may already be in ...
- Java 流(Stream)、文件(File)和IO -- Java ByteArrayOutputStream类
Java ByteArrayOutputStream类 字节数组输出流在内存中创建一个字节数组缓冲区,所有发送到输出流的数据保存在该字节数组缓冲区中.创建字节数组输出流对象有以下几种方式. 下面的构造 ...
- 【Ubuntu】Windows 远程桌面连接ubuntu及xrdp的一些小问题(远程桌面闪退、连接失败、tab补全功能,无菜单栏,error - problem connecting )【转】
转:https://blog.csdn.net/u014447845/article/details/80291678 1.远程桌面闪退,shell可以用的问题:(1)需要在该用户目录创建一个.xse ...
- 【ArcGIS】ArcGIS Android SDK
1.错误提示 11-06 18:12:17.553: A/libc(11929): Fatal signal 11 (SIGSEGV), code 1, fault addr 0x0 in tid 1 ...
- centos 7 安装 gcc-4.9.3.tar.gz
由于编译新内核需要,更新了GCC编译器,自行获取文件,手动升级. 首先是获取文件:wget http://ftp.tsukuba.wide.ad.jp/software/gcc/releases/gc ...
- Selenium 延时等待
在 Selenium 中, get() 方法会在网页框架加载结束后结束执行,此时如果获取 page_source ,可能并不是浏览器完全加载完成的页面: 如果某些页面有额外的 Ajax 请求,我们在网 ...
- CMake设置输出目录
set(CMAKE_ARCHIVE_OUTPUT_DIRECTORY ${CMAKE_BINARY_DIR}/Lib)set(CMAKE_LIBRARY_OUTPUT_DIRECTORY ${CMAK ...
- mysql错误:got error 28 from storage engine
今天碰到数据库出错 Got error 28 from storage engine 查了一下,数据库文件所在的盘应该没事,应该是数据库用的临时目录空间不够 引用 磁盘临时空间不够导致.解决办法:清空 ...
- Android学习之PopupWindow
Android的对话框有两种:PopupWindow和AlertDialog. 详细说明如下: AlertDialog是非阻塞式对话框:AlertDialog弹出时,后台还可以做事情: AlertDi ...