3D-2D透视投影数学推导
请尊重作者,禁止私自盗用图片!
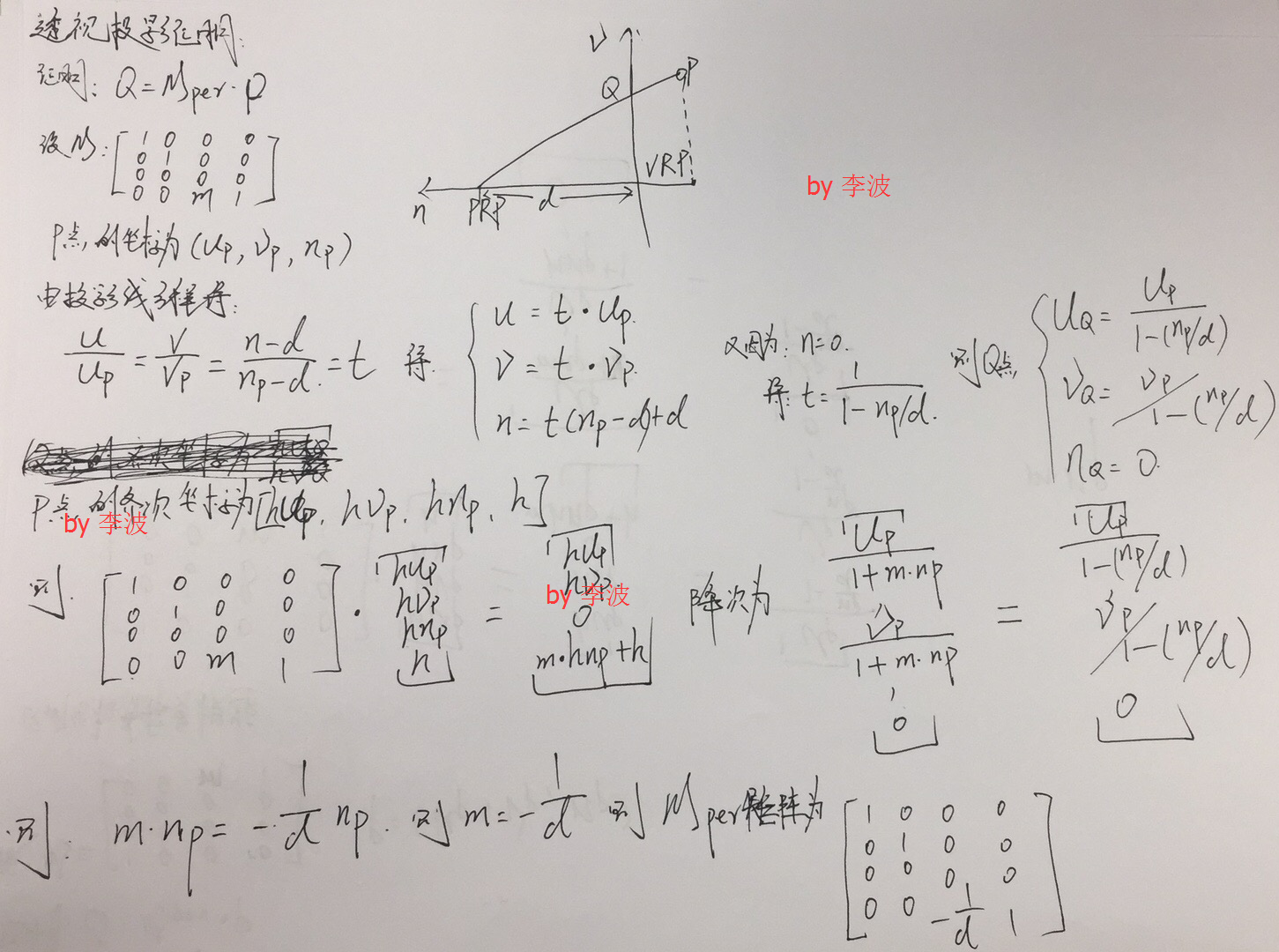
3D-2D透视投影数学推导的更多相关文章
- 【转载】3D/2D中的D3DXMatrixPerspectiveFovLH和D3DXMatrixOrthoLH投影函数详解
原文:3D/2D中的D3DXMatrixPerspectiveFovLH和D3DXMatrixOrthoLH投影函数详解 3D中z值会影响屏幕坐标系到世界坐标系之间的转换,2D中Z值不会产生影响(而只 ...
- 借One-Class-SVM回顾SMO在SVM中的数学推导--记录毕业论文5
上篇记录了一些决策树算法,这篇是借OC-SVM填回SMO在SVM中的数学推导这个坑. 参考文献: http://research.microsoft.com/pubs/69644/tr-98-14.p ...
- 关于不同进制数之间转换的数学推导【Written By KillerLegend】
关于不同进制数之间转换的数学推导 涉及范围:正整数范围内二进制(Binary),八进制(Octonary),十进制(Decimal),十六进制(hexadecimal)之间的转换 数的进制有多种,比如 ...
- UVA - 10014 - Simple calculations (经典的数学推导题!!)
UVA - 10014 Simple calculations Time Limit: 3000MS Memory Limit: Unknown 64bit IO Format: %lld & ...
- 『sumdiv 数学推导 分治』
sumdiv(POJ 1845) Description 给定两个自然数A和B,S为A^B的所有正整数约数和,编程输出S mod 9901的结果. Input Format 只有一行,两个用空格隔开的 ...
- LDA-线性判别分析(二)Two-classes 情形的数学推导
本来是要调研 Latent Dirichlet Allocation 的那个 LDA 的, 没想到查到很多关于 Linear Discriminant Analysis 这个 LDA 的资料.初步看了 ...
- leetcode 343. Integer Break(dp或数学推导)
Given a positive integer n, break it into the sum of at least two positive integers and maximize the ...
- [hdu5307] He is Flying [FFT+数学推导]
题面 传送门 思路 看到这道题,我的第一想法是前缀和瞎搞,说不定能$O\left(n\right)$? 事实证明我的确是瞎扯...... 题目中的提示 这道题的数据中告诉了我们: $sum\left( ...
- ZOJ3329(数学推导+期望递推)
要点: 1.期望的套路,要求n以上的期望,则设dp[i]为i分距离终点的期望步数,则终点dp值为0,答案是dp[0]. 2.此题主要在于数学推导,一方面是要写出dp[i] = 什么,虽然一大串但是思维 ...
随机推荐
- java 多个数 组合成不同的组
public static Stack<Integer> stack = new Stack<Integer>(); private static List<String ...
- 手撕面试官系列(二):开源框架面试题Spring+SpringMVC+MyBatis
文章首发于今日头条:https://www.toutiao.com/i6712324863006081549/ 前言 跳槽时时刻刻都在发生,但是我建议大家跳槽之前,先想清楚为什么要跳槽.切不可跟风,看 ...
- Linux04 目录的相关操作(mkdir、rmdir、rm、cp)
一.创建目录:mkdir mkdir 目录名 二.删除目录:rmdir / rm rmdir 目录名 rm -r 目录名 每一级子目录都会询问是否删除 rm -rf 目录名 慎用,给 ...
- github中的各种操作
1.上传文件到github 如图,你现在有三个项目在一个文件夹中,我们要把它上传到自己的github仓库中,该怎么做呢? 1.首先右击空白处,点击Git Bash Here,出现命令行 2. git ...
- 11 IO流(八)——装饰器设计模式,Filter装饰流
声明:本文部分图片及内容引用自:https://www.cnblogs.com/qiumingcheng/p/5219631.html java装饰器设计模式 举一个形象的例子,人可以说话,而扩音器可 ...
- Pair(二进制处理+数位dp)(2019牛客暑期多校训练营(第七场))
示例: 输入: 33 4 24 5 27 8 5 输出:5 7 31 题意:存在多少对<x,y>满足x&y>C或x^y<C的条件.(0<x<=A,0< ...
- 『Go基础』第7节 变量
1. 什么是变量? 我们应该怎么去理解变量? 在这里我要举一个例子: 大家应该都知道王者荣耀这个游戏. 当我们在玩王者荣耀的时候, 我们操控的英雄的血量是不断变化的, 这个血量是存在内存中的. 那么这 ...
- Java多线程编程之读写锁【ReentrantReadWriteLock】
有时候我们需要有这样的需求: 对于同一个文件进行读和写操作,普通的锁是互斥的,这样读的时候会加锁,只能单线程的读,我们希望多线程的进行读操作,并且读的时候不能进行写操作,写的时候不能进行 ...
- node.js开发 npm包管理工具
npm介绍 说明:npm(node package manager)是nodejs的包管理器,用于node插件管理(包括安装.卸载.管理依赖等) 使用npm安装插件:命令提示符执行npm instal ...
- 【转载】 C#中使用CopyTo方法将List集合元素拷贝到数组Array中
在C#的List集合操作中,有时候需要将List元素对象拷贝存放到对应的数组Array中,此时就可以使用到List集合的CopyTo方法来实现,CopyTo方法是List集合的扩展方法,共有3个重载方 ...
