长乐国庆集训Day5-2

T1 彩虹

题目

【题目描述】

Mr.Raju和他的一个大家庭外出度假，他们想要乘着彩虹欣赏周围的景色，但是这样最会有一些问题。

在他们家族中，如果一个人想要骑上彩虹，那么他喜欢的所有人和喜欢他的所有人都必须一同骑上彩虹。如果一个人没有喜欢的人，也没有人喜欢他，那么他也可以乘上彩虹。

你被请来解决这个难题，我们会提供给你家族所有成员的体重，以及每个人喜欢的人的列表，同样给出的还有彩虹能承受的总重量，你需要计算出在以上条件下彩虹所能承载的最多人数。

为了方便描述，所有的家庭成员都被标号，从1到n。

【输入格式】

有多组数据，每组数据之间有一空行。

对于每一组数据，第一行为整数n(1≤n≤1000)和c(0≤c≤1000),n表示家庭成员的总人数，c表示彩虹的承载量。

第二行为n个数为1到n个家庭成员的体重（体重是1000以内的正整数）。

接下来n行，每行第一个数k[i]表示第i个人有多少喜欢的人，接下来k[i]个整数为他喜欢的人的编号。

当n=0，c=0是表示数据结束。保证数据组数不超过3。

【输出格式】

对于每一组数据，输出可以同时骑彩虹的最大人数。（输出的每个答案之间不要空行）。

【输入样例】

【输出样例】

【数据规模】

对于20%的数据：n≤8；

对于100%的数据：n,c≤1000。

解析

先用并查集将每个人与其喜欢的人合并起来，计算他们的总重量与总人数。

再跑一遍01背包即可。

Code

#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <cstdio>
#include <cmath>
using namespace std;
int read()
{
    int num=,w=;
    char ch=getchar();
    while(ch<''||ch>'')
    {
        if(ch=='-') w=-;
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        num=(num<<)+(num<<)+ch-'';
        ch=getchar();
    }
    return num*w;
}
const int N=;
int n,C,a[N],b[N],c[N],fa[N],f[N],maxn;
int get(int x)
{
    if(fa[x]==x) return x;
    return fa[x]=get(fa[x]);
}
int main()
{
    //freopen("rainbow.in","r",stdin);
    //freopen("rainbow.out","w",stdout);
    while()
    {
        n=read(),C=read(),maxn=;
        if(n==&&C==) break;
        memset(f,,sizeof(f));
        for(int i=;i<=n;i++) a[i]=read(),b[i]=,c[i]=,fa[i]=i;
        for(int i=;i<=n;i++)
        {
            int k=read();
            for(int j=;j<=k;j++)
            {
                int x=read();
                fa[get(i)]=get(x);
            }
        }
        for(int i=;i<=n;i++)
        {
            int temp=get(i);
            b[temp]+=a[i],c[temp]++;
        }
        for(int i=;i<=n;i++)
            if(b[i]!=)
                for(int j=C;j>=b[i];j--) f[j]=max(f[j],f[j-b[i]]+c[i]);
        for(int i=;i<=C;i++) maxn=max(maxn,f[i]);
        cout<<maxn<<endl;
    }
    return ;
}

T2 红十字

题目

【题目描述】

通往藏宝库的通道打开了，走下一段长长的楼梯，钻过一条矮矮的地道，你和小可可终于来到了藏宝库的门前。随之而来的就是最后一个挑战，只要能打开宝库的门，里面的宝藏就是你们的了。

宝库的门依然是通过机关打开，这个门很奇怪，是一个正方形，被划分成许多大小一致的正方形的小方格，这些方格不是红色就是白色，猛看上去这些方格组成了许多红十字状的标志。根据藏宝图记载，只要找到门上最大的红十字，按下它中心的方格，宝库的门就能打开了。

红十字标志也是一个正方形，边长为(2k+1)*(2k+1)，其中k为非负整数。它的四条边与门的边平行，而且恰由门上的(2k+1)*(2k+1)个小方格组成。这里，红十字标志是以白色为底色，红色为十字的颜色。假设用1表示红色，用0表示白色。对应到计算机处理的数据中，就是除了正中列与正中行全为1外，其余方格均为0。

以下是几种不同大小的标志：

1*1:

1

3*3

010

111

010

5*5

00100

00100

11111

00100

00100

小可可被这个机关难到了，现在只有靠你了，请你帮助他在这个门上找到一个最大的红十字标志，输出它的边长即可。

【输入格式】

本题输入量巨大，推荐使用以下输入方法：

scanf("%d\n", &n);

for (i = 1; i<= n; i++) scanf("%s", s[i] + 1);

for (i = 1; i<= n; i++)

for (j = 1; j <= n; j++)

a[i][j] = s[i][j] - '0';

其中n是宝库的门的边长，s是字符数组，a[i][j]是第i行第j列的数值。

【输出格式】

对于每个询问输出一行表示答案。

【输入样例】

【输出样例】

【数据规模】

对于30%的数据，n≤100。

对于50%的数据，n≤500。

对于100%的数据，n≤2000。

解析

用sum纪录子矩阵的值。

对于以(x,y)为中心且长度为k的矩阵，如果是红十字，那么以(x,y)为中心且长度为k-2(k>=3)的矩阵必然也是红十字。

所以可以枚举红十字的中心，求出以(x,y)为中心的最大红十字的边长，具体可以用二分实现。

Code

#include<bits/stdc++.h>
using namespace std;
const int N=;
int n,a[N][N],sum[N][N],ans;
char s[N][N];
int dfs(int lx,int ly,int rx,int ry)
{
    return sum[rx][ry]+sum[lx-][ly-]-sum[lx-][ry]-sum[rx][ly-];
}
int main()
{
    scanf("%d\n",&n);
    for(int i=;i<=n;i++)  scanf("%s",s[i]+);
    for(int i=;i<=n;i++)
        for(int j=;j<=n;j++) a[i][j]=s[i][j]-'',sum[i][j]=sum[i-][j]+sum[i][j-]-sum[i-][j-]+a[i][j];
    for(int i=;i<=n;i++)
        for(int j=;j<=n;j++)
            if(a[i][j])
            {
                int l=,r=min(min(i,j),min(n-i+,n-j+)),cnt=;
                while(l<=r)
                {
                    int mid=(l+r)>>;
                    if(dfs(i-mid+,j,i+mid-,j)==mid*-&&dfs(i,j-mid+,i,j+mid-)==mid*-&&dfs(i-mid+,j-mid+,i+mid-,j+mid-)==mid*-) l=mid+,cnt=mid;
                    else r=mid-;
                }
                ans=max(ans,cnt*-);
            }
    printf("%d",ans);
    return ;
}

T3 柱状图

题目

【题目描述】

在统计学中，柱状图是用来描述事件发生频率的一种图形语言，它是一种锯齿形的多边形，可以看做是一些长方形排列而成的。这些长方形的底边同为一个单位长度，但它们有不同的高度。对于给定的长方形，某些排列会使组成的多边形达到周长最长。你的任务是找出最长的周长以及构成最长周长的可能排列总数。

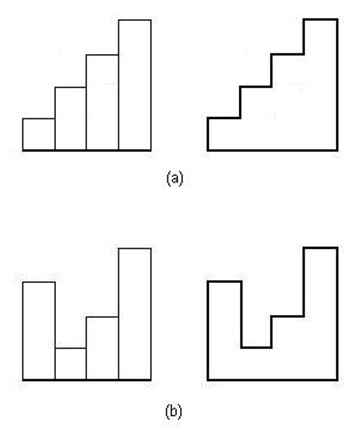
在图（a）中，组成多边形的长方形高度分别为{1，2，3，4}，它的周长为16个单位长度。在图（b）中，组成多边形的长方形高度分别为{3，1，2，4}，它的周长为20个单位长度。

【输入格式】

输入文件包含多组数据。

每组数据第一行为一个整数n (2≤n≤15)，描述有一共有多少个长方形。第二行为n个整数，表示n个长方形的高。

当n=0 时，表示输入数据结束。保证数据组数不超过16。

【输出格式】

对于每组数据，输出一个整数表示答案。

【输入样例】

【输出样例】

【数据规模】

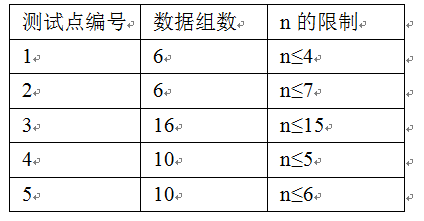
解析

不难发现，这题其实是全排列。

Code

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
inline int read()
{
    int num=,w=;
    char ch=getchar();
    while(ch<''||ch>'')
    {
        if(ch=='-') w=-;
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        num=(num<<)+(num<<)+ch-'';
        ch=getchar();
    }
    return num*w;
}
int n,a[],ans=,tot,f[];
long long sum;
int main()
{
    n=read(),f[]=;
    for(int i=;i<=;i++) f[i]=f[i-]*i;
    while(n)
    {
        tot=n*,ans=;
        for(int i=;i<=n;i++) a[i]=read(),tot+=a[i]*;
        sort(a+,a++n);
        if(n%==)
        {
            for(int i=;i<=(n-)/;i++) ans+=a[i]*;
            sum=f[n/+]*f[n/];
        }
        else
        {
            for(int i=;i<=n/-;i++) ans+=a[i]*;
            ans+=a[n/]*,sum=f[n/-]*f[n/]*n;
        }
        cout<<tot-ans<<" "<<sum<<endl;
        n=read();
    }
    return ;
}

T4 最长公共子序列

题目

【题目描述】

给定两个长度为5n的序列A,B。保证1~n这n个数在A,B中分别出现5次。求A,B最长公共子序列。

【输入格式】

第一行一个正整数n。

接下来两行，每行5n个正整数，表示序列A,B。

【输出格式】

输出一个整数，最长公共子序列的长度。

【输入样例】

【输出样例】

【数据规模】

对于30%的数据，n≤10。

对于60%的数据，n≤1000。

对于100%的数据，n≤20000。

解析

一下来自于出题人的题解。

注意1~n这n个数分别在A与B中出现5次。

枚举i，并维护f[j]表示A[1...i]和B[1...j]的最长公共子序列，且以B[j]为结尾。

对于每个x，用二维数组存下x在B中的所有位置，再枚举A[i]在B中的所有位置k。

此时，所有f[j]都是A[1...i-1]和B[1...j]的最长公共子序列。

令g[k]=max(f[1]~f[k-1])+1，即g[k]为A[1...i]和B[1...k]的最长公共子序列。

若B[j]!=A[i]，则g[j]=f[j]，即f[j]不改动。

所以只需做单点修改，并求前缀最大值，具体可以用树状数组维护f[j]的前缀最大值。

Code

#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <cstdio>
#include <vector>
#include <cmath>
using namespace std;
inline int read()
{
    int num=;
    char ch=getchar();
    while(ch<''||ch>'') ch=getchar();
    while(ch>=''&&ch<='')
    {
        num=(num<<)+(num<<)+ch-'';
        ch=getchar();
    }
    return num;
}
const int N=2e4+;
int n,a[N*],b[N*],c[N*],d[];
vector<int> g[N*];
void change(int x,int y)
{
    for(int i=x;i<=n*;i+=i&-i) c[i]=max(c[i],y);
}
int ask(int x)
{
    int ans=;
    for(int i=x;i;i-=i&-i) ans=max(ans,c[i]);
    return ans;
}
int main()
{
    n=read();
    for(int i=;i<=n*;i++) a[i]=read();
    for(int i=;i<=n*;i++) b[i]=read(),g[b[i]].push_back(i);
    for(int i=;i<=n*;i++)
    {
        for(int j=;j<=;j++)
        {
            int x=g[a[i]][j];
            d[j]=ask(x-);
        }
        for(int j=;j<=;j++)
        {
            int x=g[a[i]][j];
            change(x,d[j]+);
        }
    }
    cout<<ask(n*);
    return ;
}