PCA：主成分分析

PCA的概念：

主要思想是将n维特征映射到k维上，这k维是全新的正交特征，这k维特征被称为主成分，在原数据的基础上重新构造出来k维。就是从原始的空间顺序的找出一组相互正交的坐标轴，新坐标轴的选择和数据本身有很大的关系。其中，第一个坐标轴是从原数据中方差最大的方向，第二个新坐标轴选择是与第一个坐标轴正交平面中使得方差最大的，第三个轴是与第一二轴正交的平面中方差最大的，依次类推。依次类推，可以得到n个这样的坐标轴。通过这种方式获得的新的坐标轴，我们发现，大部分方差都包含在前面k个坐标轴中，后面的坐标轴所含的方差几乎为0。于是，我们可以忽略余下的坐标轴，只保留前面k个含有绝大部分方差的坐标轴。事实上，这相当于只保留包含绝大部分方差的维度特征，而忽略包含方差几乎为0的特征维度，实现对数据特征的降维处理。

PCA算法：

优点：降低数据的复杂性，识别最重要的多个特征

缺点：不一定需要，可能损失有用信息

适用数据类型：数值型数据

数据集下载链接：http://archive.ics.uci.edu/ml/machine-learning-databases/

在PCA中应用的数据集：http://archive.ics.uci.edu/ml/machine-learning-databases/secom/

（1）打开数据集计算特征数目：（列为特征数）在secom数据集中一行代表一条数据，将nan值改为非nan值的平均值

（2）去除特征值

（3）计算协方差矩阵，对该矩阵进行特征值分析。

将数据转换成n个主成分的伪码：

（1）去除平均值

（2）计算协方差矩阵

（3）计算协方差矩阵的特征值和特征向量

（4）将特征值从大到小排序

（5）保留最上面的n个特征向量

（6）将数据转换到上述n个特征向量构建的新空间中

note:

参考：https://zhuanlan.zhihu.com/p/37777074

样本均值：

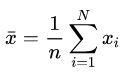
样本方差：

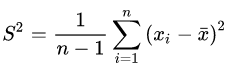
样本x和样本y的协方差：

样本均值，方差和协方差的区别：

样本均值：不同样本根据同一维求平均

方差是根据数据的同一维，针对n个样本计算得到的，

协方差：数据至少两维，表示样本（好多维）与样本之间的关系，协方差为正：样本x和样本y是正向关系，为负，是负向关系，等于0，说明x和y独立。

eg：对于3维数据（x,y,z）,协方差为：