【Luogu P2765】魔术球问题

Luogu P2765

一开始看到这道题完全想不到怎么做，绞尽脑汁也想不到怎么去构造这个网络流模型。

于是查看了多篇题解……学习了多篇题解的讲解，终于找到了思路。

本文参考了洛谷

这一道题的题意并不难理解，难就难在如何去构造模型。

显然有一个贪心策略，就是尽可能地放在已经放置过球的柱子上，尽可能少地使用尚未放置球的柱子。

把每一个球视为图上的一个节点，考虑把节点\(p\)拆成两个节点，使用\(p_1\)和\(p_2\)表示，分别令超级源点\(S\)与\(p_1\)、\(p_2\)与超级汇点\(T\)连接一条容量为1的边。

若球\(i,j(i<j)\)可以匹配，则令\(i_1\)与\(j_2\)之间连接一条容量为1的边。

容量为1的原因：每次只能在柱子最上方放球。

这个时候我们求一次最大流，只要最大流有变化，即产生了新的增广路，就可以认为这个球可以放置于原先已经放置过球的柱子上了。

如果最大流没有变化，那么说明这个球必须要新开一个柱子了。

我们只需要不断地重复这个过程，直到使用的柱子恰好大于\(n\)时，此时球的编号\(-1\)就是答案。

记录方案：在跑最大流时，记录当前点给出的流到了哪个点即可；新开柱子时记录一下第一个球的编号。

举个例子



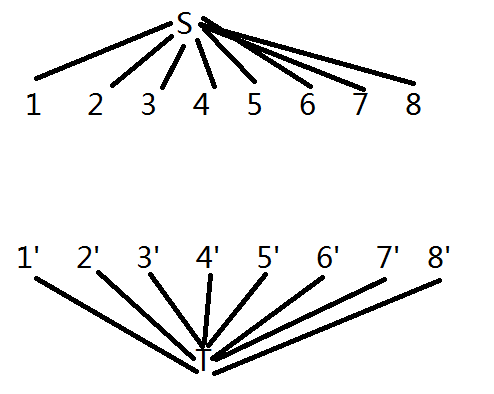
（为了方便分析已经画好了源点和汇点的所有边）

这是初始时刻的图。

当我们处理到\(3\)的时候，就可以在\(1\)和\(3'\)之间连接一条边。（为什么不在\(3,6\)连？因为\(3\)都没放哪来的\(6\)）



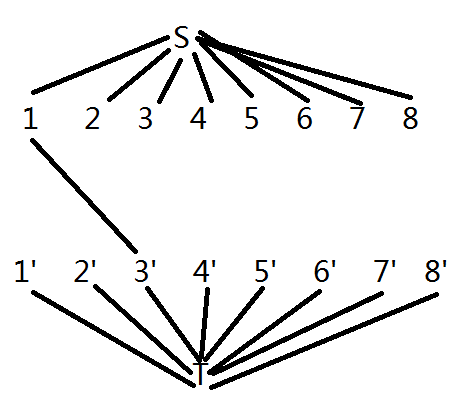
此时产生了一条增广路，也就是说\(3\)可以放置在\(1\)所在的那个柱子上。

接着不断重复即可。

值得注意的还有这样的情况：



注意红色这一条边。因为\(1,8\)能够匹配，所以可以连上这样一条边，但是这样并不意味着\(8\)可以放置在\(1\)上，因为\(1\)上方已经有\(3,6\)了。

所以，为了处理这样的情况，我们所有的边权都是\(1\)。

不过事实上这道题直接贪心就能过了

可这是网络流24题啊

#include<cstdio>
#include<algorithm>
#include<queue>
#include<cmath>
using namespace std;
struct data
{
    int next,to,val;
}e[50005];
int cnt=1,head[50005],cur[50005],dis[50005],rec[50005],ans[50005],n,ball;
void add(int u,int v,int w)
{
    e[++cnt].to=v;
    e[cnt].next=head[u];
    head[u]=cnt;
    e[cnt].val=w;
}
int bfs(int s,int t)
{
    queue<int> que;
    que.push(s);
    for (int i=1;i<=ball*2+1;i++) dis[i]=0,cur[i]=head[i];
    cur[t]=head[t];dis[t]=0;
    dis[s]=1;
    while (!que.empty())
    {
        int u=que.front();
        que.pop();
        for (int i=head[u];i;i=e[i].next)
        {
            int v=e[i].to;
            if (!dis[v]&&e[i].val>0)
            {
                dis[v]=dis[u]+1;
                if (v==t) return true;
                que.push(v);
            }
        }
    }
    return false;
}
int dfs(int u,int t,int flow)
{
    if (u==t||!flow) return flow;
    int used=0;
    for (int i=cur[u];i;i=e[i].next)
    {
        cur[u]=i;
        int v=e[i].to;
        if (dis[v]!=dis[u]+1) continue;
        int tmp=dfs(v,t,min(flow-used,e[i].val));
        if (!tmp) continue;
        used+=tmp;
        e[i].val-=tmp;
        e[i^1].val+=tmp;
        ans[u>>1]=v>>1;
        if (flow==used) return used;
    }
    return used;
}
bool Dinic(int s,int t)
{
    int tmp=0;
    while (bfs(s,t))
        tmp+=dfs(s,t,0x3f3f3f3f);
    return tmp;
}
int main()
{
    scanf("%d",&n);
    int now=0,s=1,t=50000;
    while (now<=n)
    {
        ball++;
        add(s,ball<<1,1),add(ball<<1,s,0);
        add(ball<<1|1,t,1),add(t,ball<<1|1,0);//拆点连边
        for (int i=sqrt(ball)+1;i*i<(ball<<1);i++) add((i*i-ball)<<1,ball<<1|1,1),add(ball<<1|1,(i*i-ball)<<1,0);
        //ball能够组成的完全平方数至少要比ball大1，但是必须小于ball的两倍
        if (!Dinic(s,t)))
        {
            now++;
            rec[now]=ball;
        }
    }
    printf("%d\n",ball-1);
    for (int i=1;i<now;i++)
    {
        for (int j=rec[i];j&&j!=(t>>1);j=ans[j])
            printf("%d ",j);
        printf("\n");
    }
    return 0;
}

参考资料：洛谷题解