1.前言

Apache Kylin™是一个开源的分布式分析引擎，提供Hadoop之上的SQL查询接口及多维分析（OLAP）能力以支持超大规模数据，最初由eBay Inc. 开发并贡献至开源社区。它能在亚秒内查询巨大的Hive表。

Kylin 核心：Kylin OLAP引擎基础框架，包括元数据（Metadata）引擎，查询引擎，Job引擎及存储引擎等，同时包括REST服务器以响应客户端请求
扩展：支持额外功能和特性的插件
整合：与调度系统，ETL，监控等生命周期管理系统的整合
用户界面：在Kylin核心之上扩展的第三方用户界面
驱动：ODBC 和 JDBC 驱动以支持不同的工具和产品，比如Tableau

2.操作步骤

2.1拷贝jar包到FR工程

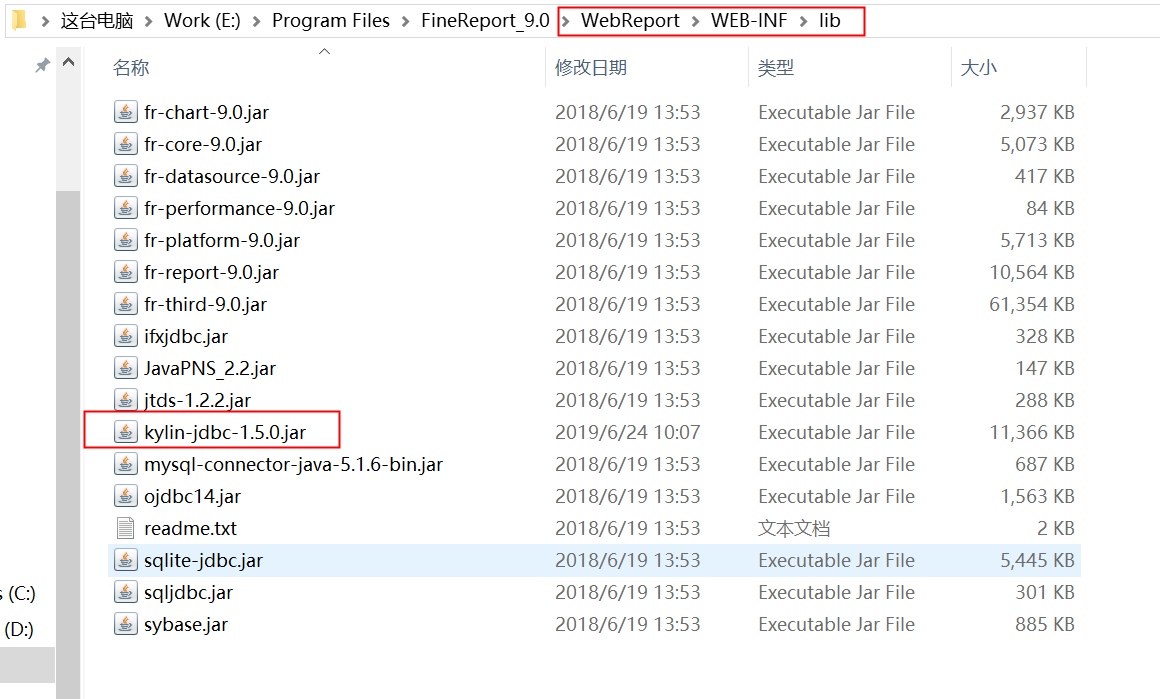
将APACHE KYLIN jdbc驱动包拷贝至报表工程%FR_HOME%/WebReport/WEB-INF/lib下，之后重启设计器。
注：若需要连接的是1.5版本以上的Apache Kylin，需下载1.5版本的APACHE KYLIN驱动包。

如下图：

2.2设计器中定义数据连接

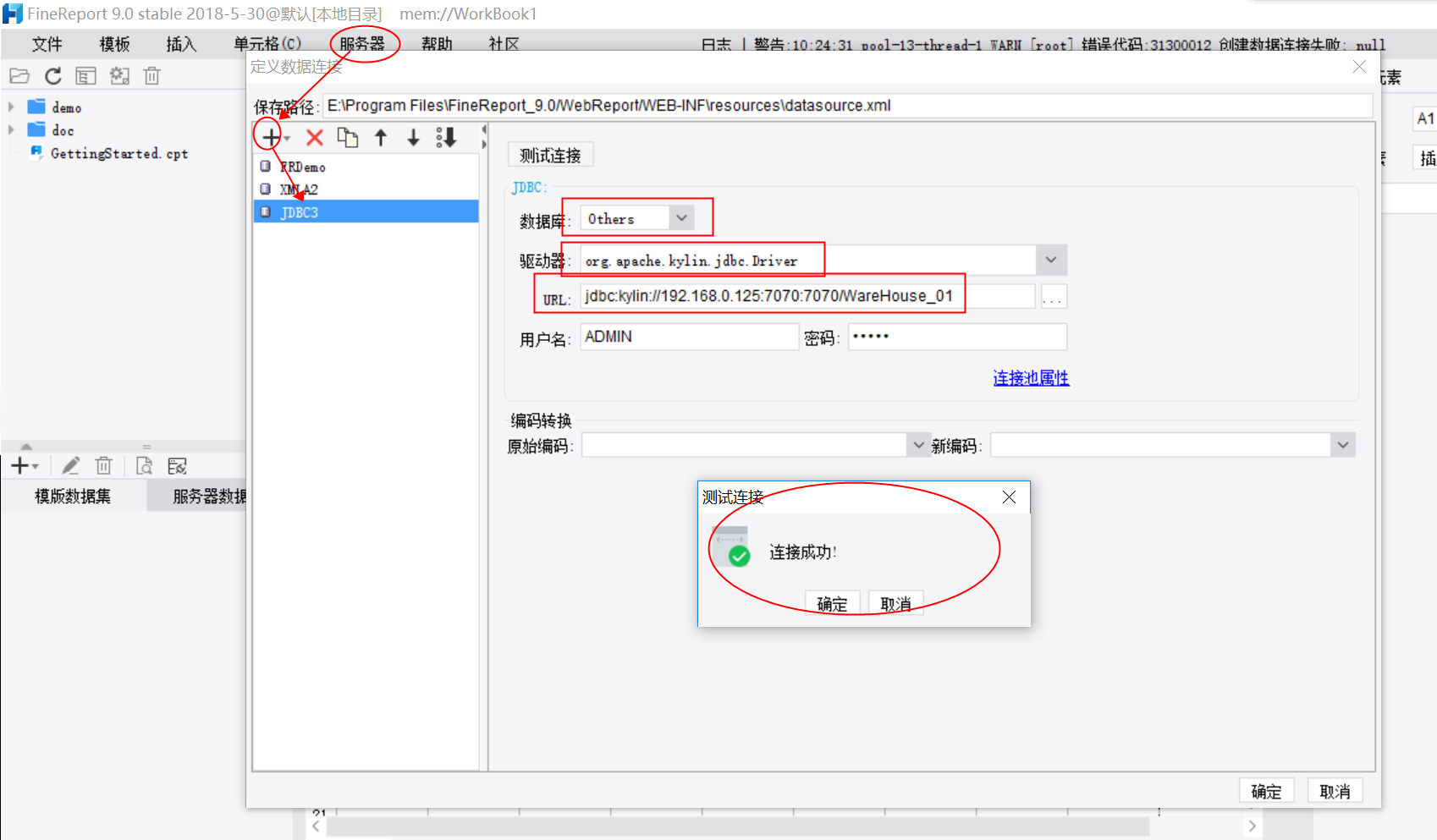
点击设计器服务器>定义数据连接，新建一个JDBC数据连接，数据库选择：Others，驱动器填写：org.apache.kylin.jdbc.Driver，URL填写：jdbc:kylin://localhost:7070/kylin_project_name，填写用户名、密码，测试连接按钮，连接成功即可。

参考：https://help.finereport.com/finereport9.0/doc-view-1613.html?tdsourcetag=s_pcqq_aiomsg

FineReport连接ApacheKylin的更多相关文章

  1. FineReport连接多维数据库示例及操作

    1. 描述 FineReport连接多维数据库,首先要通过数据连接将多维数据库与FineReport连接起来,然后在数据连接的基础上新建多维数据库XMLA数据集,用于模板设计. 2.XMLA数据连接 ...

  2. finereport连接mysql8.0的解决办法

    1.具体连接操作 首先将mysql-connector-java-8.0以上的jar包放到FindReport安装目录下的webapps下的WEB-INF下的lib下. 打开finereport,找到 ...

  3. FineReport连接SSAS多维数据库

    1.服务器——定义数据连接,如下图: 2.配置SSAS服务器地址及登录名密码: 注意这里的用户名.密码是指的服务器的登录名和登录密码,也就是你远程桌面的登录用户名和密码,不是数据库的登录用户名密码. ...

  4. FineReport如何用JDBC连接阿里云ADS数据库

    在使用FineReport连接阿里云的ADS(AnalyticDB)数据库,很多时候在测试连接时就失败了.此时,该如何连接ADS数据库呢? 我们只需要手动将连接ads数据库需要使用到的jar放置到%F ...

  5. 帆软报表FineReport中数据连接的JDBC连接池属性问题

    连接池原理 在帆软报表FineReport中,连接池主要由三部分组成:连接池的建立.连接池中连接使用的治理.连接池的关闭.下面就着重讨论这三部分及连接池的配置问题. 1. 连接池原理 连接池技术的核心 ...

  6. FineReport8.0如何连接FineIndex取数分析

    1. 描述 在3.7及之前版本,FineReport连接都是通过安装多维数据集插件,然后通过多维数据库的方式连接FineBI(3.4-3.6对应711,3.7对应8.0),从4.0版本开始,FineR ...

  7. 集团公司（嵌入ETL工具）财务报表系统解决方案

    集团公司(嵌入ETL工具)财务报表系统解决方案 一.项目背景: 某集团公司是一家拥有100多家子公司的大型集团公司,旗下子公司涉及各行各业,包括:金矿.铜矿.房产.化纤等.由于子公司在业务上的差异,子 ...

  8. 集团公司（嵌入ETL工具）財务报表系统解决方式

    集团公司(嵌入ETL工具)財务报表系统解决方式 一.项目背景: 某集团公司是一家拥有100多家子公司的大型集团公司,旗下子公司涉及各行各业,包含:金矿.铜矿.房产.化纤等.因为子公司在业务上的差异.子 ...

  9. FineReport如何连接和使用MongoDB数据库

    随着NoSQL数据库越来越流行,MongoDB数据库作为NoSQL数据库中的领头羊,使用也越来越广泛.为此,FineReport V8.0版本提供了数据连接和数据集接口,可以通过开发一款可以连接和使用 ...

随机推荐

  1. log4j配置每天生成一个日志文件

    首先需要配置web.xml里面: <servlet-name>log4j-init</servlet-name> <servlet-class>com.free.c ...

  2. Linux下使用cx_Oracle的一些配置

    在安装完成cx_Oracle后,import  cx_Oracle时报错,首先查看.bash_profile文件中环境变量配置 # .bash_profile # Get the aliases an ...

  3. linux 以导入文件形式添加定时任务（crontab）时需要注意的坑

    在实际操作过程中发现,使用导入文件形式添加定时任务时,会将用户已有的定时任务全部覆盖清理(先清空,再重新导入),所以在使用文件导入定时任务时,需要先将已有定时任务导出,然后将新任务进行追加到已有定时任 ...

  4. 11-C#笔记-函数-方法

    # 1 函数基本使用 函数的调用方法用C++. 主函数要在一个Class中,静态的,无返回值: 见示例 using System; namespace CalculatorApplication { ...

  5. MySQL 官方测试库

    MySQL 官方测试库 github 地址 https://github.com/datacharmer/test_db MySQL 文档地址 https://dev.mysql.com/doc/em ...

  6. CentOS7 开放端口 通过 firewall-cmd 工具来操作防火墙

    CentOS7 提供了 firewall-cmd 工具来操作防火墙. firewall-cmd --permanent:表示设置为持久,配置被写入配置文件,跨重启,不会立即生效,重新加载配置后生效.不 ...

  7. Java String语法

    String类代表字符串. Java程序中的所有字符串文字(例如"abc" )都被实现为此类的实例. 字符串不变; 它们的值在创建后不能被更改. 字符串缓冲区支持可变字符串. 因为 ...

  8. KDiff3使用指南

    http://kdiff3.sourceforge.net/ KDiff3 is a diff and merge program that compares or merges two or thr ...

  9. django ORM创建

    简短的例子 from django.db import models class Person(models.Model): first_name = models.CharField(max_len ...

  10. 【LG2605】[ZJOI2010]基站选址

    [LG2605][ZJOI2010]基站选址 题面 洛谷 题解 先考虑一下暴力怎么写,设\(f_{i,j}\)表示当前\(dp\)到\(i\),且强制选\(i\),目前共放置\(j\)个的方案数. 那 ...