过拟合产生的原因（Root of Overfitting）

之前在《过拟合和欠拟合（Over fitting & Under fitting）》一文中简要地介绍了过拟合现象，现在来详细地分析一下过拟合产生的原因以及相应的解决办法。

过拟合产生的原因：

第一个原因就是用于训练的数据量太少。这个很好理解，因为理想的训练数据是从所有数据中抽取的无偏差抽样。如果训练数据量较少，那么很有可能训练数据就不能完全反映所有数据的规律。因此模型很可能学习到的是一些特殊的例子，而不是真实的规律。

之前说过，过拟合就是模型把噪音也学习了进去。其中一个噪音就是大家所熟知的随机产生的噪音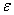（stochastic noise），比如说测量误差，记录误差等等，这也是第二个原因。

第三个原因是目标函数的复杂度很高，目标函数和假设函数之间的差距也可以看作是一种噪音，称为确定性噪音（deterministic noise）。在训练数据有限的情况下，如果目标函数很复杂，那么就算假设函数与之很接近，也会产生较大的噪音。

下图展现了在训练数据有限的情况下，目标函数和假设函数之间的差距。

• 左图：目标函数是一个十次多项式函数，根据目标函数产生了15个数据点，数据产生时加入了一些随机噪音，分别使用二次多项式（绿线）和十次多项式（红线）拟合
• 右图：目标函数是一个五十次多项式函数，根据目标函数产生了15个数据点，数据产生时不加入噪音，分别使用二次多项式（绿线）和十次多项式（红线）拟合

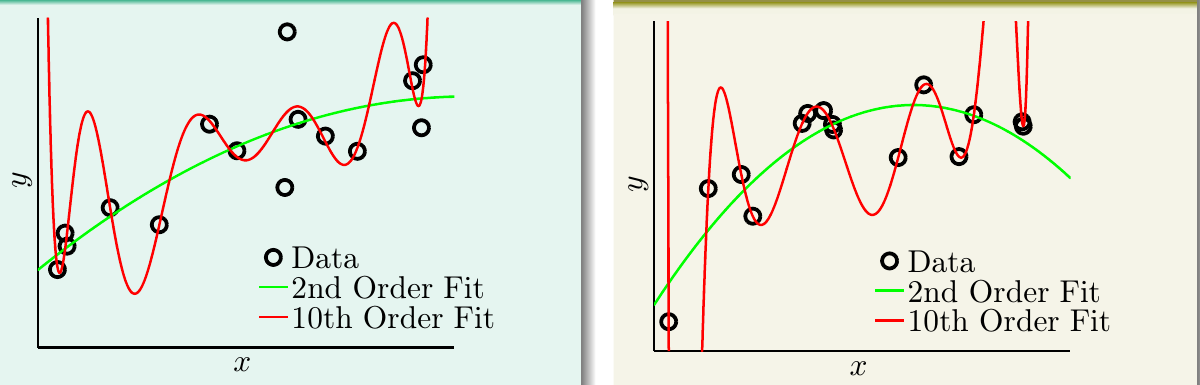
经过试验，这两个场景都是十次多项式的训练误差小，但是其验证误差要比二次多项式的大很多。这说明十次多项式发生了过拟合现象。

下图是用二次多项式和十次多项式拟合的学习曲线：

可以看出，十次多项式函数的训练误差一直要比二次多项式函数的低，但是当训练数据有限时，十次多项式函数的验证误差要比二次多项式函数的高不少。

一般我们会认为假设函数离目标函数越接近越好，但是显然，在训练数据有限的情况下，这种想法是不正确的。因此，当训练数据有限时，应该用简单的模型来拟合，这样还有可能会取得不错的效果。之前是不是常听到别人说线性回归模型虽然很简单，但是往往会取得不错的预测效果？这也正说明了这个道理。

下图是当目标函数复杂度固定时，样本量与噪音强度对过拟合程度的影响（深红色表示过拟合程度很高）：

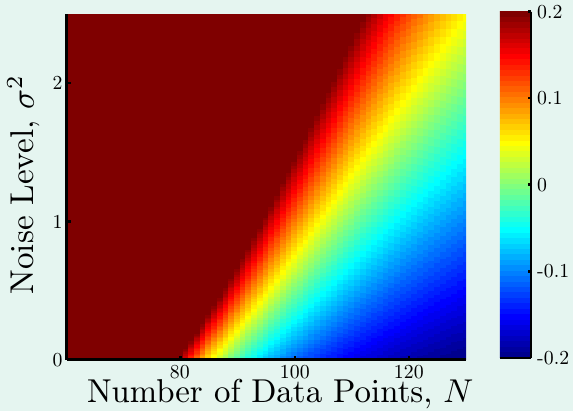
可以看出，样本量越少，噪音强度越高，过拟合程度也就越高。

下图是当噪音强度固定时，样本量与目标函数复杂度对过拟合程度的影响（深红色表示过拟合程度很高）：

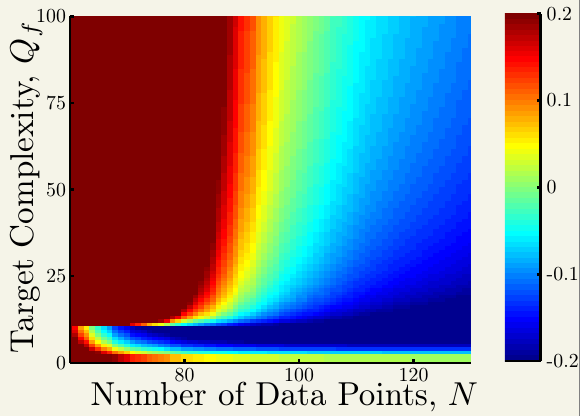
可以看出，样本量越少，目标函数复杂度越高，过拟合程度也就越高。

这两张图的区别在于左下角，可以看到，第二张图，当样本量很少，目标函数复杂度很低时，也会产生过拟合现象。这是因为使用了过于复杂的模型来拟合数据，这也带出了第四个原因---模型复杂度比目标函数高。

总结一下过拟合产生的原因：

• 训练数据太少
• 数据噪音强度大：随机噪音（stochastic noise），确定性噪音（deterministic noise）
• 模型复杂度太高

解决办法：

• 增加训练数据量 --- 一般情况下，由于经济条件的限制，我们没有办法获得更多的训练数据。如果没有办法获得更多的训练数据，那么可以对已有的样本进行简单的变换，从而获得更多的样本。比如识别手写数字时，可以把数字稍作倾斜，又或者识别图像时，可以对图像做翻转，这样特征发生改变，但是目标保持不变，这样就可以当成产生一些新的样本，称为虚拟样本。但是需要注意，这种方法产生的数据不一定符合原有数据的分布，因此新构建的虚拟样本要尽量合理。
• 减少随机噪音 --- 可以清洗数据（比如：修正不准确的点，删除不准确的点，等），但是如果这些点相比训练数据很少的话，这种处理产生的效果不太明显。
• 减少确定性噪音，降低模型复杂度 --- 使用简单的模型拟合数据；对现有模型进行正则化。