6-19 Count Connected Components（20 分）

Write a function to count the number of connected components in a given graph.

Format of functions:

int CountConnectedComponents( LGraph Graph );

where LGraph is defined as the following:

typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode{
    Vertex AdjV;
    PtrToAdjVNode Next;
};

typedef struct Vnode{
    PtrToAdjVNode FirstEdge;
} AdjList[MaxVertexNum];

typedef struct GNode *PtrToGNode;
struct GNode{
    int Nv;
    int Ne;
    AdjList G;
};
typedef PtrToGNode LGraph;

The function CountConnectedComponents is supposed to return the number of connected components in the undirected Graph.

Sample program of judge:

#include <stdio.h>
#include <stdlib.h>

typedef enum {false, true} bool;
#define MaxVertexNum 10  /* maximum number of vertices */
typedef int Vertex;      /* vertices are numbered from 0 to MaxVertexNum-1 */

typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode{
    Vertex AdjV;
    PtrToAdjVNode Next;
};

typedef struct Vnode{
    PtrToAdjVNode FirstEdge;
} AdjList[MaxVertexNum];

typedef struct GNode *PtrToGNode;
struct GNode{
    int Nv;
    int Ne;
    AdjList G;
};
typedef PtrToGNode LGraph;

LGraph ReadG(); /* details omitted */

int CountConnectedComponents( LGraph Graph );

int main()
{
    LGraph G = ReadG();
    printf("%d\n", CountConnectedComponents(G));

    return 0;
}

/* Your function will be put here */

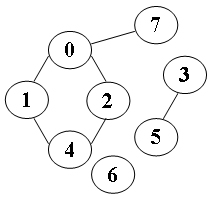
Sample Input (for the graph shown in the figure):

8 6
0 7
0 1
2 0
4 1
2 4
3 5

Sample Output:

3


找图的连通分支

代码：

int CountConnectedComponents( LGraph Graph )
{
    int vis[MaxVertexNum] = {};
    int c = ;
    for(int i = ;i < Graph -> Nv;i ++)
    {
        if(vis[i] == )
        {
            c ++;
            vis[i] = ;
            PtrToAdjVNode t;
            int head = ,tail = ;
            int s[];
            s[tail ++] = i;
            while(head < tail)
            {
                t = Graph -> G[s[head]].FirstEdge;
                while(t)
                {
                    if(!vis[t->AdjV])
                    {
                        vis[t->AdjV] = ;
                        s[tail ++] = t -> AdjV;
                    }
                    t = t -> Next;
                }
                head ++;
            }
        }
    }
    return c;
}