数据结构（三）--- B树（B-Tree）

   文章图片代码来自邓俊辉老师的课件

概述

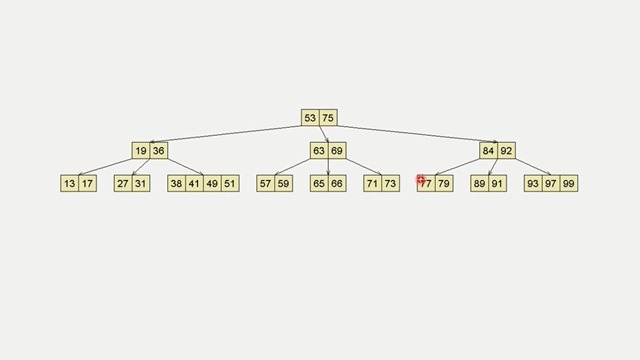
上图就是 B-Tree 的结构，可以看到这棵树和二叉树有点不同---“又矮又肥”。同时子节点可以有若干个小的子节点构成。那么这样一棵树又有什么作用呢？

动机

我们知道电脑的访问内存比访问外的存I/O操作快了，但是内存的容量大小又只有那么一点点（相对于外存），所以计算机访问的过程常常使用高速缓存。使用高速缓存也是在以下两个事实想出的策略。

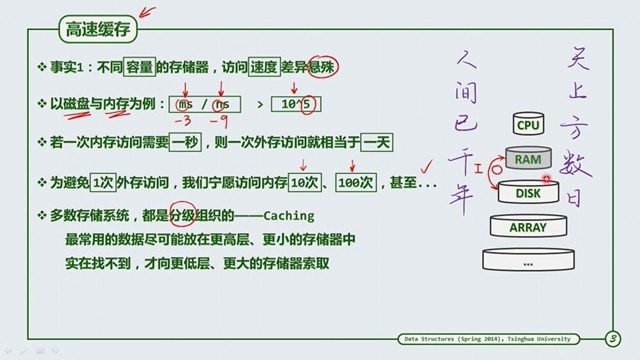
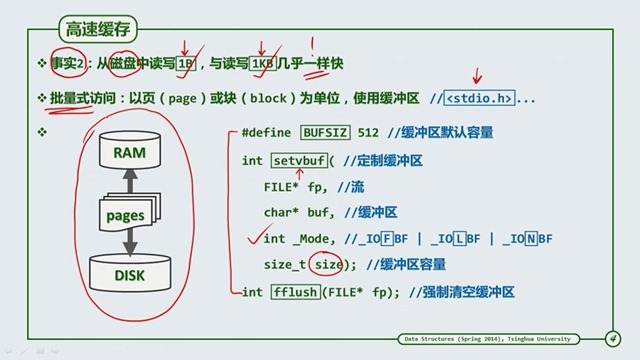
而B-Tree这种结构就是根据这种情况被发掘出来的。下图 m 指的是每次的数据块数量

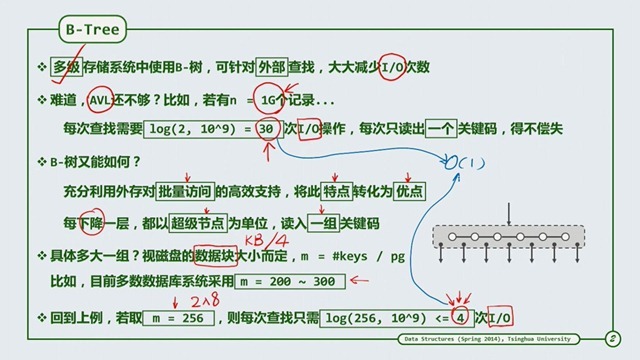
B-Tree 介绍

多路平衡

关键码指的是一个超级节点包含的子节点。

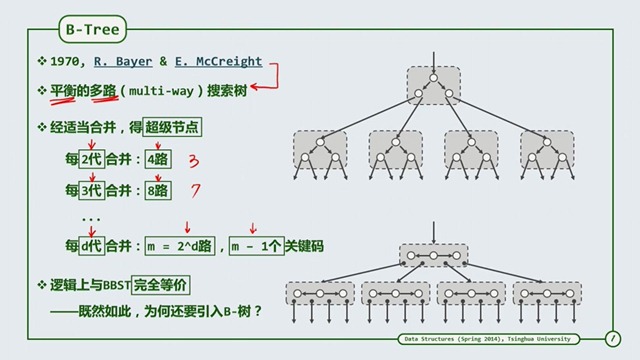
B-Tree定义

m阶指的是m路，一个超级节点最大可以分出多少路。二叉树分出两边，左边和右边，就是两路，二阶。

下面是几个定义为不同阶的B-树。

分支数

B-Tree的分支数有个上下限，例如6阶的B-Tree（m=6），又被称为 “(3,6)-树”，类似的还有 “(3,5)-树”，“(2,4)-树”，而(2,4)树就是我们后面要学的红黑树。

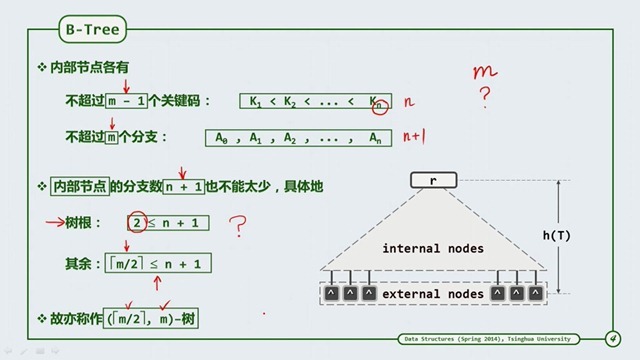
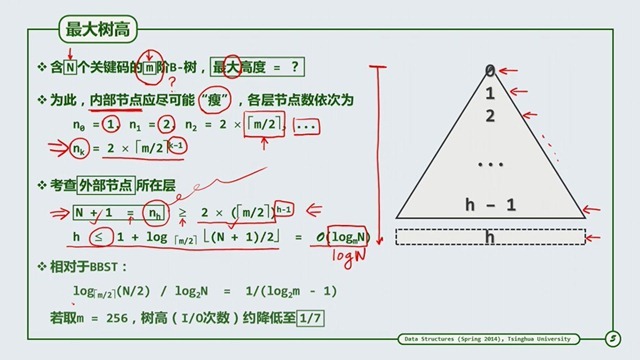
最大树高和最小数高

可以看到对于“含N个关键码的m阶B-树”的最大树高和最小树高之间的波动并不大。

代码实现

代码实现主要的两个方法为插入和删除。其中插入的时候需要注意查看某个节点是否超出了阶数，若超出了，需要分裂，最坏的情况就是分裂到根部，而删除操作需要注意查看是否会产生下溢，处理下溢，我们常用的方法就是旋转和合并。

插入

下图分别是分裂和再分裂的图示。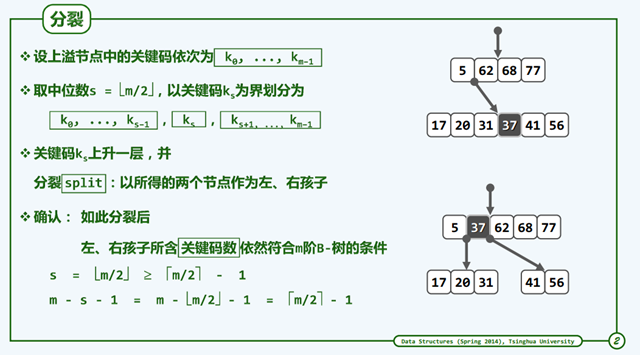    

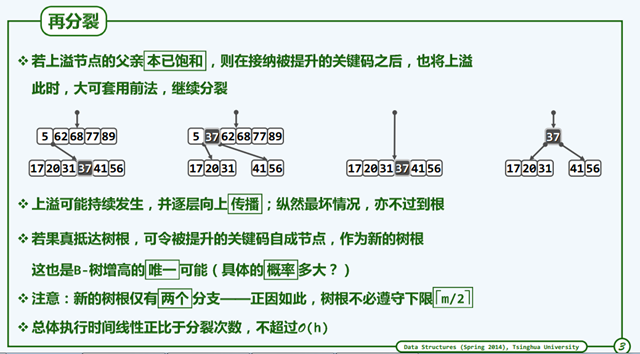
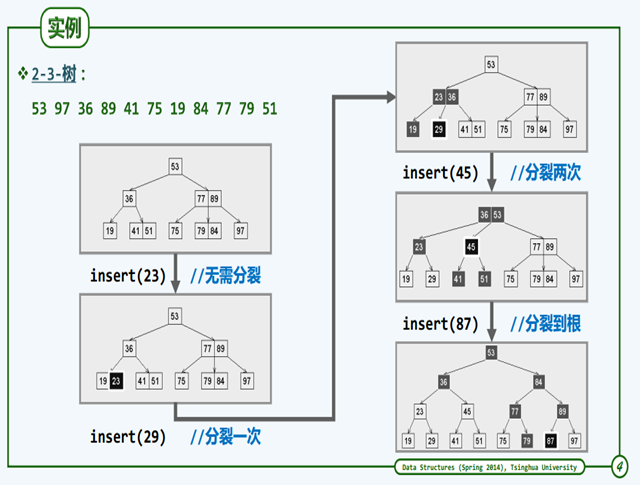
删除

删除操作的旋转和合并。

旋转可以理解为左右兄弟有足够的节点，向左右兄弟节点借来补充的操作。

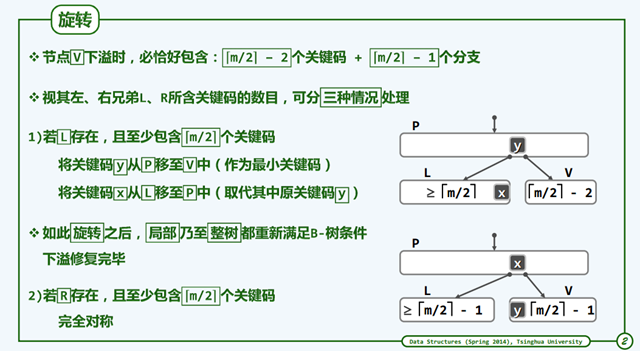
假如向兄弟们借都不成功，那就拿父节点的一个元素一起合并，代码实现中有分左合并和右合并。

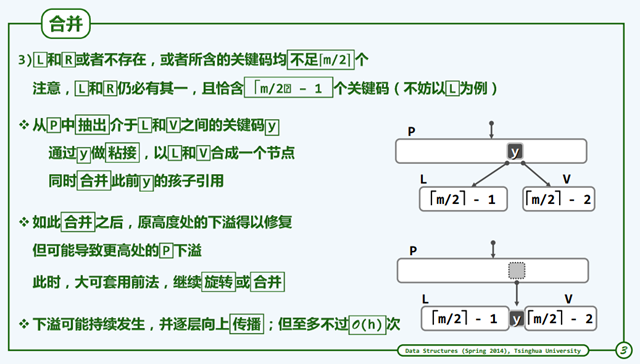
java版本代码

B-树节点类

package BTree;

import java.util.Vector;

/**
 * B-树的节点Bean
 * 包含一个有序向量 value 和 指向子节点的 child 向量
 *
 */
public class BTreeNode {
    BTreeNode parent;
    Vector<BTreeNode> child;
    Vector<Integer> value;

    public BTreeNode(int value, BTreeNode left, BTreeNode right) {
        if (this.value == null) {
            this.value = new Vector<>();
            this.value.sort(new VectorComparable());
        }
        if (child == null) {
            child = new Vector<>();
        }
        this.value.add(value);
        this.child.add(0, left);
        this.child.add(1, right);
        if (left != null) {
            left.parent = this;
        }
        if (right != null) {
            right.parent = this;
        }
    }

    public BTreeNode() {
        parent = null;
        if (this.value == null) {
            this.value = new Vector<>();
            this.value.sort(new VectorComparable());
        }
        if (child == null) {
            child = new Vector<>();
        }
    }

    /**
     * 一个关键块内的查找 查找到与否都返回一个index
     * 返回最靠近的值的原因是为了下面的节点继续查找
     *
     * @param value 查找的值
     * @return 不存在的情况返回最靠近的index 值 ， -1
     */
    public int search(int value) {
        int hot = -1;
        for (int i = 0; i < this.value.size(); i++) {
            if (this.value.get(i) > value) {
                return hot;
            } else if (this.value.get(i) < value) {
                hot = i;
            } else { // 相等
                return i;
            }
        }
        return this.value.size() - 1;
    }

    public int getIndexInValue(int compare) {
        for (int i = 0; i < this.value.size(); i++) {
            if (compare == value.get(i)) {
                return i;
            }
        }
        return -1;
    }

    /**
     * 查找当前node在父节点中的index
     *
     * @return -1 为父类不存在或是父类为null ，其他为当前节点在父节点为位置
     */
    public int getIndexFromParent() {
        if (parent == null) {
            return -1;
        }
        for (int i = 0; i < parent.child.size(); i++) {
            if (parent.child.get(i) == this) {
                return i;
            }
        }
        return -1;
    }

    public void addValue(int index, int val) {
        value.add(index, val);
        value.sort(new VectorComparable());
    }

    public void addValue(int val) {
        value.add(val);
        value.sort(new VectorComparable());
    }

}

B-树数据结构方法。

package BTree;

public class BTree {
    private BTreeNode root;
    private int degree; // m阶B-树 ，阶树至少为3

    /*
     * 私有方法
     */

    /**
     * 查找在哪个BTreeNode ,假如到了外部节点，返回该外部节点 返回的结果只有两种 ：
     * - 存在，返回该节点
     * - 不存在，返回值应该插入的节点
     *
     * @param val 查找的值
     * @return 返回搜索结果，假如该关键块不存在（到达了外部节点）就返回该关键快
     */
    private BTreeNode searchSurroundNode(int val) {
        BTreeNode node, hot = null;
        int rank;
        node = root;
        while (node != null) {
            rank = node.search(val);
            if (rank != -1 && node.value.get(rank) == val) { // 找到对应的值
                return node;
            } else {
                hot = node;
                if (node.child.get(rank + 1) == null) {
                    return hot;
                }
                node = node.child.get(rank + 1);
            }
        }
        // 到了外部节点
        return hot;
    }

    private void addNodeForBtNode(BTreeNode node, int rank, int val) {
        node.addValue(val);
        if (rank != -1) {
            node.child.add(rank + 2, null);
        } else {
            node.child.add(0, null);
        }
    }

    /*
     *  下面为可调用的方法
     */

    public BTree(int degree) {
        this.degree = degree;
    }

    /**
     * 返回值所在的节点
     *
     * @param val 插入的值
     * @return 找到的话返回节点，找不到返回 null
     */
    public BTreeNode search(int val) {
        BTreeNode node = searchSurroundNode(val);
        if (node.value.get(node.search(val)) == val) { // 该节点存在该值
            return node;
        }
        return null;
    }

    /**
     *
     * 插入的值都会进入到底部节点
     * @param val 插入的值
     * @return 是否插入成功
     */
    public boolean insert(int val) {
        if (root == null) {
            root = new BTreeNode(val, null, null);
            return true;
        }
        //root 已经创建，插入的值最终会到达底部，然后插进去
        BTreeNode node = searchSurroundNode(val);
        int rank = node.search(val);
        if (rank != -1 && node.value.get(rank) == val) { // 该节点存在该值,返回插入失败
            return false;
        } else { // 值将会插入该关键码
            addNodeForBtNode(node, rank, val);
            split(node);
            return true;
        }
    }

    private void split(BTreeNode node) {
        while (node.value.size() >= degree) {
            // 1.取中数
            int midIndex = node.value.size() / 2;
            BTreeNode rightNode = new BTreeNode();
            for (int i = midIndex + 1; i < node.value.size(); i++) {
                rightNode.addValue(node.value.remove(i));
                if (i == midIndex + 1) {
                    rightNode.child.add(node.child.remove(i));
                }
                rightNode.child.add(node.child.remove(i));
            }
            for (BTreeNode rn : rightNode.child) {
                if (rn != null) {
                    rn.parent = rightNode;
                }
            }

            // 移除原节点记得移除对应它的子节点
            int insertValue = node.value.remove(midIndex);
            if (node.parent != null) { // 存在父节点,把分裂点添加在父节点上
                node.parent.addValue(insertValue);
                /*
                 * 对插入的节点的子节点进行处理
                 * 1.得出插入点的index
                 * 2.左边子节点连接原node，右节点连接 rightNode
                 */
                int indexInValue = node.parent.getIndexInValue(insertValue);
                node.parent.child.add(indexInValue + 1, rightNode);
                rightNode.parent = node.parent;
                node = node.parent;
            } else { // 不存在父节点，并且当前节点溢出
                root = new BTreeNode(insertValue, node, rightNode);
                break;
            }
        }
    }

    public boolean delete(int val) {
        //node 为要删除的val所在的节点
        BTreeNode node = search(val);
        if (node != null) {
            int rank = node.getIndexInValue(val);
            // 找到继承结点并代替
            if (node.child.get(0) != null) { //非底部节点
                BTreeNode bottom = node.child.get(rank + 1);
                while (bottom.child.get(0) != null) {
                    bottom = bottom.child.get(0);
                }
                node.value.set(rank, bottom.value.get(0));
                bottom.value.set(0, val);
                node = bottom;
                rank = 0;
            }
            // 此时 node 一定是外部节点了（最底层）
            node.value.remove(rank);
            node.child.remove(rank + 1);
            // 由于删除了某个值，所以需要从兄弟中借一个来拼凑（旋转）
            // 当兄弟自己已到达下限，与父类合并成更大的节点，原来父节点所在的节点有可能-1后
            // 导致又达到了下限，然后循环
            solveUnderflow(node);
            return true;
        }
        return false;
    }

    /**
     * 下溢的节点 ：
     * - 外部节点
     * - 非外部节点
     *
     * @param node 下溢的节点
     */
    public void solveUnderflow(BTreeNode node) {
        //没有达到下溢的条件
        int condition = (degree + 1) / 2;
        if (node.child.size() >= condition) {
            return;
        }
        BTreeNode parent = node.parent;
        if (parent == null) { //到了根节点
            if (node.value.size() == 0 && node.child.get(0) != null) {
                root = node.child.get(0);
                root.parent = null;
                node.child.set(0, null);
            }
            return;
        }
        int rank = node.getIndexFromParent();

        //旋转
        if (rank > 0 && parent.child.get(rank - 1).child.size() > condition) { //左旋转，从左兄弟拿一个
            BTreeNode ls = parent.child.get(rank - 1);
            node.addValue(0, parent.value.remove(rank - 1));
            parent.addValue(rank - 1, ls.value.remove(ls.value.size() - 1));
            /*
             *   被取走的节点可能存在子节点，需要放在新的位置
             *   有可能上一次进行合并操作中，父节点的关键码为空了，
             *   但是父节点还存在子节点（不为null）
             */
            node.child.add(0, ls.child.remove(ls.child.size() - 1));
            if (node.child.get(0) != null) {
                node.child.get(0).parent = node;
            }
            return;
        } else if (rank < parent.child.size() - 1 && parent.child.get(rank + 1).child.size() > condition) {  //右旋转，从右兄弟拿一个
            BTreeNode rs = parent.child.get(rank + 1);
            node.addValue(parent.value.remove(rank));
            parent.addValue(rs.value.remove(0));

            node.child.add(node.child.size(), rs.child.remove(0));
            if (node.child.lastElement() != null) {
                node.child.lastElement().parent = node;
            }
            return;
        }

        // 合并
        if (rank > 0) { // 左合并
            BTreeNode ls = parent.child.get(rank - 1);
            //父类节点转入到左节点
            ls.addValue(ls.value.size(), parent.value.remove(rank - 1));
            parent.child.remove(rank);
            //当前节点转入到左节点
            ls.child.add(ls.child.size(), node.child.remove(0));
            if (ls.child.get(ls.child.size() - 1) != null) {
                ls.child.get(ls.child.size() - 1).parent = ls;
            }
            // 当前节点有可能value为空，但是child不为空。
            // value 为空不移动，不为空移动
            while (node.value.size() != 0) {
                ls.addValue(node.value.remove(0));
                ls.child.add(ls.child.size(), node.child.remove(0));
                if (ls.child.get(ls.child.size() - 1) != null) {
                    ls.child.get(ls.child.size() - 1).parent = ls;
                }
            }

        } else {   //右合并,有可能 rank = 0
            BTreeNode rs = parent.child.get(rank + 1);
            //父类节点转入到右节点
            rs.addValue(0, parent.value.remove(rank));
            //父类节点断开与当前节点的连接
            parent.child.remove(rank);
            //当前节点转入到右节点
            rs.child.add(0, node.child.remove(0));
            if (rs.child.get(0) != null) {
                rs.child.get(0).parent = rs;
            }
            while (node.value.size() != 0) {
                rs.addValue(0, node.value.remove(0));
                rs.child.add(0, node.child.remove(0));
                if (rs.child.get(0) != null) {
                    rs.child.get(0).parent = rs;
                }
            }

        }
        solveUnderflow(parent);
    }

    public int height() {
        int h = 1;
        BTreeNode node = root;
        while (node != null) {
            if (node.child.get(0) != null) {
                h++;
                node = node.child.get(0);
            } else {
                break;
            }
        }
        return h;
    }

}

最后是一个测试的方法。

package BTree;

public class BTreeTest {
    public static void main(String[] args) {
        BTree tree = new BTree(3);
        tree.insert(53);
        tree.insert(97);
        tree.insert(36);
        tree.insert(89);
        tree.insert(41);
        tree.insert(75);
        tree.insert(19);
        tree.insert(84);
        tree.insert(77);
        tree.insert(79);
        tree.insert(51);
//        System.out.println(tree.height());
//        tree.insert(23);
//        tree.insert(29);
//        tree.insert(45);
//        tree.insert(87);
//        System.out.println("-------------");
        System.out.println("插入节点以后的树的高度 ： "+tree.height());
        System.out.println("-------------");
//        tree.delete(41);
//        tree.delete(75);
//        tree.delete(84);
//        tree.delete(51);

        tree.delete(36);
        tree.delete(41);
        System.out.println("删除节点以后的树的高度 ： "+tree.height());

    }
}

参考资料

• 邓俊辉老师的数据结构课程