【JUC源码解析】ConcurrentHashMap
简介
支持并发的哈希表。其中包括红黑树,扩容,分槽计数等知识点。
源码分析
常量
private static final int MAXIMUM_CAPACITY = 1 << 30; // 最大容量
private static final int DEFAULT_CAPACITY = 16; // 默认容量,2^n
static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8; // 可能的最大数组大小
private static final int DEFAULT_CONCURRENCY_LEVEL = 16; // 默认并发级别
private static final float LOAD_FACTOR = 0.75f; // 负载因子
static final int TREEIFY_THRESHOLD = 8; // 链表转树阈值,链表长度超过8时转成红黑树
static final int UNTREEIFY_THRESHOLD = 6; // 树转链表阈值,树的元素小于等于6时转成链表
static final int MIN_TREEIFY_CAPACITY = 64; // 最小转树容量
private static final int MIN_TRANSFER_STRIDE = 16; // 最小转换步长
private static int RESIZE_STAMP_BITS = 16; // 调整大小标记比特数
private static final int MAX_RESIZERS = (1 << (32 - RESIZE_STAMP_BITS)) - 1; // 最大的可以调整大小的线程数
private static final int RESIZE_STAMP_SHIFT = 32 - RESIZE_STAMP_BITS; // 调整大小的标记移位 static final int MOVED = -1; // 转移结点hash值
static final int TREEBIN = -2; // 树根结点hash值
static final int RESERVED = -3; // 保留hash
static final int HASH_BITS = 0x7fffffff; // 正常结点hash的有效位 static final int NCPU = Runtime.getRuntime().availableProcessors(); // CPU的个数
属性
transient volatile Node<K, V>[] table; // hash表,第一次插入数据时初始化,大小为2^n
private transient volatile Node<K, V>[] nextTable; // 扩容后的数组
private transient volatile long baseCount; // 基本大小
private transient volatile int sizeCtl; // 0:默认,-1:table正在初始化,-N:表示有N-1个线程正在进行扩容操作,此描述不准确,须结合resizeStamp推断;其他:1.未初始化,表示初始化大小;2.已经初始化,表示table的容量,默认为table大小的0.75倍,0.75n = 3n/4 = (1 - 1/4)n = n - n/4 = (n - (n >>> 2))
private transient volatile int transferIndex; // 转换索引,扩容时,下一个表索引
private transient volatile int cellsBusy; // 自旋锁(通过CAS锁定)
private transient volatile CounterCell[] counterCells; // 大小为2^n
构造方法
public ConcurrentHashMap() { // 无参构造
}
public ConcurrentHashMap(int initialCapacity) { // 构造方法
if (initialCapacity < 0) // 参数校验
throw new IllegalArgumentException();
// cap乘以负载因子loadFactor应该大于等于initialCapcity,即是,cap >= initialCapcity /
// loadFactor,这里是loadFactor = 0.75
// 即是,cap >= initialCapcity * 4/3 = initialCapcity + (1/3) *
// initialCapcity
// 构造方法里,是根据initialCapacity + (initialCapacity >>> 1) + 1确立的cap,
// initialCapacity >>> 1 = initialCapacity * (1/2) > initialCapacity *
// (1/3)满足要求
// 后面还有+1,应该是避免为0吧,毕竟要有元素
// 最后代入到tableSizeFor(int)方法里,使得最后的cap为2的n次方,如果输入的是10,最后的结果是16,大于且最贴近输入值
int cap = ((initialCapacity >= (MAXIMUM_CAPACITY >>> 1)) ? MAXIMUM_CAPACITY
: tableSizeFor(initialCapacity + (initialCapacity >>> 1) + 1));
this.sizeCtl = cap;
}
public ConcurrentHashMap(Map<? extends K, ? extends V> m) { // 构造方法
this.sizeCtl = DEFAULT_CAPACITY;
putAll(m);
}
public ConcurrentHashMap(int initialCapacity, float loadFactor) { // 构造方法
this(initialCapacity, loadFactor, 1);
}
public ConcurrentHashMap(int initialCapacity, float loadFactor, int concurrencyLevel) { // 构造方法
if (!(loadFactor > 0.0f) || initialCapacity < 0 || concurrencyLevel <= 0) // 参数校验
throw new IllegalArgumentException();
if (initialCapacity < concurrencyLevel)
initialCapacity = concurrencyLevel; // 不小于并发级别
long size = (long) (1.0 + (long) initialCapacity / loadFactor); // 同上
int cap = (size >= (long) MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : tableSizeFor((int) size);
this.sizeCtl = cap;
}
数据结构
Node
继承关系
static class Node<K, V> implements Map.Entry<K, V> {}
属性
final int hash; // hash值
final K key; // 键
volatile V val; // 值
volatile Node<K, V> next; // 指向下一个结点
构造方法
Node(int hash, K key, V val, Node<K, V> next) { // 构造方法
this.hash = hash;
this.key = key;
this.val = val;
this.next = next;
}
find方法
Node<K, V> find(int h, Object k) { // 根据hash值和键查找结点
Node<K, V> e = this; // 指向当前结点
if (k != null) { // 键不为空
do {
K ek;
if (e.hash == h && ((ek = e.key) == k || (ek != null && k.equals(ek)))) // hash值不同,直接比较下一个结点;否则,比较其地址或内容是否相等
return e;
} while ((e = e.next) != null);
}
return null;
}
TreeNode
继承关系
static final class TreeNode<K, V> extends Node<K, V> {
属性
TreeNode<K, V> parent; // 父结点
TreeNode<K, V> left; // 左子结点
TreeNode<K, V> right; // 又子结点
TreeNode<K, V> prev; // 前一个结点
boolean red; // 是否为红色结点
构造方法
TreeNode(int hash, K key, V val, Node<K, V> next, TreeNode<K, V> parent) { // 构造方法
super(hash, key, val, next);
this.parent = parent;
}
find方法
Node<K, V> find(int h, Object k) { // 查找
return findTreeNode(h, k, null);
}
findTreeNode方法
final TreeNode<K, V> findTreeNode(int h, Object k, Class<?> kc) { // 查找结点
if (k != null) { // k若为空,直接返回null
TreeNode<K, V> p = this; // 当前结点
do {
int ph, dir; // p的hash值,k与p的key的compare值
K pk; // p的key
TreeNode<K, V> q;
TreeNode<K, V> pl = p.left, pr = p.right; // p的左子结点,p的右子结点
if ((ph = p.hash) > h) // 如果当前结点的hash值大于h,说明目标结点在左子树
p = pl; // 令p指向左子结点
else if (ph < h) // 如果当前结点的hash值小于h,说明目标结点在右子树
p = pr; // 令p指向右子结点
else if ((pk = p.key) == k || (pk != null && k.equals(pk))) // 如果当前结点就是目标结点
return p; // 直接返回
else if (pl == null) // 如果ph ==
// h,但是当前结点不是目标结点,则查看左子结点是否存在,不存在则指向右子结点
p = pr;
else if (pr == null) // 如果左子结点存在,那么查看右子结点是否存在,不存在则指向左子结点
p = pl;
else if ((kc != null || (kc = comparableClassFor(k)) != null) // 如果左右子结点都存在,并且k的Class不为空,则比较k的值顺序
&& (dir = compareComparables(kc, k, pk)) != 0)
p = (dir < 0) ? pl : pr; // 目标结点小于当前结点,则指向左子结点,否则指向右子结点
else if ((q = pr.findTreeNode(h, k, kc)) != null) // 如果以上条件不满足,则递归查找右子树
return q; // 找到则返回
else // 最后,如果以上条件均不满足,由于已经递归查找了右子树,所以,p指向左子结点,循环查找
p = pl;
} while (p != null);
}
return null;
}
}
TreeBin
继承关系
static final class TreeBin<K, V> extends Node<K, V>{}
属性
TreeNode<K, V> root; // 红黑树根节点
volatile TreeNode<K, V> first; // 链表头结点
volatile Thread waiter; // 等待线程
volatile int lockState; // 锁状态
static final int WRITER = 1; // 001, 持有写锁
static final int WAITER = 2; // 010, 等待写锁
static final int READER = 4; // 100, 每获取读锁,增加此值
构造方法
TreeBin(TreeNode<K, V> b) { // 继承Node, 链表转红黑树
super(TREEBIN, null, null, null); // 调用父类的构造方法
this.first = b; // 头结点引用指向给定结点
TreeNode<K, V> r = null;
for (TreeNode<K, V> x = b, next; x != null; x = next) { // 从头结点开始往后遍历
next = (TreeNode<K, V>) x.next; // 指向下一个结点
x.left = x.right = null;
if (r == null) { // 根结点
x.parent = null; // 根节点没有父节点
x.red = false; // 红黑树根结点是黑色结点
r = x;
} else {
K k = x.key;
int h = x.hash;
Class<?> kc = null;
for (TreeNode<K, V> p = r;;) { // 从根据点遍历,寻找合适的位置,插入给定结点
int dir, ph;
K pk = p.key;
if ((ph = p.hash) > h) // 给定结点的hash值小于当前结点的hash值,往左子树寻找
dir = -1;
else if (ph < h) // 否则, 给定结点的hash值大于当前结点的hash值,往右子树寻找
dir = 1;
else if ((kc == null && (kc = comparableClassFor(k)) == null)
|| (dir = compareComparables(kc, k, pk)) == 0) // 如果hash值相等,则比较k值,用其Compare,如果还相等,则走tieBreakOrder方法
dir = tieBreakOrder(k, pk);
TreeNode<K, V> xp = p; // 暂存当前结点
if ((p = (dir <= 0) ? p.left : p.right) == null) { // 根据dir的值选取左右子结点,子结点不为空,继续循环寻找
x.parent = xp; // 已找到合适位置,作为当前结点的子结点
if (dir <= 0) // 小于0,使其成为左子结点
xp.left = x;
else // 否则,使其成为右子结点
xp.right = x;
r = balanceInsertion(r, x); // 插入后,平衡红黑树,使之满足红黑树性质
break; // 跳出
}
}
}
}
this.root = r; // 根节点
assert checkInvariants(root); // 检查一致性,红黑树及链表性质
}
find
final Node<K, V> find(int h, Object k) {
if (k != null) { // 如果k为空,直接返回null
for (Node<K, V> e = first; e != null;) { // 从首结点开始
int s;
K ek;
if (((s = lockState) & (WAITER | WRITER)) != 0) { // 如果有线程持有写锁,或有写线程在等待写锁,不再加读锁,而是以链表方式查找
if (e.hash == h && ((ek = e.key) == k || (ek != null && k.equals(ek))))
return e;
e = e.next;
} else if (U.compareAndSwapInt(this, LOCKSTATE, s, s + READER)) { // 否则,加读锁
TreeNode<K, V> r, p;
try {
p = ((r = root) == null ? null : r.findTreeNode(h, k, null)); // 以红黑树方式查找
} finally {
Thread w;
if (U.getAndAddInt(this, LOCKSTATE, -READER) == (READER | WAITER) && (w = waiter) != null) // 如果没有读线程了,并且有写线程在等待
LockSupport.unpark(w); // 唤醒阻塞的写线程
}
return p;
}
}
}
return null;
}
putTreeVal
final TreeNode<K, V> putTreeVal(int h, K k, V v) {
Class<?> kc = null;
boolean searched = false; // 如果遇见当前结点和目标结点发生碰撞的情况,且compare方法比较也相同,在进行调用tieBreakOrder方法之前,先搜索左子树或右子树一次,之后再遇见这种情况,则不必再搜索,因为那一次已经都搜索过了
for (TreeNode<K, V> p = root;;) { // 从根节点开始
int dir, ph;
K pk;
if (p == null) { // 如果根节点为空,则构建新结点,first和root都指向它
first = root = new TreeNode<K, V>(h, k, v, null, null);
break;
} else if ((ph = p.hash) > h) // 比较当前结点和目标结点的hash值
dir = -1; // 目前结点的hash值较小,则往左子树寻找
else if (ph < h)
dir = 1; // 否则,往右子树寻找
else if ((pk = p.key) == k || (pk != null && k.equals(pk))) // 如果hash相等,则比较key,若相等,则直接返回当前结点
return p; // 该结点的value值,则由调用方决定是否替换成新的value值
else if ((kc == null && (kc = comparableClassFor(k)) == null)
|| (dir = compareComparables(kc, k, pk)) == 0) { // hash碰撞(hash值相等,但key值不等),则采用compare方法比较
if (!searched) { // 如果kc为空,或者hash相等,key的Compare也相等,并且左子树或者右子树还没有搜索过,则搜索一次
TreeNode<K, V> q, ch;
searched = true;
if (((ch = p.left) != null && (q = ch.findTreeNode(h, k, kc)) != null)
|| ((ch = p.right) != null && (q = ch.findTreeNode(h, k, kc)) != null)) // 先搜索左子树,搜到则返回;否则搜索右子树,搜到则返回
return q;
}
dir = tieBreakOrder(k, pk); // 如果hash相等,key的Compare也相等,才采用此方法比较,此刻,dir要么为1,要么为-1
}
TreeNode<K, V> xp = p; // 记录当前结点
if ((p = (dir <= 0) ? p.left : p.right) == null) { // 根据dir的值,选择左子树或右子树
TreeNode<K, V> x, f = first; // 记录原首结点
first = x = new TreeNode<K, V>(h, k, v, f, xp); // 新结点从头部插入(创建新结点,first指向该新结点)
if (f != null)
f.prev = x; // 老的头节点prev属性指向新结点
if (dir <= 0)
xp.left = x; // 更新新结点为当前结点的左子结点
else
xp.right = x; // 更新新结点为当前结点的右子结点
if (!xp.red) // 如果当前结点是黑色结点,则直接插入结点(红色),满足红黑树性质
x.red = true;
else { // 否则,需要平衡红黑树(结合重新着色和旋转)
lockRoot(); // 平衡过程中,结点直接的树结构会发生改变,影响读操作,因此需要加锁,使读操作采用链表的方式进行
try {
root = balanceInsertion(root, x); // 平衡插入
} finally {
unlockRoot(); // 解锁
}
}
break;
}
}
assert checkInvariants(root); // 检测一致性
return null;
}
removeTreeNode
final boolean removeTreeNode(TreeNode<K, V> p) {
TreeNode<K, V> next = (TreeNode<K, V>) p.next; // 下一个结点
TreeNode<K, V> pred = p.prev; // 上一个结点,这是不带p玩的节奏啊
TreeNode<K, V> r, rl;
if (pred == null) // 如果p解释头结点
first = next; // next结点成为新的头节点
else
pred.next = next; // 否则,上一个结点和下一个结点直接相连
if (next != null)
next.prev = pred; // 相连
if (first == null) { // 如果p是唯一结点,置空root,直接返回
root = null;
return true;
}
if ((r = root) == null || r.right == null || // 规模较小,转成链表
(rl = r.left) == null || rl.left == null)
return true;
lockRoot(); // 否则,采用红黑树的删除方式,且需要加锁,同样因为考虑会影响读操作
try {
TreeNode<K, V> replacement; // 二叉树(红黑树也是二叉树)的删除,如果结点不是尾结点,则需要找到该结点的后继结点(未结点,可以直接删除)填补此位置
TreeNode<K, V> pl = p.left; // 左结点
TreeNode<K, V> pr = p.right; // 右结点
if (pl != null && pr != null) { // 如果都不为空
TreeNode<K, V> s = pr, sl;
while ((sl = s.left) != null) // 寻找p的后继结点,从p的右子结点开始,一直递归查找其左子结点,直至其没有左子结点
s = sl;
boolean c = s.red; // 后继结点是否是红色结点
s.red = p.red;
p.red = c; // p结点与其后继结点交换颜色
TreeNode<K, V> sr = s.right; // 后继结点的右子结点
TreeNode<K, V> pp = p.parent; // p的父节点
// s和p的结点位置互换
if (s == pr) { // 如果s是p的右子结点,说明s没有左子结点
p.parent = s; // p的父节点指针指向s
s.right = p; // s的右子结点指针指向p, 后面再处理其他指针
} else {
TreeNode<K, V> sp = s.parent; // s的父节点
if ((p.parent = sp) != null) { // p的父节点指针指向s的父节点
if (s == sp.left)
sp.left = p; // 如果s是其父节点的左子结点,则sp的左子结点指针指向p
else
sp.right = p; // 如果s是其父节点的右子结点,则sp的右子结点指针指向p
}
if ((s.right = pr) != null) // s的右子结点指针指向p的右子结点
pr.parent = s; // p的右子结点的指针指向s
}
p.left = null; // p的左子树置为空,同原来的s结点
if ((p.right = sr) != null) // 更新其他指针,使得互换完整,p的右子结点指针指向s的右子结点
sr.parent = p; // s的右子节点的父节点指针指向p
if ((s.left = pl) != null) // s的左子节点指针指向p的左子结点
pl.parent = s; // p的左子结点的父节点指针指向s
if ((s.parent = pp) == null) // 如果s没有父节点,那么s就是根节点
r = s; // root指针指向s
else if (p == pp.left) // 否则,继续更新其他指针,如果p是其原父节点的左子节点,那么p的原父节点的左子结点指针指向s
pp.left = s;
else // 否则,p的原父节点的右子节点指针指向s
pp.right = s;
if (sr != null) // 如果原s结点的右子结点sr不为空,则sr为最后空缺结点位置,平衡红黑树时,便以此位置结点(replacement)为基准,缺失此位置结点之后,再使得红黑树平衡
replacement = sr;
else // 否则,replacement是p结点
replacement = p;
} else if (pl != null) // 如果p的右子节点为空,则replacement是其左子结点
replacement = pl;
else if (pr != null) // 否则,是其右子结点
replacement = pr;
else
replacement = p; // 如果左右子结点均为空,replacement是p结点自己
if (replacement != p) { // 如果replacement不是p结点,在平衡红黑树之前删除p结点,目标结点会转移至replacement结点
TreeNode<K, V> pp = replacement.parent = p.parent; // replacement结点的父节点指针指向p的父节点
if (pp == null)
r = replacement; // 如果replacement结点的父节点为空,则为根节点,root指针指向它
else if (p == pp.left)
pp.left = replacement; // 否则,如果p为其父节点pp的左子结点,令pp的左子结点指针指向replacement
else // 如果p为其父节点pp的右子结点,令pp的右子结点指针指向replacement
pp.right = replacement;
p.left = p.right = p.parent = null; // 置空p的相关指针
}
root = (p.red) ? r : balanceDeletion(r, replacement); // 如果p为红色结点,则直接删除就好,否则,需要平衡红黑树
if (p == replacement) { // 如果replacement就是p结点,解除p的相关指针
TreeNode<K, V> pp;
if ((pp = p.parent) != null) { // p的父节点存在
if (p == pp.left) // 如果p是其父节点的左子结点,令其父节点的左子结点指针置空
pp.left = null;
else if (p == pp.right) // 否则,令其父节点的右子节点指针置空
pp.right = null;
p.parent = null; // 最后令p的父节点指针置空
}
}
} finally {
unlockRoot(); // 解除锁
}
assert checkInvariants(root); // 校验一致性
return false; // 不用进行红黑树转链表操作
}
读写锁
private final void lockRoot() { // 加锁
if (!U.compareAndSwapInt(this, LOCKSTATE, 0, WRITER)) // 加写锁
contendedLock(); // 如果CAS失败,以竞争的方式加锁
}
private final void unlockRoot() { // 解锁
lockState = 0;
}
private final void contendedLock() { // WRITER = 001; WAITER = 010; READER = 100; ~表示取反
boolean waiting = false;
for (int s;;) {
if (((s = lockState) & ~WAITER) == 0) { // ~WAITER = 101, 表示如果没有线程持有读锁,不会有线程持有写锁,因为与当前线程互斥
if (U.compareAndSwapInt(this, LOCKSTATE, s, WRITER)) { // CAS,设置写状态
if (waiting) // 如果设置过当前线程为等待线程
waiter = null; // 直接清除
return;
}
} else if ((s & WAITER) == 0) { // 如果有线程持有读锁,但没有别的写线程占据waiter
if (U.compareAndSwapInt(this, LOCKSTATE, s, s | WAITER)) { // 尝试设置waiter标志
waiting = true;
waiter = Thread.currentThread(); // 使自己成为等待获取锁的写线程
}
} else if (waiting) // 否则,使自己挂起
LockSupport.park(this);
}
}
ForwardingNode
static final class ForwardingNode<K, V> extends Node<K, V> {
final Node<K, V>[] nextTable; // 指向新数组
ForwardingNode(Node<K, V>[] tab) { // 构造方法
super(MOVED, null, null, null);
this.nextTable = tab;
}
Node<K, V> find(int h, Object k) { // 查找
outer: for (Node<K, V>[] tab = nextTable;;) { // 转移至新数组查找
Node<K, V> e;
int n;
if (k == null || tab == null || (n = tab.length) == 0 || (e = tabAt(tab, (n - 1) & h)) == null)
return null; // 没有则返回null
for (;;) {
int eh;
K ek;
if ((eh = e.hash) == h && ((ek = e.key) == k || (ek != null && k.equals(ek)))) // 找到直接返回
return e;
if (eh < 0) {
if (e instanceof ForwardingNode) { // 又遇见转发结点
tab = ((ForwardingNode<K, V>) e).nextTable; // 指向新数组
continue outer; // 类似于递归查找
} else
return e.find(h, k); // 调用结点的查找方法
}
if ((e = e.next) == null) // 没有则返回null
return null;
}
}
}
}
ReservationNode
static final class ReservationNode<K, V> extends Node<K, V> {
ReservationNode() {
super(RESERVED, null, null, null);
}
Node<K, V> find(int h, Object k) {
return null;
}
}
通用方法
spread
static final int spread(int h) { // 0111 1111 1111 1111 1111 1111 1111 1111
return (h ^ (h >>> 16)) & HASH_BITS;
}
tableSizeFor
private static final int tableSizeFor(int c) { // 计算table的实际size,返回值(x)是最小的且大小等于c的值,且x & (x - 1) == 0, 即是2的幂次方的值
int n = c - 1; // 定义Y位是从最高位开始第一个为1的位,Y越大,表示位数越高,int中,Y最大是32,即最左边的那个位
// 如果c已经是2的幂次方的值,那么n的Y位比c的小1,否则,与c的相等,使用n = c - 1,而不是直接使用c,目的是:如果c已经是2的幂次方的值时,直接返回c,而不是c << 1
// n右移1位,再与n作或运算,最后的结果是,Y位为1,(Y-1)位也为1了,
// 比如,n是 0000...1XXX XXXX...XXXX XXXX (X = 0或1),最后的结果是,
n |= n >>> 1; // 0000...11XX XXXX...XXXX XXXX
n |= n >>> 2; // 0000...1111 XXXX...XXXX XXXX
n |= n >>> 4; // 0000...1111 1111...XXXX XXXX
n |= n >>> 8; // 0000...1111 1111...1111 XXXX
n |= n >>> 16;// 0000...1111 1111...1111 1111
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1; // n + 1 = 0000...10...0
}
initTable
private final Node<K, V>[] initTable() {
Node<K, V>[] tab;
int sc;
while ((tab = table) == null || tab.length == 0) { // 由于是并发执行,所以采用死循环内执行CAS操作,保证只有一个线程执行此操作
if ((sc = sizeCtl) < 0) // 说明其他线程正在执行此操作,让出CPU即可
Thread.yield(); // 自旋一下
else if (U.compareAndSwapInt(this, SIZECTL, sc, -1)) { // CAS,成功则执行初始化操作
try {
if ((tab = table) == null || tab.length == 0) { // 再次判断,是因为,当前线程初始化时,有一个线程A进入了while里面(因为此时还未给table赋值)
// 但是初始化完成后,sizeCtl又恢复为原来的值,而A线程刚刚走到上面的if分支,由于不满足条件,
// 所以会走else
// if分支,是满足的。所以避免重复初始化,这里需要在判断一次
int n = (sc > 0) ? sc : DEFAULT_CAPACITY; // 计算容量
@SuppressWarnings("unchecked")
Node<K, V>[] nt = (Node<K, V>[]) new Node<?, ?>[n]; // 创建数组
table = tab = nt; // 给table赋值
sc = n - (n >>> 2); // sc = n - n/4 = 3n/4 = 0.75n 实际容量
}
} finally {
sizeCtl = sc; // 最后赋值给sizeCtl
}
break; // 初始化完成,跳出
}
}
return tab; // 返回
}
resizeStamp
static final int resizeStamp(int n) { // 不同长度数组的戳,唯一
return Integer.numberOfLeadingZeros(n) | (1 << (RESIZE_STAMP_BITS - 1));
}
treeifyBin
private final void treeifyBin(Node<K, V>[] tab, int index) { // 链表转为红黑树
Node<K, V> b;
int n, sc;
if (tab != null) {
if ((n = tab.length) < MIN_TREEIFY_CAPACITY) // 长度没有达到链表转红黑树容量,优先考虑扩容
tryPresize(n << 1);
else if ((b = tabAt(tab, index)) != null && b.hash >= 0) { // 确认是链表
synchronized (b) { // 加锁
if (tabAt(tab, index) == b) { // 再次确认
TreeNode<K, V> hd = null, // 指向头结点
tl = null; // 指向尾结点
for (Node<K, V> e = b; e != null; e = e.next) { // 遍历链表
TreeNode<K, V> p = new TreeNode<K, V>(e.hash, e.key, e.val, null, null); // 构建红黑树结点
if ((p.prev = tl) == null)
hd = p;
else
tl.next = p; // tl向后移动,以拼接结点
tl = p;
}
setTabAt(tab, index, new TreeBin<K, V>(hd)); // 设置hash桶,指向红黑树包装结点,在包装结点(TreeBin)内部构建红黑树
}
}
}
}
}
untreeify
static <K, V> Node<K, V> untreeify(Node<K, V> b) {
Node<K, V> hd = null, tl = null;
for (Node<K, V> q = b; q != null; q = q.next) { // 以链表方式遍历
Node<K, V> p = new Node<K, V>(q.hash, q.key, q.val, null); // 构建链表结点
if (tl == null)
hd = p; // 头结点
else
tl.next = p; // 尾结点
tl = p; // 更新尾结点
}
return hd;
}
基本操作
put
final V putVal(K key, V value, boolean onlyIfAbsent) {
if (key == null || value == null) // 参数校验
throw new NullPointerException();
int hash = spread(key.hashCode()); // 根据key的hashCode计算hash值
int binCount = 0; // hash桶存储的链表时,表示元素个数;若是红黑树,固定为2,既能保证进行扩容检查,又不触发链表转红黑树树操作
for (Node<K, V>[] tab = table;;) {
Node<K, V> f;
int n, i, fh;
if (tab == null || (n = tab.length) == 0)
tab = initTable(); // 初始化table
else if ((f = tabAt(tab, i = (n - 1) & hash)) == null) { // (n - 1) & hash, 计算table下标
if (casTabAt(tab, i, null, new Node<K, V>(hash, key, value, null))) // 数组索引i位置为空,则CAS该元素到此位置
break; // 成功则退出for循环
} else if ((fh = f.hash) == MOVED) // 如果是转发结点(ForwardingNode),说明此刻正在扩容
tab = helpTransfer(tab, f); // 帮助扩容
else {
V oldVal = null;
synchronized (f) { // 对桶的首结点加锁
if (tabAt(tab, i) == f) { // 万一扩容后,该索引位置已经替换为转发结点了,则重新开始循环
if (fh >= 0) { // 链表
binCount = 1; // 已存在首结点,这里为1
for (Node<K, V> e = f;; ++binCount) {
K ek;
if (e.hash == hash && ((ek = e.key) == key || (ek != null && key.equals(ek)))) { // 该结点“存在”
oldVal = e.val; // 取得老的val值
if (!onlyIfAbsent) // 根据条件
e.val = value; // 设置新的值
break;
}
Node<K, V> pred = e; // 备注前一个结点
if ((e = e.next) == null) { // 往后遍历,直到最后一个结点
pred.next = new Node<K, V>(hash, key, value, null); // 创建新的结点,并使得最后一个结点指向自己,使自己成为新的最后一个结点
break;
}
}
} else if (f instanceof TreeBin) { // 红黑树
Node<K, V> p;
binCount = 2; // 固定为2,既能保证进行扩容检查,又不触发链表转红黑树树操作
if ((p = ((TreeBin<K, V>) f).putTreeVal(hash, key, value)) != null) { // 调用红黑树的put方法
oldVal = p.val; // 取得老的val值
if (!onlyIfAbsent) // 根据条件
p.val = value; // 设置新的值
}
}
}
}
if (binCount != 0) {
if (binCount >= TREEIFY_THRESHOLD) // 达到阈值,则触发链表转红黑树操作
treeifyBin(tab, i); // 链表转红黑树
if (oldVal != null)
return oldVal; // 替换操作,无需更改计数值
break;
}
}
}
addCount(1L, binCount); // 计数加1
return null;
}
get
public V get(Object key) {
Node<K, V>[] tab;
Node<K, V> e, p;
int n, eh;
K ek;
int h = spread(key.hashCode()); // 计算hash值
if ((tab = table) != null && (n = tab.length) > 0 && (e = tabAt(tab, (n - 1) & h)) != null) { // 定位hash桶
if ((eh = e.hash) == h) { // 如果hash值相等
if ((ek = e.key) == key || (ek != null && key.equals(ek))) // 并且key相等,直接返回
return e.val;
} else if (eh < 0) // 如果hash值小于0,说明为特殊结点
return (p = e.find(h, key)) != null ? p.val : null; // 调用结点的查找方法
while ((e = e.next) != null) { // 链表方式查找
if (e.hash == h && ((ek = e.key) == key || (ek != null && key.equals(ek)))) // hash相等,key相等,返回,否则,循环继续
return e.val;
}
}
return null;
}
remove
remove
public V remove(Object key) {
return replaceNode(key, null, null); // 删除,用null替换原来的值
}
replaceNode
final V replaceNode(Object key, V value, Object cv) {
int hash = spread(key.hashCode()); // 计算hash值
for (Node<K, V>[] tab = table;;) {
Node<K, V> f;
int n, i, fh;
if (tab == null || (n = tab.length) == 0 || (f = tabAt(tab, i = (n - 1) & hash)) == null) // 找不到目标结点,直接跳出循环
break;
else if ((fh = f.hash) == MOVED) // 发现是转发结点,说明此时正在扩容
tab = helpTransfer(tab, f); // 去帮助扩容
else {
V oldVal = null;
boolean validated = false; // 操作是否有效
synchronized (f) { // 对hash桶第一个结点加锁
if (tabAt(tab, i) == f) { // 再次判定f是否是hash桶i的第一个结点
if (fh >= 0) { // 链表结点
validated = true; // 有效
for (Node<K, V> e = f, pred = null;;) {
K ek;
if (e.hash == hash && ((ek = e.key) == key || (ek != null && key.equals(ek)))) { // 找到目标结点
V ev = e.val;
if (cv == null || cv == ev || (ev != null && cv.equals(ev))) { // 判断value值是否被修改过,如果修改过(已经释放了锁,所以此线程能再获取到锁,其实是不同对象的),则退出
oldVal = ev; // 没有被修改过,记录老的value值
if (value != null)
e.val = value; // 替换成新值
else if (pred != null) // 如果新值为空,则删除此结点
pred.next = e.next; // 此结点的前驱结点和后继结点直接相连
else
setTabAt(tab, i, e.next); // 如果此结点没有前驱结点,说明它是hash桶的第一个结点,此时则设置其后继结点为hash桶第一个结点
}
break;
}
pred = e; // 记录上一个节点
if ((e = e.next) == null) // 右移遍历链表
break;
}
} else if (f instanceof TreeBin) { // 如果是红黑树结点
validated = true; // 有效
TreeBin<K, V> t = (TreeBin<K, V>) f; // 红黑树包装结点
TreeNode<K, V> r, p;
if ((r = t.root) != null && (p = r.findTreeNode(hash, key, null)) != null) { // 查找目标结点
V pv = p.val;
if (cv == null || cv == pv || (pv != null && cv.equals(pv))) { // 判断value值是否被修改过,如果修改过(可能已经释放了锁,所以此线程可以再获取到锁,其实是不同对象的),则退出
oldVal = pv; // 没有被修改过,记录老的value值
if (value != null)
p.val = value; // 替换成新值
else if (t.removeTreeNode(p)) // 如果新值为空,则删除此结点
setTabAt(tab, i, untreeify(t.first)); // 如果需要转换为链表,则执行红黑树转链表操作
}
}
}
}
}
if (validated) { // 如果操作有效
if (oldVal != null) {
if (value == null) // 并且是删除操作
addCount(-1L, -1); // 计数减一
return oldVal;
}
break;
}
}
}
return null;
}
扩容
addCount
private final void addCount(long x, int check) { // x:要更改的数目;check:判断是否扩容,小于0,无需扩容;小于等于1且有竞争计数线程,无需扩容;其余情况会考虑扩容
CounterCell[] as;
long b, s;
if ((as = counterCells) != null || !U.compareAndSwapLong(this, BASECOUNT, b = baseCount, s = b + x)) { // 首次计数(counterCells==null)且CAS成功,跳过if分支
CounterCell a;
long v;
int m;
boolean uncontended = true;
if (as == null || (m = as.length - 1) < 0 || (a = as[ThreadLocalRandom.getProbe() & m]) == null
|| !(uncontended = U.compareAndSwapLong(a, CELLVALUE, v = a.value, v + x))) { // 如果counterCells还没被初始化,或者当前线程hash的Cell还为被使用,或者CAS失败,走fullAddCount
fullAddCount(x, uncontended); // 优先将计数算在baseCount上,如果有竞争,便采用分槽计数,详见fullAddCount方法
return;
}
if (check <= 1) // 小于等于1且有竞争计数线程,无需扩容
return;
s = sumCount(); // 计算总数目
}
if (check >= 0) { // 检查扩容
Node<K, V>[] tab, nt;
int n, sc;
// 大于扩容阈值,table不为空,且长度小于最大值
while (s >= (long) (sc = sizeCtl) && (tab = table) != null && (n = tab.length) < MAXIMUM_CAPACITY) {
int rs = resizeStamp(n); // 计算当前数组的长度戳,防止重叠扩容
if (sc < 0) { // I
if ((sc >>> RESIZE_STAMP_SHIFT) != rs || sc == rs + 1 || sc == rs + MAX_RESIZERS
|| (nt = nextTable) == null || transferIndex <= 0) //II 如果不满足扩容条件,跳出循环
break;
if (U.compareAndSwapInt(this, SIZECTL, sc, sc + 1)) //III 扩容线程加1
transfer(tab, nt); // 执行转移任务
} else if (U.compareAndSwapInt(this, SIZECTL, sc, (rs << RESIZE_STAMP_SHIFT) + 2)) // 第一个执行转移任务的线程
transfer(tab, null);
s = sumCount(); // 计算总数
}
}
}
helpTransfer
final Node<K, V>[] helpTransfer(Node<K, V>[] tab, Node<K, V> f) { // 帮助扩容
Node<K, V>[] nextTab;
int sc;
if (tab != null && (f instanceof ForwardingNode) && (nextTab = ((ForwardingNode<K, V>) f).nextTable) != null) { // 根据f找到nextTable
int rs = resizeStamp(tab.length); // 计算当前扩容数组长度戳
while (nextTab == nextTable && table == tab && (sc = sizeCtl) < 0) {
if ((sc >>> RESIZE_STAMP_SHIFT) != rs || sc == rs + 1 || sc == rs + MAX_RESIZERS || transferIndex <= 0) // 如果不满足扩容条件,跳出循环
break;
if (U.compareAndSwapInt(this, SIZECTL, sc, sc + 1)) { // 扩容线程加1
transfer(tab, nextTab); // 执行转移任务
break;
}
}
return nextTab;
}
return table;
}
tryPresize
private final void tryPresize(int size) {
int c = (size >= (MAXIMUM_CAPACITY >>> 1)) ? MAXIMUM_CAPACITY : tableSizeFor(size + (size >>> 1) + 1); // 预计算下一次table容量
int sc;
while ((sc = sizeCtl) >= 0) {
Node<K, V>[] tab = table;
int n;
if (tab == null || (n = tab.length) == 0) { // 初始化table
n = (sc > c) ? sc : c;
if (U.compareAndSwapInt(this, SIZECTL, sc, -1)) { // CAS
try {
if (table == tab) {
@SuppressWarnings("unchecked")
Node<K, V>[] nt = (Node<K, V>[]) new Node<?, ?>[n]; // 新建table数组
table = nt;
sc = n - (n >>> 2); // 下一次table容量
}
} finally {
sizeCtl = sc;
}
}
} else if (c <= sc || n >= MAXIMUM_CAPACITY) // 已经扩容过了或超出最大容量
break;
else if (tab == table) {
int rs = resizeStamp(n); // 计算当前扩容数组长度戳
if (sc < 0) {
Node<K, V>[] nt;
if ((sc >>> RESIZE_STAMP_SHIFT) != rs || sc == rs + 1 || sc == rs + MAX_RESIZERS
|| (nt = nextTable) == null || transferIndex <= 0) // 如果不满足扩容条件,跳出循环
break;
if (U.compareAndSwapInt(this, SIZECTL, sc, sc + 1)) // 扩容线程加1
transfer(tab, nt); // 执行转移任务
} else if (U.compareAndSwapInt(this, SIZECTL, sc, (rs << RESIZE_STAMP_SHIFT) + 2)) // 第一个执行转移任务的线程
transfer(tab, null);
}
}
}
transfer
private final void transfer(Node<K, V>[] tab, Node<K, V>[] nextTab) {
int n = tab.length, stride; // n:数组长度,stride:步长,每个线程处理一段数据
if ((stride = (NCPU > 1) ? (n >>> 3) / NCPU : n) < MIN_TRANSFER_STRIDE) // 根据CPU的个数选择合适的步长,一个核心按8个线程算,线程越多,步长越小
stride = MIN_TRANSFER_STRIDE; // 最小步长
if (nextTab == null) { // 初始化
try {
@SuppressWarnings("unchecked")
Node<K, V>[] nt = (Node<K, V>[]) new Node<?, ?>[n << 1]; // 新数组长度是原来的两倍,扩容
nextTab = nt; // 赋值给nextTab
} catch (Throwable ex) { // 内存溢出情况
sizeCtl = Integer.MAX_VALUE;
return;
}
nextTable = nextTab; // nextTable变量指向新数组
transferIndex = n; // 转移索引,旧数组,从右往左,每次移动步长的距离,n -> 0
}
int nextn = nextTab.length; // 新数组的长度
ForwardingNode<K, V> fwd = new ForwardingNode<K, V>(nextTab); // 转发结点,旧数组里,每个hash桶处理完成后,替换成该结点,写操作遇见此结点就知道该桶已经转移完成,继续检查别的桶,读操作遇见它,就会根据此结点保存的信息,转移到新数组查询
boolean advance = true; // 表明任务是否向前推进,是,则定为下一个要处理的桶,否,则继续处理当前桶
boolean finishing = false; // 表明整个扩容任务是否完成,最后一个线程会处理一些收尾工作:重新扫一遍数组,完成遗漏的任务;更新属性的值
for (int i = 0, bound = 0;;) {
Node<K, V> f;
int fh;
while (advance) { // 任务向前推进
int nextIndex, nextBound;
if (--i >= bound || finishing) // i ∈ [bound, lastBound),如果i越界,或已经结束,不再推进
advance = false;
else if ((nextIndex = transferIndex) <= 0) { // transferIndex ∈ [0, length), 如果转移索引越界,不再推进
i = -1;
advance = false;
} else if (U.compareAndSwapInt(this, TRANSFERINDEX, nextIndex,
nextBound = (nextIndex > stride ? nextIndex - stride : 0))) { // CAS更新transferIndex减去stride步长
bound = nextBound; // 当前低边界
i = nextIndex - 1; // 当前高边界,从高(右)向低(左)移动
advance = false; // 先不推进索引,开始做任务
}
}
if (i < 0 || i >= n || i + n >= nextn) { // 边界检查,i ∈ [0, n), i + n要小于nextn,因为原数组i索引处的数据会被复制到新数组索引i和i + n处
int sc;
if (finishing) { // 如果任务将要结束,说明当前线程是最后一个扩容线程
nextTable = null; // 置空
table = nextTab; // 指向新数组
sizeCtl = (n << 1) - (n >>> 1); // 2n - n/2 = 2 * 3n/4
return;
}
if (U.compareAndSwapInt(this, SIZECTL, sc = sizeCtl, sc - 1)) { // 扩容线程个数减1,表明当前线程将要退出
if ((sc - 2) != resizeStamp(n) << RESIZE_STAMP_SHIFT) // 如果当前线程不是最后一个扩容线程
return; // 直接退出
finishing = advance = true; // 否则,最后一个线程执行收尾工作
i = n; // 从头再检查一遍
}
} else if ((f = tabAt(tab, i)) == null) // 如果该hash桶为空,则放入转移结点
advance = casTabAt(tab, i, null, fwd);
else if ((fh = f.hash) == MOVED) // 如果该hash桶里是转移结点,直接跳过
advance = true; // 任务向前推进
else {
synchronized (f) { // 对该hash桶上的首元素进行加锁,f不一定是桶的首元素,加锁期间,有可能有put操作,新结点是在头部插入的,所以加锁后需要再检查一遍
if (tabAt(tab, i) == f) { // 再次检查,f是否是i桶的首元素
Node<K, V> ln, hn;
if (fh >= 0) { // 链表
int runBit = fh & n; // 二进制第n位的01情况,以此分为两部分,分别复制到新数组的i桶和i + n桶处
Node<K, V> lastRun = f; // 执行链表中的某个结点,从这个结点开始,后面的所有结点的runBit相同,...->0->1->0->...>1->0->1(lastRun)->1->1, 或者...->0->1->0->...>1->1->0(lastRun)->0->0
for (Node<K, V> p = f.next; p != null; p = p.next) {
int b = p.hash & n; // 计算当前结点的"runBit"
if (b != runBit) { // 如果变了
runBit = b; // 更新runBit为当前结点的"runBit"
lastRun = p; // 指向当前结点
}
}
if (runBit == 0) { // 等于0的给ln
ln = lastRun; // lastRun及其之后的结点,不必复制,直接重用到新数组里
hn = null;
} else { // 等于1的给hn
hn = lastRun;
ln = null;
}
for (Node<K, V> p = f; p != lastRun; p = p.next) { // 遍历链表,根据runBit分成两部分
int ph = p.hash;
K pk = p.key;
V pv = p.val;
if ((ph & n) == 0)
ln = new Node<K, V>(ph, pk, pv, ln); // 从头部插入结点
else
hn = new Node<K, V>(ph, pk, pv, hn); // 从头部插入结点
}
setTabAt(nextTab, i, ln); // 新数组i桶
setTabAt(nextTab, i + n, hn); // 新数组i + n桶
setTabAt(tab, i, fwd); // 原数组i桶替换成转移结点
advance = true; // 当前桶任务完成,可以向前推进了
} else if (f instanceof TreeBin) { // 红黑树
TreeBin<K, V> t = (TreeBin<K, V>) f;
TreeNode<K, V> lo = null, // 指向runBit等于0的头结点
loTail = null; // 指向runBit等于0的尾结点
TreeNode<K, V> hi = null, // 指向runBit等于1的头结点
hiTail = null; // 指向runBit等于1的尾结点
int lc = 0, // 记录链表长度,据此决定是否要将红黑树转成链表
hc = 0; // 记录链表长度
for (Node<K, V> e = t.first; e != null; e = e.next) { // 以链表的方式遍历结点
int h = e.hash; // 当前结点的hash值
TreeNode<K, V> p = new TreeNode<K, V>(h, e.key, e.val, null, null); // 创建新结点,e的复制
if ((h & n) == 0) {
if ((p.prev = loTail) == null)
lo = p; // 头节点
else
loTail.next = p; // 尾节点的next属性指向新结点
loTail = p; // 更新尾结点
++lc; // 计数加1
} else { // 同上
if ((p.prev = hiTail) == null)
hi = p;
else
hiTail.next = p;
hiTail = p;
++hc;
}
}
ln = (lc <= UNTREEIFY_THRESHOLD) ? untreeify(lo) : (hc != 0) ? new TreeBin<K, V>(lo) : t; // 根据lc判断是否转成链表,如果hc为0,表明自己承接整个红黑树,直接指向t就可以了,也省了构造TreeBin的过程
hn = (hc <= UNTREEIFY_THRESHOLD) ? untreeify(hi) : (lc != 0) ? new TreeBin<K, V>(hi) : t; // 同上
setTabAt(nextTab, i, ln); // 新数组i桶
setTabAt(nextTab, i + n, hn); // 新数组i + n桶
setTabAt(tab, i, fwd); // 原数组i桶替换成转移结点
advance = true; // 当前桶任务完成,可以向前推进了
}
}
}
}
}
}
扩容重叠
如果不考虑stamp的差异
不同长度的数组对应不同的stamp,具体见resizeStamp方法
长度为n的数组扩容为2n,假设stamp_1表示为[n->2n]
长度为2n的数组扩容为4n,假设stamp_1表示为[2n->4n]
对于stamp_1版本的扩容,有A和B线程执行扩容,线程A执行过程中(I处,tab的长度为n)让出了CPU时间片,最后由线程B完成了扩容
由于stamp_1版本扩容已经完成,可进行stamp_2版本的扩容,且由C线程执行扩容,在此期间,线程A得到了时间片继续执行(II处,nt的长度为4n)
并继续执行至III处(下一步便是进入transfer方法),而线程C完成了扩容任务后,发现自己不是最后一个扩容线程(线程A才是,n->4n),直接就退出了,收尾工作交给A
线程来做,而A线程是基于长度为n的数组做的任务,对于stamp_2版本的2n->4n扩容任务可能会有遗漏,这边是扩容重叠导致的问题,也是resizeStamp存在的必要性
遍历器
TableStack
static final class TableStack<K, V> {
int length; // 长度
int index; // 索引
Node<K, V>[] tab; // 数组
TableStack<K, V> next; // 指向下一个
}
Traverser
类的定义
static class Traverser<K, V> {}
属性
Node<K, V>[] tab; // 当前数组,扩容时更新
Node<K, V> next; // 新数组,扩容完成后的数组
TableStack<K, V> stack, spare; // 保存/恢复转发结点
int index; // 下一个要读取hash桶的索引
int baseIndex; // 起始索引
int baseLimit; // 终止索引
final int baseSize; // 数组起始长度
构造方法
Traverser(Node<K, V>[] tab, int size, int index, int limit) { // 构造方法
this.tab = tab;
this.baseSize = size;
this.baseIndex = this.index = index;
this.baseLimit = limit;
this.next = null;
}
advance
final Node<K, V> advance() { // 遍历器指针往前移动下一个有效结点,并返回此结点,如果没有就返回null
Node<K, V> e;
if ((e = next) != null) // 如果e的下一个结点不为空,则指向此结点,即为有效结点,稍后返回
e = e.next;
for (;;) {
Node<K, V>[] t;
int i, n;
if (e != null) // e存在,直接返回
return next = e; // 更新next指针
if (baseIndex >= baseLimit || (t = tab) == null || (n = t.length) <= (i = index) || i < 0) // 边界检查
return next = null; // 结点不存在,直接返回null
if ((e = tabAt(t, i)) != null && e.hash < 0) { // 特殊结点
if (e instanceof ForwardingNode) { // 如果是转发结点
tab = ((ForwardingNode<K, V>) e).nextTable; // 指向新数组,遍历迁移至此
e = null; // 不可直接返回转发结点,置为空
pushState(t, i, n); // 入栈
continue; // 继续,遍历新桶
} else if (e instanceof TreeBin)
e = ((TreeBin<K, V>) e).first; // 如果是红黑树,指向头结点
else // 保留结点
e = null; // 置空
}
if (stack != null) // 出栈,或更新索引至i+len, 因为原数组i索引处的元素会复制到新数组i索引处和i+len索引处(len为原数组长度)
recoverState(n);
else if ((index = i + baseSize) >= n) // 更新元素索引(i++或i+len)
index = ++baseIndex;
}
}
pushState
private void pushState(Node<K, V>[] t, int i, int n) {
TableStack<K, V> s = spare; // 重用
if (s != null) // 不为空,其next指向spare
spare = s.next;
else // 否则新建一个
s = new TableStack<K, V>();
s.tab = t; // 数组信息
s.length = n; // 长度信息
s.index = i; // 索引信息
s.next = stack; // 指向栈顶
stack = s; // 更新栈顶
}
recoverState
private void recoverState(int n) {
TableStack<K, V> s;
int len;
while ((s = stack) != null && (index += (len = s.length)) >= n) { // 出栈
n = len;
index = s.index; // 索引信息
tab = s.tab; // 数组信息
s.tab = null; // 置空
TableStack<K, V> next = s.next; // 弹出
s.next = spare; // 重用
stack = next; // 更新栈顶
spare = s; // 执行弹出的栈元素
}
if (s == null && (index += baseSize) >= n) // 栈为空,索引处于新数组后半部分,则更新索引,原数组右移
index = ++baseIndex;
}
红黑树
性质
(1) 每个结点要么为红色要么为黑色。
(2) 根结点为黑色。
(3) 每个叶结点(NIL)是黑色的。
(4) 如果节点为红色,其子节点必须为黑色。
(5) 从一个节点到节点的后代节点的所有路径都包含相同数量的黑节点。
添加
Case 1
X的叔叔结点(U)是红色结点
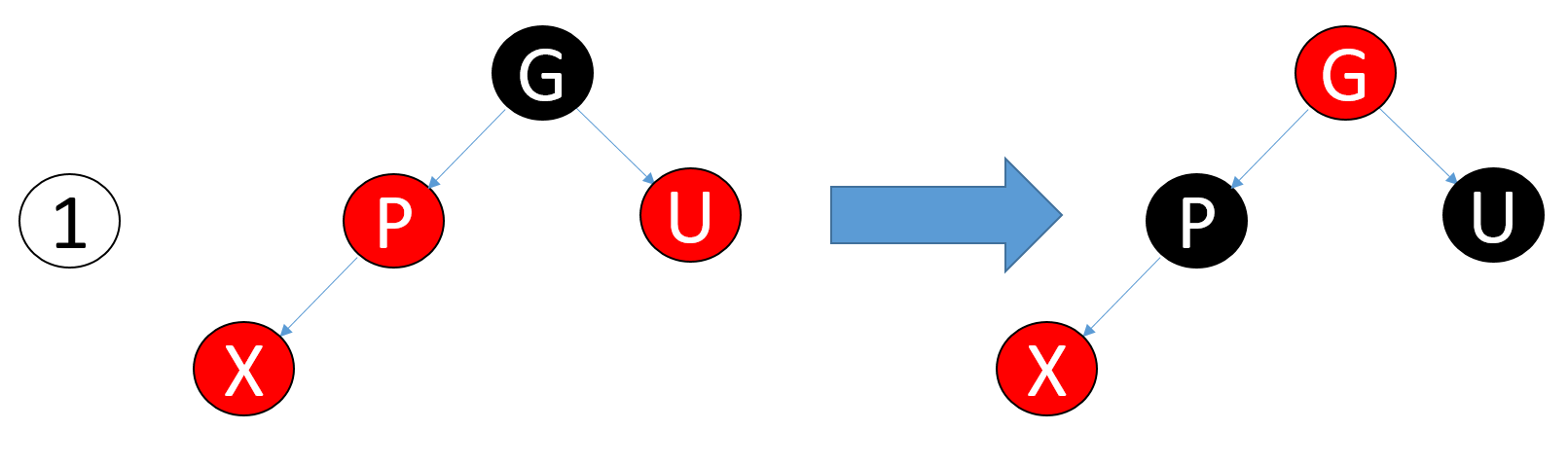
Case 2
X的叔叔节点(U)是黑色的,X是(P的)右子结点

Case 3
X的叔叔节点(U)是黑色的,X是(P的)左子结点
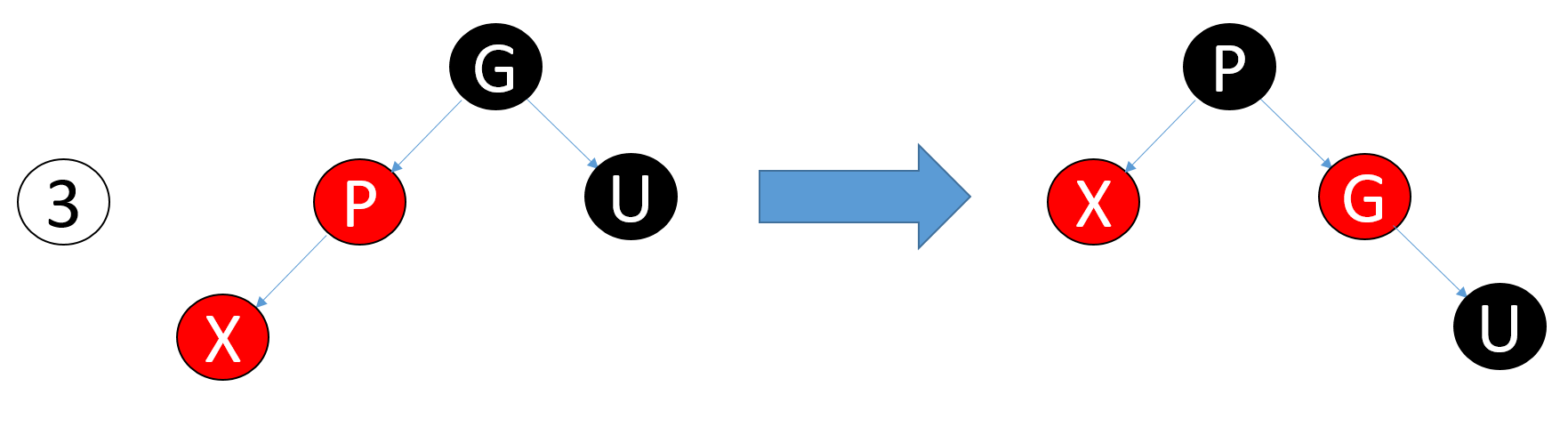
case1可以递归转化为case2或3。
case2可以转化为case3。
case3可以结束。
删除
Case 1
X的兄弟节点(B)是红色结点
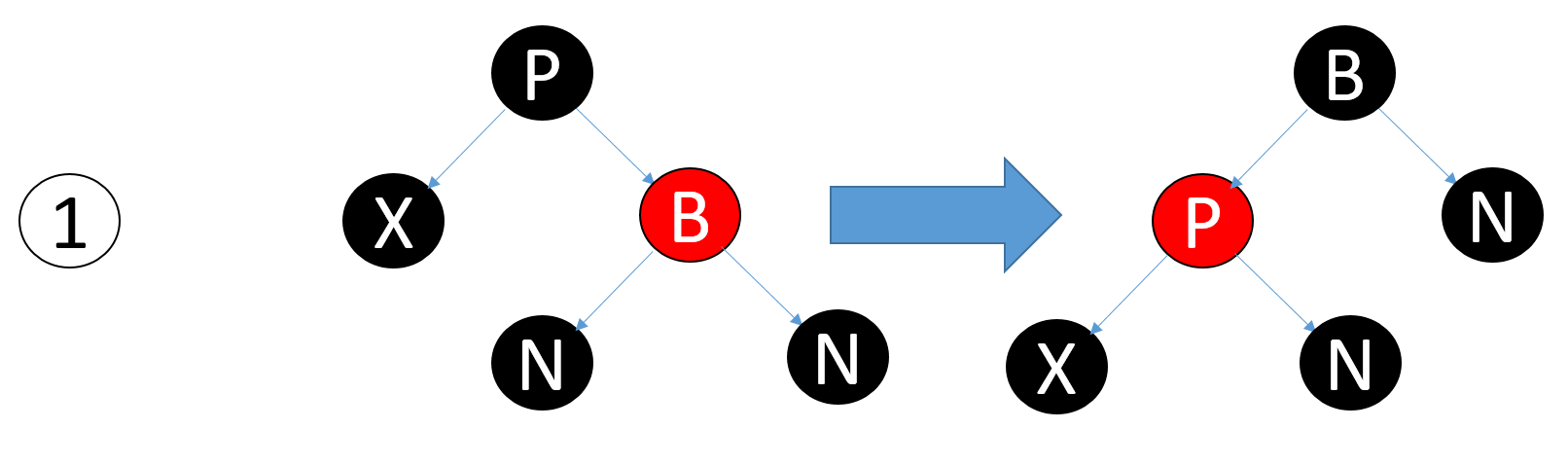
Case 2
X的兄弟节点(B)为黑色结点,B的两个子节点(N)为黑色结点

Case 3
X的兄弟节点(B)为黑色,B的左子结点为红色,右子结点为黑色结点
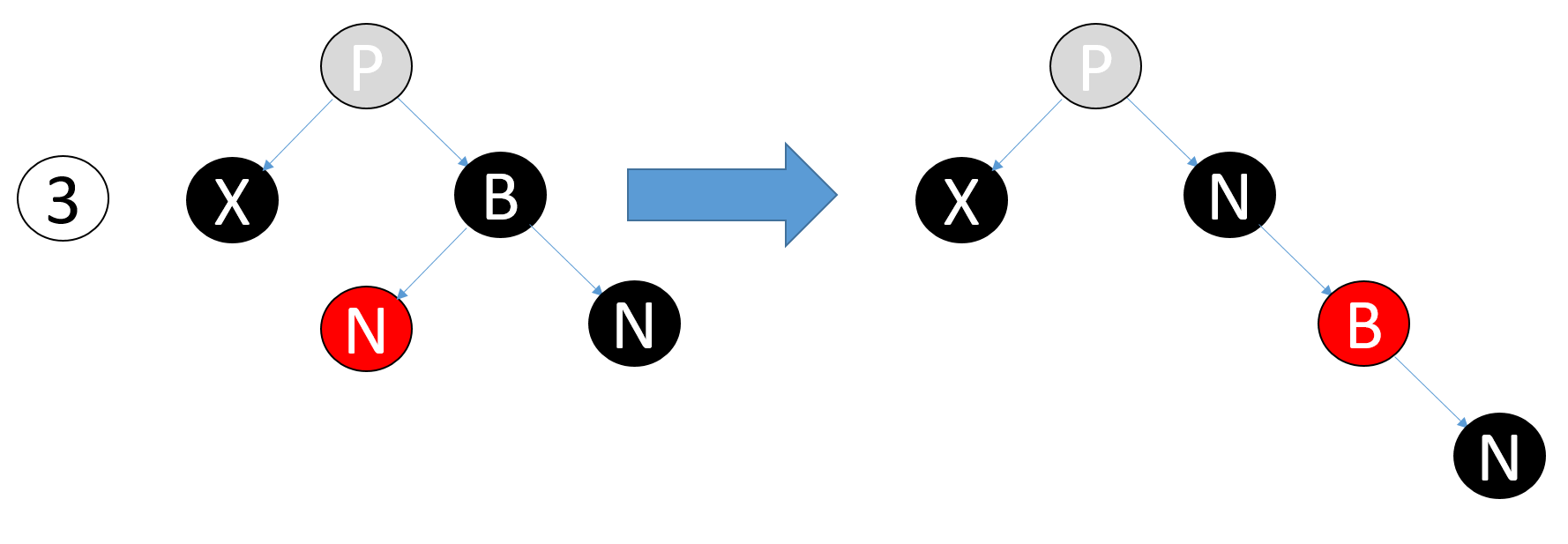
Case 4
X的兄弟节点(B)为黑色,B的右子节点为红色。
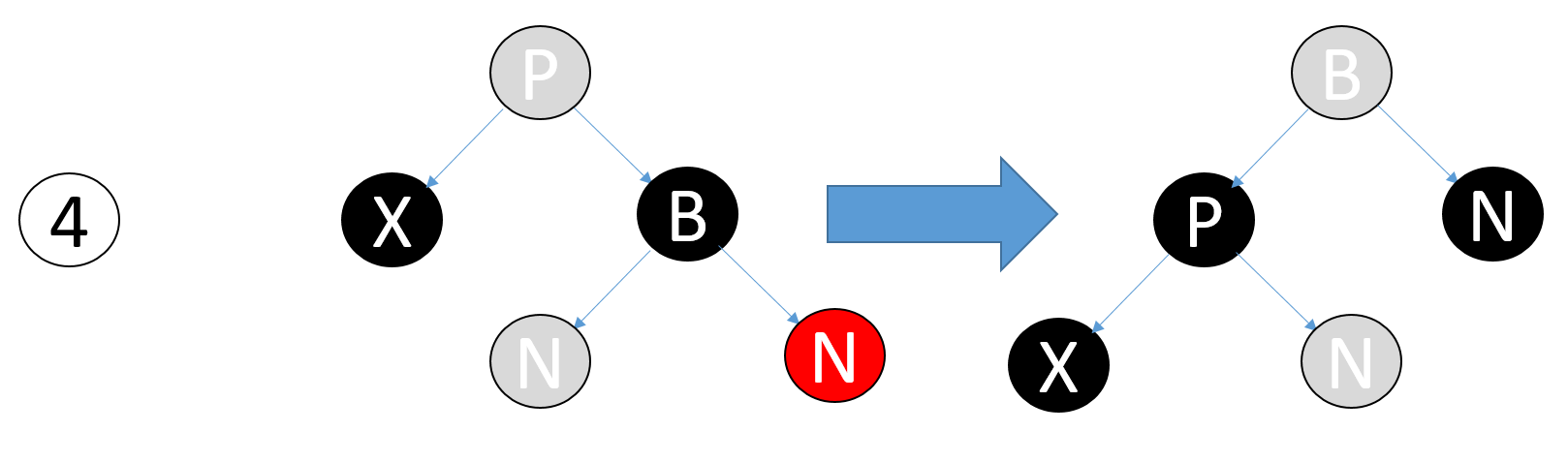
case1可以转化为案例2或3或4。
case2递归转化为案例3或4。
case3可以转化为案例4。
case4可以结束。
rotateLeft
static <K, V> TreeNode<K, V> rotateLeft(TreeNode<K, V> root, TreeNode<K, V> p) {
TreeNode<K, V> r, pp, rl;
if (p != null && (r = p.right) != null) { // 结点p及其右子结点r不为空
if ((rl = p.right = r.left) != null) // 结点r的左子结点不为空,并赋值给p的right指针,使其成为p的右子结点
rl.parent = p; // 更新rl的父节点为p
if ((pp = r.parent = p.parent) == null) // 使r的parent指针指向p的父节点,若为空,说明r已经是根节点,并赋值给root变量
(root = r).red = false;
else if (pp.left == p) // 否则,p的父节点pp存在,如果p是pp的左子结点,则更新pp的左子结点为r
pp.left = r;
else // 否则,更新pp的右子结点为r
pp.right = r;
r.left = p; // p成为r的左子结点
p.parent = r; // r成为p的父节点
}
return root; // 返回
}
rotateRight
static <K, V> TreeNode<K, V> rotateRight(TreeNode<K, V> root, TreeNode<K, V> p) { // 对称
TreeNode<K, V> l, pp, lr;
if (p != null && (l = p.left) != null) {
if ((lr = p.left = l.right) != null)
lr.parent = p;
if ((pp = l.parent = p.parent) == null)
(root = l).red = false;
else if (pp.right == p)
pp.right = l;
else
pp.left = l;
l.right = p;
p.parent = l;
}
return root;
}
balanceInsertion
static <K, V> TreeNode<K, V> balanceInsertion(TreeNode<K, V> root, TreeNode<K, V> x) { // 每插入一个结点,便执行此方法,以维持红黑树性质
x.red = true; // 新插入的结点一定是红色结点
for (TreeNode<K, V> xp, xpp, xppl, xppr;;) {
if ((xp = x.parent) == null) { // 如果x的父结点不存在,说明x是根结点
x.red = false; // 根节点颜色设为黑色,红黑树性质
return x;
} else if (!xp.red || (xpp = xp.parent) == null) // 如果x的父节点是黑色结点,则直接插入,符合红黑树性质;或者x的父节点xp是红色结点,但是xp的父结点为空,说明xp是根节点,那么也直接插入,因为别的线程稍后会把根节点xp置为黑色结点
return root;
if (xp == (xppl = xpp.left)) { // 如果x的父节点xp是xp的父结点的左子结点
if ((xppr = xpp.right) != null && xppr.red) { // case1,
// 如果x的叔叔结点xppr存在,且是红色结点
xppr.red = false; // 叔叔结点设置为黑色结点
xp.red = false; // 父亲结点设置为黑色结点
xpp.red = true; // 爷爷结点设置为红色结点
x = xpp; // 待平衡结点转移至爷爷结点,一直循环,直到根节点,或中途满足红黑树性质退出
} else {
if (x == xp.right) { // case2, x结点是其父节点的右子结点
root = rotateLeft(root, x = xp); // 左旋,且x指向了x的父节点
xpp = (xp = x.parent) == null ? null : xp.parent; // 更新xp和xpp,分别指向x的父节点和爷爷结点
}
if (xp != null) { // case3, x的父节点存在,且x的叔叔结点为黑色结点
xp.red = false; // x的父节点置为黑色结点
if (xpp != null) { // 如果爷爷结点也存在
xpp.red = true; // 置为红色结点
root = rotateRight(root, xpp); // 右旋
}
}
}
} else {
if (xppl != null && xppl.red) { // x为右子结点,对称
xppl.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
} else {
if (x == xp.left) {
root = rotateRight(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
if (xp != null) {
xp.red = false;
if (xpp != null) {
xpp.red = true;
root = rotateLeft(root, xpp);
}
}
}
}
}
}
balanceDeletion
static <K, V> TreeNode<K, V> balanceDeletion(TreeNode<K, V> root, TreeNode<K, V> x) {
for (TreeNode<K, V> xp, xpl, xpr;;) {
if (x == null || x == root) // x为空,或为根节点,直接返回
return root;
else if ((xp = x.parent) == null) { // x的父节点xp为空,说明x就是根节点
x.red = false; // 置为黑色结点
return x; // 返回
} else if (x.red) { // 如果x是红色结点,直接置为黑色,并返回
x.red = false;
return root;
} else if ((xpl = xp.left) == x) { // 如果x是xp的左子结点
if ((xpr = xp.right) != null && xpr.red) { // case1, 兄弟结点xpr不为空,且为红色
xpr.red = false; // 兄弟结点置为黑色结点
xp.red = true; // 父节点置为红色结点
root = rotateLeft(root, xp); // 左旋
xpr = (xp = x.parent) == null ? null : xp.right; // 更新xp和xpr, 分别为x的父节点和兄弟结点
}
if (xpr == null) // 如果兄弟结点为空,目标结点x转移至其父节点xp
x = xp;
else {
TreeNode<K, V> sl = xpr.left, sr = xpr.right;
if ((sr == null || !sr.red) && (sl == null || !sl.red)) { // case2, 两个侄子结点不存在,或为黑色结点
xpr.red = true; // 兄弟结点设置为红色结点,目标结点转移至其父节点
x = xp;
} else {
if (sr == null || !sr.red) { // case3, 右侄子结点不存在,或为黑色结点
if (sl != null) // 左侄子结点若存在,那么一定是红色结点
sl.red = false; // 置为黑色结点
xpr.red = true; // 兄弟结点置红色结点
root = rotateRight(root, xpr); // 右旋
xpr = (xp = x.parent) == null ? null : xp.right; // 更新xp和xpr,使得分别成为x的父节点和兄弟结点
}
if (xpr != null) { // case4, 兄弟结点不为空
xpr.red = (xp == null) ? false : xp.red; // 若父节点为空,则其兄弟结点置黑色,否则置为红色
if ((sr = xpr.right) != null) // 右侄子结点不为空
sr.red = false; // 置黑色结点
}
if (xp != null) { // 父节点xp不为空
xp.red = false; // 置为黑色结点
root = rotateLeft(root, xp); // 左旋
}
x = root;
}
}
} else { // 对称
if (xpl != null && xpl.red) {
xpl.red = false;
xp.red = true;
root = rotateRight(root, xp);
xpl = (xp = x.parent) == null ? null : xp.left;
}
if (xpl == null)
x = xp;
else {
TreeNode<K, V> sl = xpl.left, sr = xpl.right;
if ((sl == null || !sl.red) && (sr == null || !sr.red)) {
xpl.red = true;
x = xp;
} else {
if (sl == null || !sl.red) {
if (sr != null)
sr.red = false;
xpl.red = true;
root = rotateLeft(root, xpl);
xpl = (xp = x.parent) == null ? null : xp.left;
}
if (xpl != null) {
xpl.red = (xp == null) ? false : xp.red;
if ((sl = xpl.left) != null)
sl.red = false;
}
if (xp != null) {
xp.red = false;
root = rotateRight(root, xp);
}
x = root;
}
}
}
}
}
checkInvariants
static <K, V> boolean checkInvariants(TreeNode<K, V> t) { // 检查一致性
TreeNode<K, V> tp = t.parent, tl = t.left, tr = t.right, tb = t.prev, tn = (TreeNode<K, V>) t.next;
if (tb != null && tb.next != t) // 若前驱结点tb不为空,则tb的后继结点应为当前结点t
return false;
if (tn != null && tn.prev != t) // 若继结点tn不为空,则tn的前驱结点应为当前结点t
return false;
if (tp != null && t != tp.left && t != tp.right) // 若父节点tp不为空,则当前结点t要么是tp的左子结点,要么是tp的右子结点
return false;
if (tl != null && (tl.parent != t || tl.hash > t.hash)) // 若左子结点tl不为空,那么tl的父节点是当前结点,且hash值小于等于当前结点的hash值
return false;
if (tr != null && (tr.parent != t || tr.hash < t.hash)) // 若右子结点tr不为空,那么tr的父节点是当前结点,且hash值大于等于当前结点的hash值
return false;
if (t.red && tl != null && tl.red && tr != null && tr.red) // 如果当前结点是红色结点,则它的两个子结点都不能为红色,红黑树的性质:如果一个节点是红色的,则它的子节点必须是黑色的,条件应为:t.red && ((tl != null && tl.red) || (tr != null && tr.red))
return false;
if (tl != null && !checkInvariants(tl)) // 如果左子结点不为空,则检查左子树
return false;
if (tr != null && !checkInvariants(tr)) // 如果右子结点不为空,则检查右子树
return false;
return true;
}
分槽计数
fullAddCount
private final void fullAddCount(long x, boolean wasUncontended) {
int h;
if ((h = ThreadLocalRandom.getProbe()) == 0) { // 给当前线程生成一个非0的hash值
ThreadLocalRandom.localInit(); // force initialization
h = ThreadLocalRandom.getProbe();
wasUncontended = true;
}
boolean collide = false; // hash取模得到的hash桶不为空,此值设为true,有扩容意向
for (;;) {
CounterCell[] as;
CounterCell a;
int n;
long v;
if ((as = counterCells) != null && (n = as.length) > 0) { // 已经初始化过了
if ((a = as[(n - 1) & h]) == null) { // hash桶(cell)为空
if (cellsBusy == 0) { // 并且没有争用线程
CounterCell r = new CounterCell(x); // 创建一个计数单元
if (cellsBusy == 0 && U.compareAndSwapInt(this, CELLSBUSY, 0, 1)) { // 尝试占有此hash桶
boolean created = false;
try {
CounterCell[] rs;
int m, j;
if ((rs = counterCells) != null && (m = rs.length) > 0 && rs[j = (m - 1) & h] == null) { // 加锁后,再次检查
rs[j] = r; // 计数单元占领此桶
created = true; // 创建成功
}
} finally {
cellsBusy = 0; // 释放锁
}
if (created) // 成功,则跳出循环
break;
continue; // 否则继续循环计数
}
}
collide = false; // 因为上次此桶还为空,暂时不考虑扩容操作
} else if (!wasUncontended) // 说明有竞争,如果没有标记过,则标记为true
wasUncontended = true; // 重新计算线程的hash值,寻找别的hash桶
else if (U.compareAndSwapLong(a, CELLVALUE, v = a.value, v + x)) // 尝试CAS更新
break; // 成功则跳出
else if (counterCells != as || n >= NCPU) // 有线程已经进行了扩容,或者数组长度达到最大值(大于CPU的核心数,即线程数,已经没有扩容的必要了)
collide = false; // 清除扩容意向
else if (!collide) // Cell不为空,且CAS失败,标记扩容意向
collide = true;
else if (cellsBusy == 0 && U.compareAndSwapInt(this, CELLSBUSY, 0, 1)) { // 尝试加锁
try {
if (counterCells == as) { // 扩容
CounterCell[] rs = new CounterCell[n << 1]; // 2倍
for (int i = 0; i < n; ++i)
rs[i] = as[i]; // 复制
counterCells = rs; // 指向新数组
}
} finally {
cellsBusy = 0; // 解锁
}
collide = false; // 清除扩容意向
continue; // 从头继续
}
h = ThreadLocalRandom.advanceProbe(h); // 从新计算hash值
} else if (cellsBusy == 0 && counterCells == as && U.compareAndSwapInt(this, CELLSBUSY, 0, 1)) { // 初始化
boolean init = false;
try { // 初始化table
if (counterCells == as) {
CounterCell[] rs = new CounterCell[2]; // 初始长度为2
rs[h & 1] = new CounterCell(x); // 对其中一个单元进行计数操作
counterCells = rs;
init = true; // 初始化完成
}
} finally {
cellsBusy = 0; // 解锁
}
if (init) // 成功,则跳出循环
break;
} else if (U.compareAndSwapLong(this, BASECOUNT, v = baseCount, v + x)) // 直接加在baseCount上面
break; // 成功则跳出循环,否则继续分槽计数
}
}
行文至此结束。
尊重他人的劳动,转载请注明出处:http://www.cnblogs.com/aniao/p/aniao_chm.html
【JUC源码解析】ConcurrentHashMap的更多相关文章
- 【JUC源码解析】ScheduledThreadPoolExecutor
简介 它是一个线程池执行器(ThreadPoolExecutor),在给定的延迟(delay)后执行.在多线程或者对灵活性有要求的环境下,要优于java.util.Timer. 提交的任务在执行之前支 ...
- 【JUC源码解析】Exchanger
简介 Exchanger,并发工具类,用于线程间的数据交换. 使用 两个线程,两个缓冲区,一个线程往一个缓冲区里面填数据,另一个线程从另一个缓冲区里面取数据.当填数据的线程将缓冲区填满时,或者取数据的 ...
- 【JUC源码解析】SynchronousQueue
简介 SynchronousQueue是一种特殊的阻塞队列,该队列没有容量. [存数据线程]到达队列后,若发现没有[取数据线程]在此等待,则[存数据线程]便入队等待,直到有[取数据线程]来取数据,并释 ...
- 【JUC源码解析】ForkJoinPool
简介 ForkJoin 框架,另一种风格的线程池(相比于ThreadPoolExecutor),采用分治算法,工作密取策略,极大地提高了并行性.对于那种大任务分割小任务的场景(分治)尤其有用. 框架图 ...
- 【JUC源码解析】DelayQueue
简介 基于优先级队列,以过期时间作为排序的基准,剩余时间最少的元素排在队首.只有过期的元素才能出队,在此之前,线程等待. 源码解析 属性 private final transient Reentra ...
- 【JUC源码解析】CyclicBarrier
简介 CyclicBarrier,一个同步器,允许多个线程相互等待,直到达到一个公共屏障点. 概述 CyclicBarrier支持一个可选的 Runnable 命令,在一组线程中的最后一个线程到达之后 ...
- 【JUC源码解析】ConcurrentLinkedQueue
简介 ConcurrentLinkedQueue是一个基于链表结点的无界线程安全队列. 概述 队列顺序,为FIFO(first-in-first-out):队首元素,是当前排队时间最长的:队尾元素,当 ...
- Java泛型底层源码解析--ConcurrentHashMap(JDK1.7)
1. Concurrent相关历史 JDK5中添加了新的concurrent包,相对同步容器而言,并发容器通过一些机制改进了并发性能.因为同步容器将所有对容器状态的访问都串行化了,这样保证了线程的安全 ...
- Jdk1.6 JUC源码解析(12)-ArrayBlockingQueue
功能简介: ArrayBlockingQueue是一种基于数组实现的有界的阻塞队列.队列中的元素遵循先入先出(FIFO)的规则.新元素插入到队列的尾部,从队列头部取出元素. 和普通队列有所不同,该队列 ...
随机推荐
- 1、RabbitMQ入门
RabbitMQ 可以参考官网进行学习! 开发语言:Erlang – 面向并发的编程语言. AMQP:是消息队列的一个协议. mysql 是 java 写的吗?不是 那么 java 能不能访问?可以, ...
- 3、Dubbo-环境搭建
官方推荐使用 Zookeeper 注册中心 3.1).[windows]-安装zookeeper 开发中均在Linux中安装!!! 1.下载zookeeper 网址 https://archive.a ...
- jq页面加载问题
Window.onload=function(){ //页面加载,不能同时编写多个,最后面的会覆盖前面的 } $(document).ready(function(){ //页面加载,能同时编写多 ...
- Apollo GPS调试笔记
前言:在Apollo美研团队的支持下,最近完成了Apollo推荐的Novatel PP7与我们的基站调试,在这里对Apollo的笔记做一个补充,希望以后的开发者不用在踩我们踩过的坑. 在自己调导航(h ...
- VC++6.0中碰到Cannot access the ClassView information file.ClassView information will not be avaible.的解决方法
一般情况下是由于类视图文件损坏了,这是经常会发生的现象. 解决步骤: 1.关闭工程,2.删除工程下.clw .ncb 文件及/debug目录,3.重建工程build all. 具体解释如下: dsp ...
- .NET完全手动搭建三层B/S架构
简介:三层架构(3-tier application) 通常意义上的三层架构就是将整个业务应用划分为:表现层(WebUI).业务逻辑层(BusinessLogicLayer).数据访问层(DataAc ...
- 【luogu P3959 宝藏】 题解
题目链接:https://www.luogu.org/problemnew/show/P3959 我只是心血来潮想学SA(考场上骗分总行吧). 这个题可以状压DP.爆搜+剪枝.有意思的还是随机化搜索( ...
- Android-应用性能测试
参考了文章:http://www.cnblogs.com/mliangchen/p/5125114.html 问题一:使用真机在DDMS下,查看不到应用进程,logcat也不全 最后,只能使用Geny ...
- HDU 1142 A Walk Through the Forest(最短路+记忆化搜索)
A Walk Through the Forest Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Jav ...
- String系列01 - String 60%
1.String简介 String类实现CharSequence接口.(同时,实现Serializable, Comparable 接口). String类使用final修饰符,为final类,不可被 ...
