数据结构与算法-图的最短路径Dijkstra

一  无向图单源最短路径，Dijkstra算法

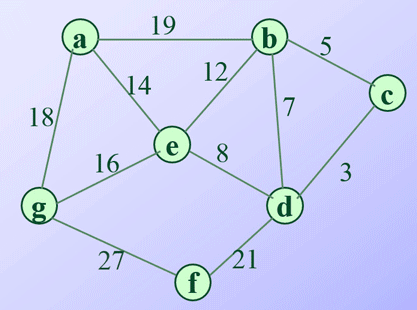
计算源点a到图中其他节点的最短距离，是一种贪心算法。利用局部最优，求解全局最优解。

设立一个visited访问和dist距离数组，在初始化后每一次收集一个当前最短的节点cur并将其标记为visited，然后更新这个节点的未被收集临近节点的dist值 [ if ( visited[t] != True && (dis[cur]+ Graph[cur][t]) < dis[t] )  ]，直到所有节点被访问。查找dist中的最短路径节点，可使用最小堆或二项堆，降低时间复杂度。

二

 /* Dijkstra of shortest path of single source in graph */

#include <stdio.h>
#define MAX 100
/* int as +/-[2^31] --> 0-2147483647 */
#define INFIN 2147483647
enum BOOL {
    False, True
};

int Graph[MAX][MAX]; /* matrix of graph */
int dis[MAX];        /* distance from origin other nodes */
BOOL visited[MAX]; 

void Dijkstra( int v0 , int N);

int main(int argc, char *argv[])
{
    int i, j, k;
    int N, M, src, dst, distance;
    int start;

    /* input vertex number and edge number */
    scanf("%d%d", &N, &M);
    /* Initialize the vertax and edge of graph matrix */
    for ( i = ; i < N; i++ ) {
        for ( j = ; j < N; j++ ) {
            if ( i == j  ) {
                /* edge of vertax itself*/
                Graph[i][j] = ;
            } else {
                /* all edge large than 0, unless it's unkonwn */
                Graph[i][j] = INFIN;
            }
        }
    }

    /* Init the orignal graph edge */
    printf("Please input the init edge\n");
    for ( k = ; k < M; k++ ) {
        scanf("%d%d%d", &src, &dst, &distance);
        Graph[src][dst] = distance;
    }

    printf("Please input the start vertax:");
    scanf("%d", &start);
    if ( start >=  ) {
        Dijkstra( start, N);
        printf("Distance from %d to others as follows:\n", start);
        printf("src --> dst\n");

        for ( k = ; k < N; k++ ) {
            printf("%d-->%d cost:%d ", start, k, dis[k]);
            if ( k >  && (k % ) ==  ) {
                printf("\n");
            }

        }
    }
    return ;
}

void Dijkstra( int v0, int N )
{
    /* Init dis */
    int i, j, k, t; /* cur represent current vertax */
    int cur, mini_dis;
    for ( i = ; i < N; i++ ) {
        dis[i] = Graph[v0][i];
        visited[i] = False;
    }
    cur = v0;
    visited[v0] = True;
    mini_dis = INFIN;

    /* find dis to another MAX-1 points */
    for ( j = ; j < N; j++ ) {
        /* for simple use，iterate the array to find a shortest*/
        for ( k = ; k < N; k++ ) {
            if ( visited[k] != True &&
                 dis[k] < mini_dis ) {
                 mini_dis = dis[k];
                 cur = k;
            }
        }
        visited[cur] = True;

        /* Update the correlated dis with current shortest point */
        for ( t = ; t < N; t++ ) {
            if ( Graph[cur][t] < dis[t] ) {
                /* update if dis to [cur veratx + edge] < [dis to t] */
                if ( visited[t] != True &&
                    (dis[cur]+ Graph[cur][t]) < dis[t] ) {
                    dis[t] = dis[cur] + Graph[cur][t];
                }
            }
        }
    }
}