洛谷P1265 公路修建（Prim）

To 洛谷.1265 公路修建

题目描述

某国有n个城市，它们互相之间没有公路相通，因此交通十分不便。为解决这一“行路难”的问题，政府决定修建公路。修建公路的任务由各城市共同完成。

修建工程分若干轮完成。在每一轮中，每个城市选择一个与它最近的城市，申请修建通往该城市的公路。政府负责审批这些申请以决定是否同意修建。

政府审批的规则如下：

（1）如果两个或以上城市申请修建同一条公路，则让它们共同修建；

（2）如果三个或以上的城市申请修建的公路成环。如下图，A申请修建公路AB，B申请修建公路BC，C申请修建公路CA。则政府将否决其中最短的一条公路的修建申请；

（3）其他情况的申请一律同意。

一轮修建结束后，可能会有若干城市可以通过公路直接或间接相连。这些可以互相：连通的城市即组成“城市联盟”。在下一轮修建中，每个“城市联盟”将被看作一个城市，发挥一个城市的作用。

当所有城市被组合成一个“城市联盟”时，修建工程也就完成了。

你的任务是根据城市的分布和前面讲到的规则，计算出将要修建的公路总长度。

输入输出格式

输入格式：

第一行一个整数n，表示城市的数量。(n≤5000)

以下n行，每行两个整数x和y，表示一个城市的坐标。(-1000000≤x，y≤1000000)

输出格式：

一个实数，四舍五入保留两位小数，表示公路总长。（保证有惟一解）

输入输出样例

输入样例#1：

4
0 0
1 2
-1 2
0 4

输出样例#1：

6.47

说明

修建的公路如图所示：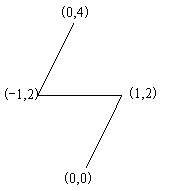

思路：

　　规则2是没有用的，因为不可能存在三个及以上个城市形成环。按“轮”处理也没有必要，因此这就成了一道求最小生成树的题。

　　如果用Kruskal需用5000*5000的矩阵先计算出边，肯定是超内存的。所以选择Prim，在求最小生成树过程中计算两点距离。

代码：

 #include<cmath>
 #include<cstdio>
 using namespace std;
 const int N=;
 
 int n,x[N],y[N];
 double Ans,Min[N];
 bool vis[N];
 
 void read(int &now)
 {
     now=;bool f=;char c=getchar();
     while(c>''||c<'')
     {
         if(c=='-')f=;
         c=getchar();
     }
     while(c>=''&&c<='')now=(now<<)+(now<<)+c-'',c=getchar();
     now= f?-now:now;
 }
 
 double Calu(int a1,int b1,int a2,int b2)
 {
     return sqrt((double)(a1-a2)*(a1-a2)+(double)(b1-b2)*(b1-b2));
     //因为这里的自乘很可能爆int，改成longlong也不是不可以但耗内存,so 转换成double
 }
 
 int main()
 {
     read(n);
     for(int i=;i<=n;++i)
       read(x[i]),read(y[i]),Min[i]=1e9;
     Min[]=;
     for(int i=;i<=n;++i)
     {
         double k=1e9;int cur=;
         for(int j=;j<=n;++j)
           if(!vis[j] && k>Min[j])
           {
                 k=Min[j];cur=j;
           }
         vis[cur]=;
         Ans+=k;
         for(int j=;j<=n;++j)
         {
             if(vis[j])continue;
             double t=Calu(x[cur],y[cur],x[j],y[j]);
             if(Min[j]>t)
               Min[j]=t;
         }
     }
     printf("%.2lf",Ans);
     return ;
 }