网络流24题 P2754 [CTSC1999]家园

思路

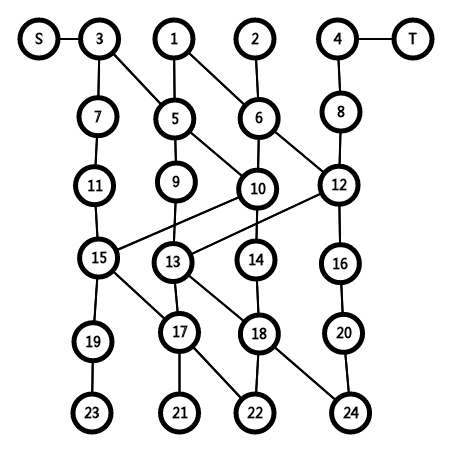
如图,建立分层图跑dinic

每次在残余网络里加边继续跑

跑到ans>=k时候的i就是答案

诶呀啊，忘记弄箭头了，最后一列是向上的箭头，不过聪明的你们应该没啥影响

代码

#include <bits/stdc++.h>
#define FOR(i,a,b) for(int i=a;i<=b;++i)
using namespace std;
const int N = 1e6 + 7;
const int inf = 0x3f3f3f3f;
int read() {
    int x=0,f=1;char s=getchar();
    for(;s>'9'||s<'0';s=getchar()) if(s=='-') f = -1;
    for(;s>='0'&&s<='9';s=getchar()) x = x*10 + s - '0';
    return x*f;
}
int n, m, k, h[100], S, T;
std::vector<int> G[100];
struct node {
    int v, nxt, cap;
}e[N];
int head[N], tot = 1;
void add_edge(int u, int v, int cap) {
    e[++tot].v = v;
    e[tot].cap = cap;
    e[tot].nxt = head[u];
    head[u] = tot;
}
int dis[N];
queue <int> Q;
bool bfs() {
    memset(dis, -1, sizeof(dis));
    while(!Q.empty()) Q.pop();
    dis[S] = 0;
    Q.push(S);
    while(!Q.empty()) {
        int u = Q.front();
        Q.pop();
        for(int i = head[u]; i;i = e[i].nxt) {
            int v = e[i].v;
            if(dis[v] == -1 && e[i].cap) {
                dis[v] = dis[u] + 1;
                Q.push(v);
            }
        }
    }
    return dis[T] != -1;
}
int dfs(int now, int f) {
    if(now == T) return f;
    int rest = f;
    for(int i = head[now]; i;i = e[i].nxt) {
        int v = e[i].v;
        if(dis[v] == dis[now] + 1 && e[i].cap && rest) {
            int t = dfs(v, min(e[i].cap, rest));
            if(!t) dis[v] = 0;
            e[i].cap -= t;
            e[i^1].cap += t;
            rest -= t;
        }
    }
    return f-rest;
}
namespace bcj {
    int siz[N], f[N];
    int find(int x) {
        return x == f[x] ? x : f[x] = find(f[x]);
    }
    void uu(int x, int y) {
        int fx = find(x), fy = find(y);
        if(siz[fx] <= siz[fy]) {
            f[fx] = fy;
            if(siz[fx] == siz[fy]) siz[fy] ++;
        } else f[fy] = fx;
    }
}
int main() {
    n = read() ,m = read(), k = read();
    S = 5e5+1, T = 5e5+2;
    FOR(i,1,1000) bcj::f[i] = i;
    FOR(i, 1, m) {
        h[i] = read();
        int x = read();
        FOR(j, 1, x) {
            int tmp = read();
            if(tmp==0) tmp = n+1;
            if(tmp==-1) tmp = n+2;
            G[i].push_back(tmp);
        }
    }
    FOR(i,1,m) {
        for(std::vector<int>::iterator it = G[i].begin() + 1; it != G[i].end(); ++ it) {
            bcj::uu(*it, *(it-1));
        }
    }
    if(bcj::find(n+1) != bcj::find(n+2)) {puts("0"); return 0;}
    int ans = 0,i = 1;
    add_edge(S, n + 1, inf);
    add_edge(n + 1, S, 0);

    add_edge(n + 2, T, inf);
    add_edge(T, n + 2, 0);
    for(;; ++i) {
        // my -> my
        FOR(j, 1, n + 1) {
            add_edge(j + (i-1) * (n + 2), j + i * (n + 2), inf);
            add_edge(j + i * (n + 2), j + (i-1) * (n + 2), 0);
        }
        add_edge((i + 1) * (n + 2), i * (n + 2), inf);
        add_edge(i * (n + 2), (i + 1) * (n + 2), 0);
        // go go go
        FOR(j, 1, m) {
            int a = i % G[j].size() - 1;
            int b = i % G[j].size();
            a= a<0 ? G[j].size()-1 : a;
            a =G[j][a] + (i - 1) * (n + 2);
            b =G[j][b] + i * (n + 2);
            add_edge(a, b, h[j]);
            add_edge(b, a, 0);
        }
        while(bfs()) ans += dfs(S,inf);
        if(ans >= k) break;
    }
    printf("%d\n", i);
    return 0;
}