浅谈FFT、NTT和MTT

前言

\(\text{FFT}\)（快速傅里叶变换）是 \(O(n\log n)\) 解决多项式乘法的一个算法，\(\text{NTT}\)（快速数论变换）则是在模域下的，而 \(\text{MTT}\)（毛神仙对\(\text{FFT}\)的精度优化算法）可以针对任意模数。本文主要讲解这三种算法，具体的应用还请参考我博客内的题解。

正文

FFT-快速傅里叶变换

学习这个算法可以借助《算法导论》，当然算导上的东西需要耐心才能啃下来。这里只是概括一下算导上的介绍，并加入一些个人的见解。下面逐步介绍这个算法。

复数

如果学过的话可以跳过。实数可以一一对应数轴上的点，那么复数就可以一一对应平面直角坐标系上的点。对应 \(x\) 轴上的点的就是我们熟悉的实数，而外面的就是虚数。其中 \((0,1)\) 这个点对应的数记作 \(i\) ，即 \(\sqrt{-1}\)，它表示虚数单位。复数可以表示成 \(a+ib\) 的形式，其中 \(a,b\) 为实数。

极坐标表示法下的乘法

\((a,\alpha)\cdot(b,\beta)=(ab,\alpha+\beta)\)

证明如下：

\[\begin{align}{}
&(a,\alpha)\cdot(b,\beta) \notag\\
=&ab(\cos\alpha+i\sin\alpha)(\cos\beta+i\sin\beta)\notag\\
=&ab[\cos\alpha\cos\beta+i(\sin\alpha\cos\beta+\cos\alpha\sin\beta)-\sin\alpha\sin\beta]\notag\\
=&ab[\cos(\alpha+\beta))+i\sin(\alpha+\beta)]\notag\\
=&(ab,\alpha+\beta)\notag
\end{align}
\]

代数表示法下的乘法

\((a+ib)\cdot(c+id)=ac-bd+i(ad+bc)\)

无需证明，肉眼化简。

单位复数根

在单位圆上，我们用 \(\omega_{n}^k\) 表示将单位圆 \(n\) 等分，取其第 \(k\) 条线对应的单位复数。其中 \(\omega_n^0=1\) ，逆时针方向编号，如图所示：

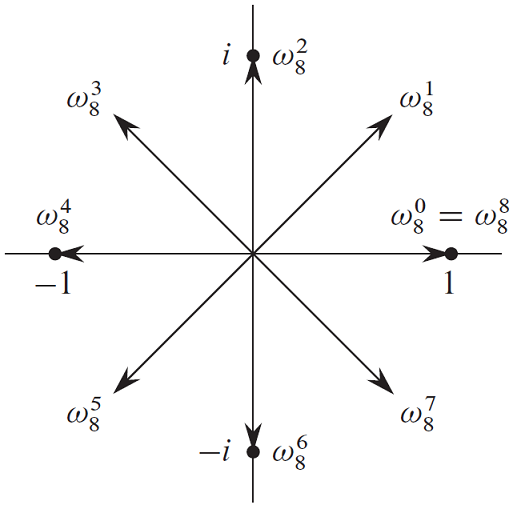
单位复根有一些重要的性质。

消去引理

\(\omega_{dn}^{dk}=\omega_{n}^k\) 其中 \(n,k\geq 0,d>0\)

折半引理

\((\omega_n^{k+n/2})^2=(\omega_n^k)^2\) 其中\(n\geq0,k\geq 0\)

如果借助向量去理解的话，理解起来非常方便。

多项式

一个形如 \(\displaystyle A(x)=\sum_{i=0}^{n-1}a_ix^i\) 的式子。

系数表示

直接列出 \(A(x)\) 的各项系数。这种表示方法可以 \(O(n)\) 的实现多项式加法，但多项式乘法却需要 \(O(n^2)\)

点值表示

通过带入若干个特值确定，显然，一个最高次为 \(n-1\) 的多项式需要 \(n\) 的特殊值便唯一确定。这种表示方法可以 \(O(n)\) 的加和乘，但是要转化成系数表示才能体现出它作为多项式的价值。

DFT

对于一个列向量 \(a=(a_0,a_1,\cdots,a_{n-1})\) ，以它为系数的多项式 \(A(x)=\displaystyle\sum_{j=0}^{n-1}a_jx^j\)

若有一个列向量 \(y=(y_0,y_1,\cdots,y_{n-1})\) 满足 \(y_k=A(\omega_n^k)\) ，则\(y=\text{DFT}_n(a)\)

\(\text{DFT}\) 的全称为离散傅里叶变换，是将多项式的系数表达化作点值表达的一个变换。

同理 \(a=\text{DFT}_n^{-1}(y)\) ，\(\text{DFT}^{-1}\) 就是逆离散傅里叶变换，也称 \(\text{IDFT}\)，我们尝试写出 \(\text{DFT}^{-1}\) 的表达式。

写出 \(y\) 与 \(a\) 的关系

\[y_k=\sum_{j=0}^{n-1}a_j\omega^{kj}
\]

然后我们可以矩阵乘积 \(y=V_na\) 的形式表示向量 \(a\) 到向量 \(y\) 的变换。\(V_n\) 为由 \(\omega_n\) 各项指数构成的范德蒙德矩阵。

\[\begin{pmatrix}
y_0\\
y_1\\
y_2\\
y_3\\
\vdots\\
y_{n-1}\\
\end{pmatrix}
=
\begin{pmatrix}
\omega^0 & \omega^0 &\omega^0 & \omega^0 & \cdots & \omega^0 \\
\omega^0 & \omega^1 &\omega^2 & \omega^3 & \cdots & \omega^{(n-1)}\\
\omega^0 & \omega^2 &\omega^4 & \omega^6 & \cdots & \omega^{2(n-1)} \\
\omega^0 & \omega^3 &\omega^6 & \omega^9 & \cdots & \omega^{3(n-1)} \\
\vdots & \vdots & \vdots & \vdots & \ddots &\vdots\\
\omega^{0} & \omega^{1(n-1)} &\omega^{2(n-1)} & \omega^{3(n-1)} & \cdots & \omega^{(n-1)(n-1)} \\
\end{pmatrix}
\begin{pmatrix}
a_0\\
a_1\\
a_2\\
a_3\\
\vdots\\
a_{n-1}\\
\end{pmatrix}
\]

那我们现在要求的就是 \(V_n^{-1}\) 的矩阵，即 \(V_n\) 的逆矩阵。

有如下定理：

对于 \(j,k\in[0,n)\) ，\(V_n^{-1}\) \((j,k)\) 处的元素为 \(\omega_n^{-jk}/n\)

证明如下

\[\begin{array}{}
[V_nV_n^{-1}]_{jj'}&=\displaystyle\sum_{k=0}\omega_n^{jk}\omega^{-kj'}/n\\
&=\displaystyle{1\over n}\sum_{k=0}\omega_n^{k(j-j')}
\end{array}
\]

显然，当 \(j=j'\) 时，\([V_nV_n^{-1}]_{jj'}\) 的值为 \(1\) ，否则为 \(0\) ，那么 \([V_nV_n^{-1}]\) 是一个行列数为 \(n\) 的单位矩阵，即得证 \(V^{-1}\) 为 \(V\) 的逆矩阵。

那么在作 \(\text{IDFT}\) 的时候，只需将单位根换成 \({\omega_n^{-1}}\) ，最后系数再除以 \(n\) 即可。

当然，直接变换是 \(O(n^2)\) 的。我们考虑用分治的思想进行变换。

FFT

首先观察多项式 \(A(x)\) ，我们将指数分奇偶两类。偶数项以 \(\{a_0,a_2,...,a_{n-2}\}\) 构造一个新的多项式 \(\displaystyle A^{[0]}(x)=\sum_{j=0}^{n/2-1}a_{2j}x^j\)，奇数项同理为 \(\displaystyle A^{[1]}(x)=\sum_{j=0}^{n/2-1}a_{2j+1}x^j\)。

那么显然有

\[A(x)=A^{[0]}(x^2)+xA^{[1]}(x^2)
\]

我们把 \(\omega_n^k\) 代入得到

\[A(\omega_n^k)=A^{[0]}(\omega_n^{2k})+\omega_n^kA^{[1]}(\omega_n^{2k})
\]

利用消去引理得到

\[A(\omega_n^k)=A^{[0]}(\omega_{n/2}^k)+\omega_n^kA^{[1]}(\omega_{n/2}^k)
\]

那么将 \(A^{[0]},A^{[1]}\) 的系数向量 \(a^{[0]},a^{[1]}\) 进行一次 \(\text{DFT}\) ，分别得到 \(y^{[0]},y^{[1]}\) 。

有

\[y^{[0]}_k=A^{[0]}(\omega_{n/2}^k)\\
y^{[1]}_k=A^{[1]}(\omega_{n/2}^k)
\]

只要令 \(k<n/2\) ，将 \(k\geq n/2\) 的部分用折半引理即可。

\[A(\omega_n^k)=A^{[0]}(\omega_{n/2}^k)+\omega_n^kA^{[1]}(\omega_{n/2}^k)\\
A(\omega_n^{k+n/2})=A^{[0]}(\omega_{n/2}^k)-\omega_n^kA^{[1]}(\omega_{n/2}^k)
\]

推导不难，注意将在单位圆上的旋转借用平面向量来理解。

用 \(y\) 代入，最终的表达式为

\[y_k=y^{[0]}_k+\omega_n^ky_k^{[1]}\\
y_{k+n/2}=y_k^{[0]}-\omega_n^ky_k^{[1]}
\]

这样就可以分治求解了。

更高效的FFT

事实上 \(\text{FFT}\) 可以迭代求解。先观察一下递归求解的过程，如图所示。

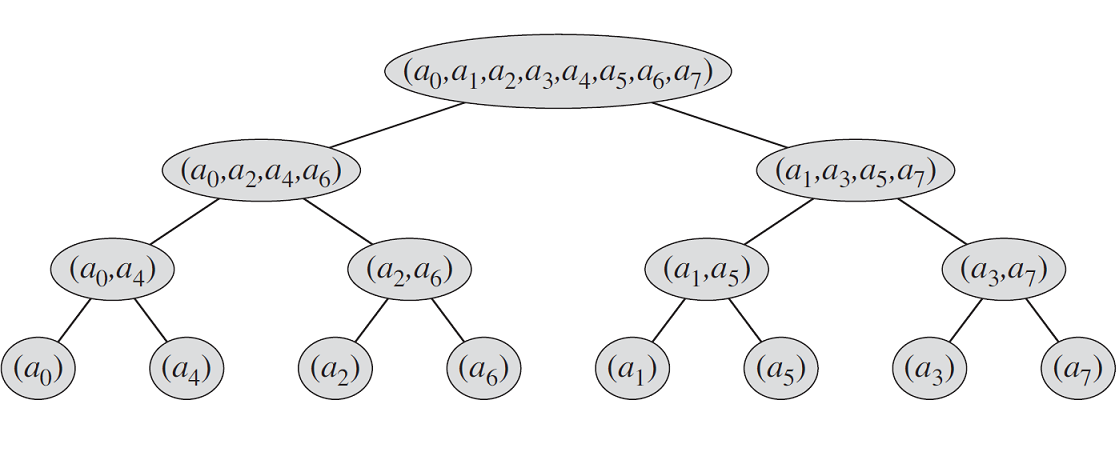
然后用人类智慧观察，发现 \(a_i\) 在底层是在的位置为 \(i\) 的二进制位翻转。

发现只需要枚举区间长度，扫整个序列，就可以进行对区间进行合并。观察递归求解的式子

\[y_k=y^{[0]}_k+\omega_n^ky_k^{[1]}\\
y_{k+n/2}=y_k^{[0]}-\omega_n^ky_k^{[1]}
\]

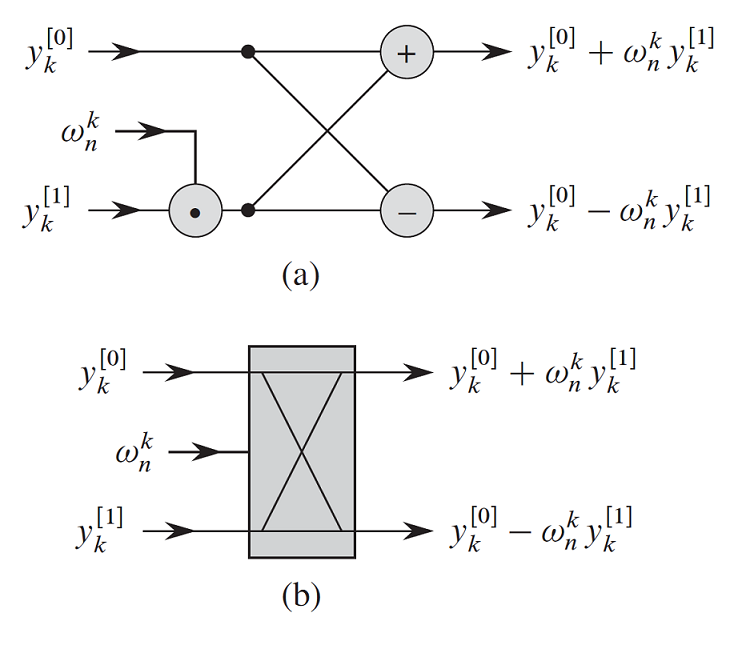
它的流程可以用上图来表示，上面操作叫作蝴蝶操作，其实和递归求解的流程相似。具体还是看代码，码风还是清晰的。

struct Complex
{
	double x,y;
	Complex operator +(const Complex &_){return (Complex){x+_.x,y+_.y};}
	Complex operator -(const Complex &_){return (Complex){x-_.x,y-_.y};}
	Complex operator *(const Complex &_){return (Complex){x*_.x-y*_.y,x*_.y+y*_.x};}
	Complex operator /(const int &_){return (Complex){x/_,y/_};}
};
namespace _Polynomial
{
	Complex A[N<<1],B[N<<1];
	Complex w[N<<1];int r[N<<1];
	void DFT(Complex *a,int op,int n)
	{
		FOR(i,0,n-1)if(i<r[i])swap(a[i],a[r[i]]);	//位翻转
		for(int i=2;i<=n;i<<=1)		//合并出一个长i的区间
			for(int j=0;j<n;j+=i)		//区间开头的位置
				for(int k=0;k<i/2;k++)		//蝴蝶操作
				{
					Complex u=a[j+k],t=w[op==1?n/i*k:n-n/i*k]*a[j+k+i/2];
					a[j+k]=u+t,a[j+k+i/2]=u-t;
				}
		if(op==-1)FOR(i,0,n-1)a[i]=a[i]/n;
	}
	void multiply(const int *a,const int *b,int *c,int n1,int n2)
	{
		int n=1;
		while(n<n1+n2-1)n<<=1;
		FOR(i,0,n1-1)A[i].x=a[i],A[i].y=0;
		FOR(i,0,n2-1)B[i].x=b[i],B[i].y=0;
		FOR(i,n1,n-1)A[i].x=A[i].y=0;
		FOR(i,n2,n-1)B[i].x=B[i].y=0;
		FOR(i,0,n-1)r[i]=(r[i>>1]>>1)|((i&1)*(n>>1));
		FOR(i,0,n)w[i]=(Complex){cos(2*PI*i/n),sin(2*PI*i/n)};

		DFT(A,1,n),DFT(B,1,n);
		FOR(i,0,n-1)A[i]=A[i]*B[i];
		DFT(A,-1,n);
		FOR(i,0,n1+n2-2)c[i]=A[i].x+0.5;
	}
};

显而易见，由于 \(\text{double}\) 的存在，精度多多少少会被卡一点。而具体的题目经常往往会给一个特殊的模数，这种时候就要用到接下来介绍的算法了。

NTT-快速数论变换

待补充。。。