国密 SM2 的非对称加密解密过程

国密 SM2 的非对称加密解密过程

椭圆曲线

椭圆曲线是由一组方程描述的点的集合：

y² = x³ + ax + b 其中 a, b 满足 (4a³ + 27b² ≠ 0)

SM2 定义了一个 sm2p256v1 的椭圆曲线方程

各种参数

BigInteger p = FromHex("FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF");
BigInteger a = FromHex("FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC");
BigInteger b = FromHex("28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93");
BigInteger n = FromHex("FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123");
BigInteger h = BigInteger.One;

Point G coord: (22963146547237050559479531362550074578802567295341616970375194840604139615431, 85132369209828568825618990617112496413088388631904505083283536607588877201568)

公钥，私钥

• 私钥：

可以随机生成一个 BigInteger D，必须符合区间 [1, n - 1]

• 公钥：

私钥 D * G(Point) 得到的一个 Point: Q

隐函数微分 dy/dx = (3x² + a) / (2y)

椭圆曲线密码（Elliptic Curve Cryptography，ECC）的安全性主要基于椭圆曲线离散对数问题（Elliptic Curve Discrete Logarithm Problem，ECDLP）的难度。简单来说，如果知道椭圆曲线上的两个点P和Q，并且知道存在一个整数d，使得dP=Q（这里的乘法表示点的数乘，就是把点P加d次），那么想从P和Q推算出d是几乎不可能的。这就是椭圆曲线离散对数问题。

这个乘法异常的复杂 D * G 就是 D 个 G点相加，2 * G 就是过这个点的切线与椭圆曲线的交点，和 x 轴的对称点，还有有限域的处理，求同余...。

所以也能看出来知道公钥和 G 也很难求出 私钥 D

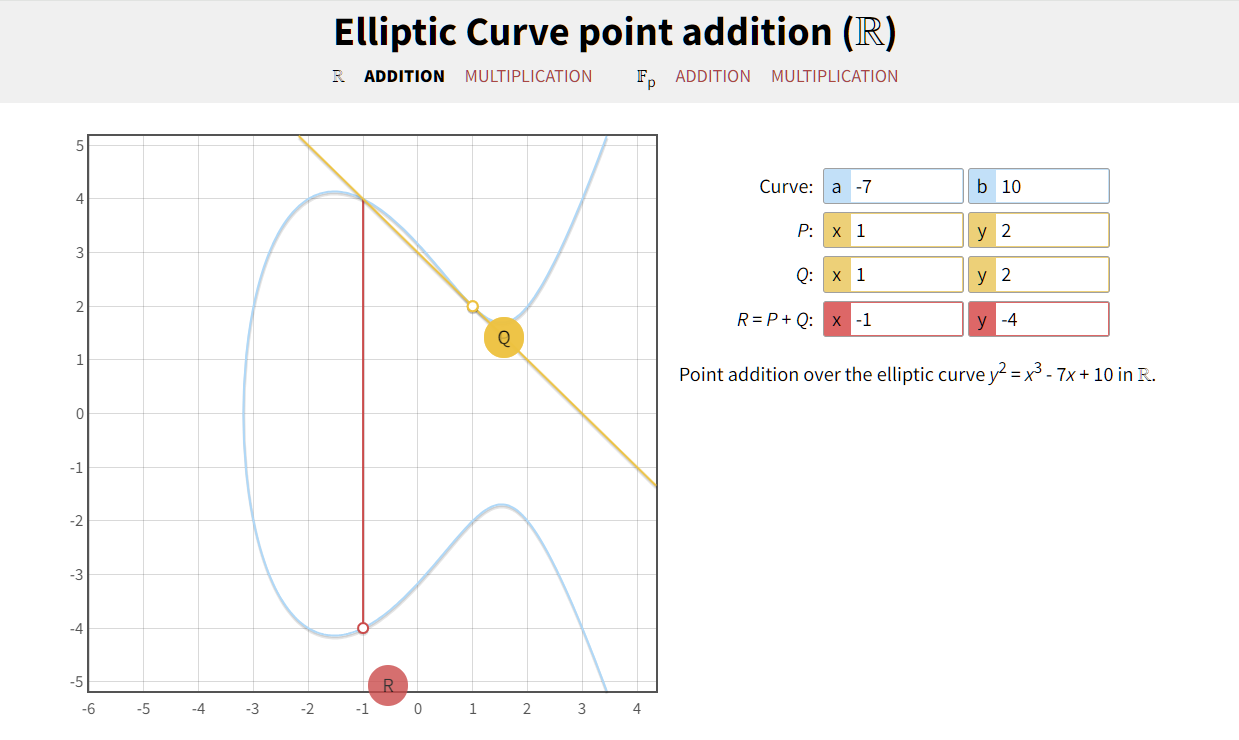
私钥和公钥的关系：

D * G = Q

加密过程

公钥： Q

1. 随机生成一个 BigInteger K
2. K * Q 生成一个 Point(x, y) KPB

C2: 每对原文 byte[] 每32个byte z循环处理，序号初始为1

32 和后续待处理字节长度取小值

1. 对 KPB(x,y), 序号做摘要 记作 buf: byte[32]
2. 这32个字节 分别和 buf的32个字节做异或运算 z[zOff + i] ^= buf[xOff + i];
3. 序号 + 1 处理后续的

C1: k * G

C3: KPB.x 原文byte[], KPB.y 做摘要

解密过程

私钥: D

因为：C1 = K * G

所以 C1 * D = K * G * D = K * (G * D) = K * Q = KPB

然后: 异或运算满足 A ^ B ^ A = B

所以对 C2来相同的运算即可得到原文

C3用来验证是否一致

总结

知道密文和公钥无法解密，因为不知道随机生成的 K

C1 部分的生成和公私钥的生成是一模一样的，类似的原理很难通过 C1 和 G 倒推出K，解不了密

加密后占用空间 C2 和原文长度一致

C1 不压缩 标志位 + x + y = 65, C3 = 摘要长度 32 增大 97

C1 压缩 标志位 + x = 33 C3 = 摘要长度 32 增大 65

然后一般的结果有 C1C2C3 和 C1C3C2两种排列模式

实际情况中，针对这三部分有无数种基于 ASN.1 的包装方式，最终都是按照 C1C2C3 组装好进行解密