最小二乘法的矩阵正则化改进——“岭回归”和“LASSO回归”算法

看代码过程中发现了一个很奇怪的概念，叫做“最小二乘法的矩阵正则化”，这个词汇十分的陌生，虽然最小二乘法是知道的，但是用了矩阵正则化的最小二乘法是个什么东西呢？

相关代码见：

强化学习：连续控制问题中Actor-Critic算法的linear baseline

后来在网上一通查才知道，原来“最小二乘法的二范数矩阵正则化”就是“岭回归”算法，而“最小二乘法的一范数矩阵正则化”就是“LASSO回归”算法。

不得不感慨，为什么有的人写东西总是要挑那些令人生疏的词汇表达，用一些常见的词汇表达不是更易懂嘛。

note: 本文不对“岭回归”和“LASSO回归”算法进行数学推导和数学解释，也不从统计学上给出显著性解释，本文就是解释一下算法概念的别名。

-----------------------------------------------------

给出岭回归的推导公式：

图及代码源自：https://blog.csdn.net/weixin_44831924/article/details/103929256

sklearn对Longley数据集进行岭回归计算：

（数据集见：

https://www.cnblogs.com/devilmaycry812839668/p/17445172.html）

import numpy as np
from numpy import genfromtxt
from sklearn import linear_model
import matplotlib.pyplot as plt

# 读入数据
data = genfromtxt(r"longley.csv",delimiter=',')
print(data)

# 切分数据
x_data = data[1:,2:]
y_data = data[1:,1]
print(x_data)
print(y_data)

# 创建模型
# 生成50个值作为label的候选值，此处是alphas
# linspace默认生成50个值，若想生成100个，可以修改为(0.001,1,100)
alphas_to_test = np.linspace(0.001,1)
# 创建模型，保存误差值，ridge表示岭回归，cv表示交叉验证
model = linear_model.RidgeCV(alphas=alphas_to_test, store_cv_values=True)
model.fit(x_data,y_data)

# 岭系数
print(model.alpha_)
# loss值（16个loss值，50个岭系数，每一个系数对应一个loss值）
print(model.cv_values_.shape)

# 画图，横坐标是岭系数的50个值，纵坐标是交叉验证法得到的16个loss值的平均值
# 岭系数跟loss值的关系
plt.plot(alphas_to_test,model.cv_values_.mean(axis=0))
# 选取的岭系数值的位置
plt.plot(model.alpha_,min(model.cv_values_.mean(axis=0)),'ro')
plt.show()

model.predit(x_data[2,np.newaxis])

----------------------------------------------------------

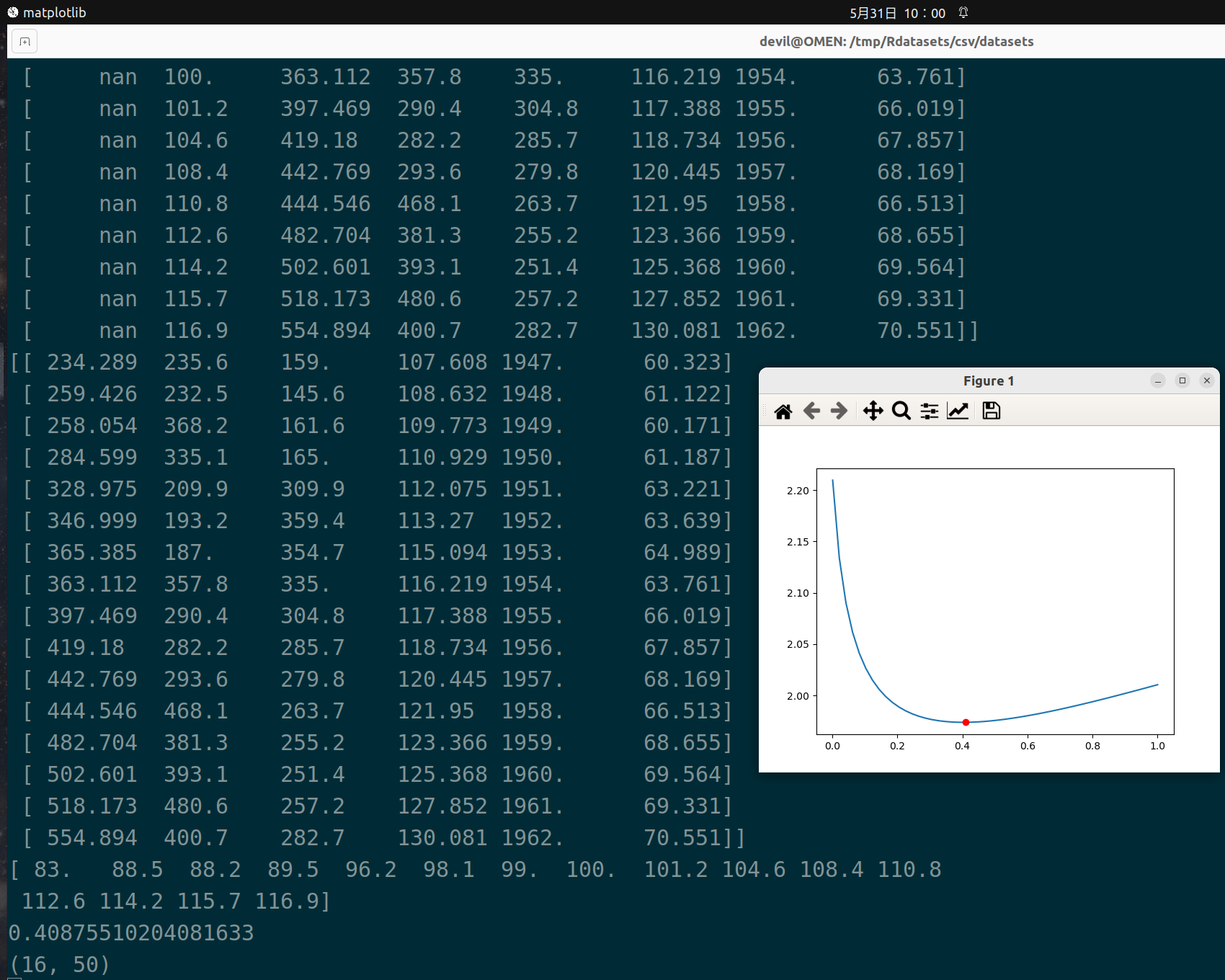
给出一个pytorch的岭回归代码（部分代码，不可运行）：

    def fit(self, episodes):
        # sequence_length * batch_size x feature_size
        featmat = self._feature(episodes).view(-1, self.feature_size)
        # sequence_length * batch_size x 1
        returns = episodes.returns.view(-1, 1)

        reg_coeff = self._reg_coeff
        eye = torch.eye(self.feature_size, dtype=torch.float32,
                        device=self.linear.weight.device)
        for _ in range(5):
            try:
                coeffs = torch.linalg.lstsq(
                    torch.matmul(featmat.t(), featmat) + reg_coeff * eye,
                    torch.matmul(featmat.t(), returns)
                ).solution
                break
            except RuntimeError:
                reg_coeff += 10
        else:
            raise RuntimeError('Unable to solve the normal equations in '
                               '`LinearFeatureBaseline`. The matrix X^T*X (with X the design '
                               'matrix) is not full-rank, regardless of the regularization '
                               '(maximum regularization: {0}).'.format(reg_coeff))
        self.linear.weight.data = coeffs.data.t()

详细代码地址：

https://gitee.com/devilmaycry812839668/MAML-Pytorch-RL/blob/master/maml_rl/baseline.py