算法1：Fibonacci数列

斐波那契数列（Fibonacci）

---

一、背景介绍

斐波那契数列（Fibonacci sequence），又称黄金分割数列，因数学家莱昂纳多·斐波那契（Leonardo Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”。

【兔子繁殖问题】

一般而言，兔子在出生两个月后，就有繁殖能力，一对兔子每个月能生出一对小兔子来。如果所有兔子都不死，那么一年以后可以繁殖多少对兔子？

---

二、数学定义

指的是这样一个数列：0、1、1、2、3、5、8、13、21、34、……

用数学课表示为：

---

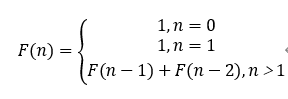
三、核心代码

方法一：递归

第n个Fibonacci数可递归地计算为：

int fibonacci(int n) {
    if (n <= 1)
       return 1;
    return fibonacci(n - 1) + fibonacci(n - 2);
}

方法二：迭代

int fibonacci(int n) {
    if (n <= 1)
        return 1;
    int f = 1, g = 1,ret = 0;
    for (int i = 2; i <= n; i++) {
        ret = f + g;
        f = g;
        g = ret;
    }
    return ret;
}

---

四、时间复杂度分析

方法一：递归

即可得到O(n^2)。

方法二：迭代

第一种解法比较简单，但是多个元素重复计算，因而时间复杂度较高，为了避免重复计算，可进行循环计算减少时间复杂度，降为O(n)。

五、完整代码

方法一：递归

#include<iostream>
#define scanf scanf_s
using namespace std;

int fibonacci(int n) {
    if (n <= 1)
       return 1;
    return fibonacci(n - 1) + fibonacci(n - 2);
}

int main() {
    printf("请输入下标：");
    int n;
    scanf_s("%d", &n);
    printf("下标为%d的fibonacci数为%d\n",n,  fibonacci(n));
    return 0;
}

方法二：迭代

#include<iostream>
#define scanf scanf_s
using namespace std;

int fibonacci(int n) {
    if (n <= 1)
        return 1;
    int f = 1, g = 1,ret = 0;
    for (int i = 2; i <= n; i++) {
        ret = f + g;
        f = g;
        g = ret;
    }
    return ret;
}

int main() {
    printf("请输入下标：");
    int n;
    scanf_s("%d", &n);
    printf("下标为%d的fibonacci数为%d\n",n,  fibonacci(n));
    return 0;
}

---

六、提升设计

因而计算f(n)就简化为了计算矩阵的(n-2)次方，而计算矩阵的(n-2)次方，我们又可以进行分解，即计算矩阵(n-2)/2次方的平方，逐步分解下去，由于折半计算矩阵次方，因而时间复杂度为O(log n) 。

#include<iostream>
using namespace std;

class Matrix {
public:
	int n;
	int** m;
	Matrix(int num) {
		m = new int* [num];
		for (int i = 0; i < num; i++) {
			m[i] = new int[num];
		}
		n = num;
		clear();
	}
	void clear() {
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < n; j++) {
				m[i][j] = 0;
			}
		}
	}
	void unit() {
		clear();
		for (int i = 0; i < n; i++) {
			m[i][i] = 1;
		}
	}
	Matrix operator=(const Matrix mtx) {
		Matrix(mtx.n);
		for (int i = 0; i < mtx.n; ++i) {
			for (int j = 0; j < mtx.n; ++j) {
				m[i][j] = mtx.m[i][j];
			}
		}
		return *this;
	}
	Matrix operator*(const Matrix& mtx) {
		Matrix result(mtx.n);
		result.clear();
		for (int i = 0; i < mtx.n; ++i) {
			for (int j = 0; j < mtx.n; ++j) {
				for (int k = 0; k < mtx.n; ++k) {
					result.m[i][j] += m[i][k] * mtx.m[k][j];
				}
			}
		}
		return result;
	}
};

int main(int argc,const char*argv[]) {
	unsigned int num = 2;
	Matrix first(num);
	first.m[0][0] = 1;
	first.m[0][1] = 1;
	first.m[1][0] = 1;
	first.m[1][1] = 0;
	int t;
	cout << "请输入下标： ";
	cin >> t;
	Matrix result(num);
	result.unit();
	int n = t - 2;
	while (n) {
		if (n % 2) {
			result = result * first;
		}
		first = first * first;
		n = n / 2;
	}
	cout << (result.m[0][0] + result.m[0][1]) << endl;
	return 0;
}