pytorch 反向梯度计算问题
计算如下
\begin{array}{l}{x_{1}=w_{1} * \text { input }} \\ {x_{2}=w_{2} * x_{1}} \\ {x_{3}=w_{3} * x_{2}}\end{array}
其中$w_{1}$，$w_{2}$，$w_{3}$是权重参数，是需要梯度的。在初始化时，三个值分别为1，0，1。
程序代码如下：
import torch
import torch.nn as nn input_data = torch.randn(1) weight1 = torch.ones(1,requires_grad=True)
weight2 = torch.zeros(1,requires_grad=True)
weight3 = torch.ones(1,requires_grad=True) x_1 = weight1 * input_data
x_2 = weight2 * x_1
x_3 = weight3 * x_2 one = torch.ones(1)
x_3 = x_3 * one
x_3.backward() print("x1:{},x2{},x3{},weight1_gard:{},weight2_gard:{},weight3_gard:{}".format(x_1,x_2,x_3,
weight1.grad,weight2.grad,weight3.grad))
运行时，随机产生的Input_data为1.688，三个权重的梯度值分别为0，1.688，0。
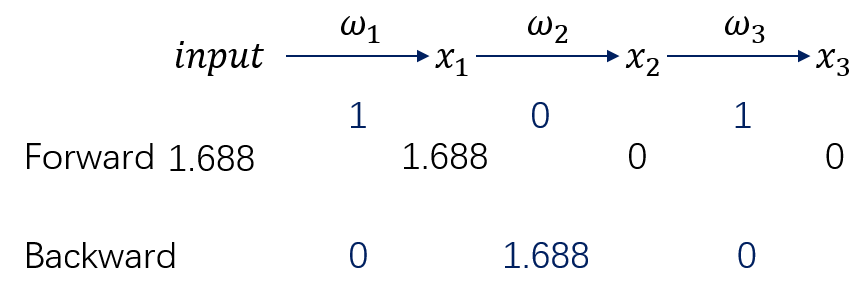
梯度的计算公式如下：
\begin{equation}
\frac{\partial x_{3}}{\partial w_{3}}=x_{2}
\end{equation}
\begin{equation}
\frac{\partial x_{3}}{\partial x_{2}}=w_{3}
\end{equation}
\begin{equation}
\frac{\partial x_{3}}{\partial w_{2}}=\frac{\partial x_{3}}{\partial x_{2}} \frac{\partial x_{2}}{\partial w_{2}}=w_{3} * x_{1}
\end{equation}
\begin{equation}
\frac{\partial x_{3}}{\partial x_{1}}=\frac{\partial x_{3}}{\partial x_{2}} \frac{\partial x_{2}}{\partial x_{1}}=w_{3} * w_{2}
\end{equation}
\begin{equation}
\frac{\partial x_{3}}{\partial w_{1}}=\frac{\partial x_{3}}{\partial x_{1}} \frac{\partial x_{1}}{\partial w_{1}}=w_{3} * w_{2} * input
\end{equation}
由此可以看出一个问题是，权重数据为0，不代表其梯度也会等于0，权重数据不为0，不代表其梯度就不会为0.
在进行一些模型修改的时候常常会将一些卷积核置为零，但是如果这些卷积核仍然requires_grad=True，那么在反向梯度传播的时候这些卷积核还是有可能会更新改变值的。
下面分析一段程序：
class Net(nn.Module):
def __init__(self):
super(Net,self).__init__()
self.conv1 = nn.Conv2d(3,3,kernel_size=2,padding=1,bias=False)
self.conv2 = nn.Conv2d(3,3,kernel_size=2,padding=1,bias=False) def forward(self,x):
x = self.conv1(x)
print("x(1):",x)
x = self.conv2(x)
print("x(2):",x) x = x.view(x.shape[0],-1)
x = torch.sum(x,dim=1)
return x mask = torch.tensor([1.0,0.0,1.0]) model = Net() for name,weight in model.named_parameters():
weight.data = weight.data.transpose(0,3) * mask #注意此处是将输出的channels数目和最后一个维度进行对调
weight.data = weight.data.transpose(0,3)
break input_data = torch.randn(1,3,4,4)
model.train()
out = model(input_data)
print(out)
out.backward() for name,weight in model.named_parameters():
print("weight:",weight)
print("weight.grad:",weight.grad)
这段代码想通过将权重值置为0的形式实现上图中的卷积核选择，结果如下，主要关注于卷积核的梯度值：
tensor([-5.7640], grad_fn=<SumBackward2>)
weight: Parameter containing:
tensor([[[[ 0.0543, -0.1514],
[ 0.1190, -0.1161]], [[-0.0760, -0.1224],
[-0.1884, 0.1472]], [[-0.1482, 0.0413],
[ 0.0735, -0.2729]]], [[[-0.0000, 0.0000],
[ 0.0000, -0.0000]], [[-0.0000, 0.0000],
[-0.0000, -0.0000]], [[ 0.0000, 0.0000],
[-0.0000, 0.0000]]], [[[ 0.1193, 0.0289],
[ 0.1296, 0.2184]], [[-0.2156, -0.0562],
[ 0.1257, 0.2109]], [[ 0.2618, 0.1946],
[-0.2667, 0.1019]]]], requires_grad=True)
weight.grad: tensor([[[[ 1.3665, 1.3665],
[ 1.3665, 1.3665]], [[-0.1851, -0.1851],
[-0.1851, -0.1851]], [[ 0.8171, 0.8171],
[ 0.8171, 0.8171]]], [[[-1.3336, -1.3336],
[-1.3336, -1.3336]], [[ 0.1807, 0.1807],
[ 0.1807, 0.1807]], [[-0.7974, -0.7974],
[-0.7974, -0.7974]]], [[[-8.2042, -8.2042],
[-8.2042, -8.2042]], [[ 1.1116, 1.1116],
[ 1.1116, 1.1116]], [[-4.9058, -4.9058],
[-4.9058, -4.9058]]]])
weight: Parameter containing:
tensor([[[[ 0.1661, -0.2404],
[-0.2504, 0.0886]], [[-0.1079, 0.2199],
[ 0.0405, -0.2834]], [[-0.1478, -0.1596],
[ 0.0747, -0.0178]]], [[[ 0.2699, 0.0623],
[-0.0816, 0.1588]], [[ 0.0798, -0.1606],
[-0.2531, 0.2330]], [[-0.1956, 0.1329],
[ 0.1160, -0.0881]]], [[[ 0.0497, 0.0830],
[ 0.0780, -0.1898]], [[ 0.1204, -0.0770],
[ 0.0008, -0.0018]], [[-0.2224, -0.2384],
[-0.1398, -0.2800]]]], requires_grad=True)
weight.grad: tensor([[[[-1.7231, -1.7231],
[-1.7231, -1.7231]], [[ 0.0000, 0.0000],
[ 0.0000, 0.0000]], [[ 4.6560, 4.6560],
[ 4.6560, 4.6560]]], [[[-1.7231, -1.7231],
[-1.7231, -1.7231]], [[ 0.0000, 0.0000],
[ 0.0000, 0.0000]], [[ 4.6560, 4.6560],
[ 4.6560, 4.6560]]], [[[-1.7231, -1.7231],
[-1.7231, -1.7231]], [[ 0.0000, 0.0000],
[ 0.0000, 0.0000]], [[ 4.6560, 4.6560],
[ 4.6560, 4.6560]]]])
这样梯度值还是在更新的。
另外一种mask的选择的方式，程序如下：
class Net(nn.Module):
def __init__(self):
super(Net,self).__init__()
self.conv1 = nn.Conv2d(3,3,kernel_size=3,padding=1,bias=False)
self.mask = torch.tensor([1.0,0.0,1.0])
self.conv2 = nn.Conv2d(3,3,kernel_size=3,padding=1,bias=False) def forward(self,x):
x = self.conv1(x)
x = x.transpose(1,3) # 此处的是将channels的维度和最后一个维度对调
x = self.mask * x
x = x.transpose(1,3)
x = self.conv2(x) x = x.view(x.shape[0],-1)
x = torch.sum(x,dim=1)
return x model = Net() input_data = torch.randn(1,3,4,4)
model.train()
out = model(input_data)
print(out)
out.backward() for name,weight in model.named_parameters():
print("weight:",weight)
print("weight.grad:",weight.grad)
结果如下：
tensor([0.2569], grad_fn=<SumBackward2>)
weight: Parameter containing:
tensor([[[[-0.0880, -0.1685, -0.0367],
[-0.0882, 0.0551, -0.0204],
[-0.0213, 0.1404, 0.1892]], [[ 0.0056, 0.1266, 0.0108],
[-0.1146, 0.1275, 0.1070],
[-0.1756, -0.1015, 0.1670]], [[ 0.1145, 0.0617, 0.0290],
[ 0.0034, -0.0688, -0.0720],
[-0.1227, -0.1408, -0.0095]]], [[[ 0.1335, -0.1492, -0.0962],
[-0.1691, -0.1726, 0.1218],
[ 0.1924, 0.0165, 0.1454]], [[-0.1302, -0.1700, 0.1157],
[ 0.0050, -0.0149, -0.0506],
[-0.0059, 0.0439, 0.1396]], [[-0.0524, 0.0682, -0.0892],
[-0.1708, -0.0117, -0.0379],
[-0.0459, 0.0743, -0.0160]]], [[[ 0.1923, 0.0397, -0.1278],
[-0.0590, -0.1523, 0.1832],
[ 0.0136, -0.0047, 0.1030]], [[ 0.1912, 0.1178, -0.0915],
[ 0.0639, -0.0495, -0.0504],
[-0.1025, 0.0448, -0.1506]], [[ 0.0784, 0.0163, 0.0904],
[ 0.1349, -0.0998, -0.0801],
[ 0.1837, -0.1003, -0.1355]]]], requires_grad=True)
weight.grad: tensor([[[[ 1.2873, 2.1295, 1.7824],
[ 1.8223, 2.5102, 1.4646],
[ 1.0475, 1.5060, 0.7760]], [[ 0.3358, 1.0468, 0.7017],
[ 1.2767, 3.0948, 2.3152],
[ 1.5075, 3.1297, 2.0517]], [[-0.1350, -0.0052, 0.5159],
[-0.5552, -0.2897, -0.2935],
[-0.8585, -0.3860, -0.6307]]], [[[ 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000]], [[ 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000]], [[ 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000]]], [[[-0.5196, -0.5230, -1.4080],
[-1.0556, -1.3059, -1.9042],
[-0.9298, -1.3619, -0.9315]], [[-0.1840, -0.3386, -0.1826],
[-0.4814, -0.6702, -1.3245],
[-0.6749, -0.9496, -1.7621]], [[-0.5977, -0.0242, -0.8976],
[-0.7431, -0.0033, -0.8301],
[-0.5861, 0.1346, -0.1433]]]])
weight: Parameter containing:
tensor([[[[-0.1239, 0.1291, 0.1867],
[-0.1434, 0.1218, 0.0452],
[ 0.0722, 0.0830, -0.1149]], [[-0.0145, -0.1000, -0.0537],
[ 0.1225, -0.0513, -0.0325],
[-0.0796, -0.1129, 0.0850]], [[-0.0283, -0.0441, 0.0508],
[ 0.0523, -0.1224, 0.0353],
[ 0.1726, 0.0695, 0.0078]]], [[[ 0.0371, 0.1536, -0.0583],
[ 0.0471, 0.0636, 0.1264],
[-0.0544, 0.1420, 0.0421]], [[-0.1213, 0.1672, -0.0086],
[ 0.1251, -0.1603, -0.0988],
[ 0.1399, -0.0367, -0.1656]], [[ 0.0279, -0.1697, 0.0959],
[-0.1719, -0.0208, 0.0677],
[-0.1116, -0.0659, 0.1343]]], [[[-0.0840, -0.0361, -0.1864],
[ 0.1757, 0.1003, -0.0931],
[-0.1388, -0.0980, -0.0236]], [[ 0.0761, 0.0710, -0.1916],
[ 0.0159, 0.1678, -0.1378],
[ 0.1372, -0.1410, -0.0596]], [[-0.1344, 0.0832, 0.0147],
[ 0.0531, -0.1044, 0.0755],
[-0.1519, 0.1288, -0.1672]]]], requires_grad=True)
weight.grad: tensor([[[[ 0.3392, 0.4461, -0.4528],
[ 0.6036, 0.7465, -0.0223],
[ 1.0414, 0.8226, -0.3322]], [[ 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000]], [[ 0.4305, -0.6932, -0.6299],
[ 0.4147, -0.5902, -0.2296],
[-0.0378, -0.8272, -0.2457]]], [[[ 0.3392, 0.4461, -0.4528],
[ 0.6036, 0.7465, -0.0223],
[ 1.0414, 0.8226, -0.3322]], [[ 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000]], [[ 0.4305, -0.6932, -0.6299],
[ 0.4147, -0.5902, -0.2296],
[-0.0378, -0.8272, -0.2457]]], [[[ 0.3392, 0.4461, -0.4528],
[ 0.6036, 0.7465, -0.0223],
[ 1.0414, 0.8226, -0.3322]], [[ 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000]], [[ 0.4305, -0.6932, -0.6299],
[ 0.4147, -0.5902, -0.2296],
[-0.0378, -0.8272, -0.2457]]]])
——————————————————————————————————————————————————————————————————————————————————————————————————————————————————
为什么会有这种不同呢？这个与反向梯度传播的计算有关系，对于权重的梯度的计算，在链式求导法则当中其实与中间节点的值并没有什么关系，反而与权重之前的节点值有关系，如果有疑问可以画个图分析一下。
pytorch 反向梯度计算问题的更多相关文章
- [图解tensorflow源码] MatMul 矩阵乘积运算 （前向计算，反向梯度计算）
- [tensorflow源码分析] Conv2d卷积运算 （前向计算，反向梯度计算）
- 使用PyTorch构建神经网络以及反向传播计算
使用PyTorch构建神经网络以及反向传播计算 前一段时间南京出现了疫情,大概原因是因为境外飞机清洁处理不恰当,导致清理人员感染.话说国外一天不消停,国内就得一直严防死守.沈阳出现了一例感染人员,我在 ...
- 实现属于自己的TensorFlow(二) - 梯度计算与反向传播
前言 上一篇中介绍了计算图以及前向传播的实现,本文中将主要介绍对于模型优化非常重要的反向传播算法以及反向传播算法中梯度计算的实现.因为在计算梯度的时候需要涉及到矩阵梯度的计算,本文针对几种常用操作的梯 ...
- Softmax 损失-梯度计算
本文介绍Softmax运算.Softmax损失函数及其反向传播梯度计算, 内容上承接前两篇博文 损失函数 & 手推反向传播公式. Softmax 梯度 设有K类, 那么期望标签y形如\([0, ...
- PyTorch 实战：计算 Wasserstein 距离
PyTorch 实战:计算 Wasserstein 距离 2019-09-23 18:42:56 This blog is copied from: https://mp.weixin.qq.com/ ...
- 《神经网络的梯度推导与代码验证》之CNN的前向传播和反向梯度推导
在FNN(DNN)的前向传播,反向梯度推导以及代码验证中,我们不仅总结了FNN(DNN)这种神经网络结构的前向传播和反向梯度求导公式,还通过tensorflow的自动求微分工具验证了其准确性.在本篇章 ...
- 《神经网络的梯度推导与代码验证》之vanilla RNN的前向传播和反向梯度推导
在本篇章,我们将专门针对vanilla RNN,也就是所谓的原始RNN这种网络结构进行前向传播介绍和反向梯度推导.更多相关内容请见<神经网络的梯度推导与代码验证>系列介绍. 注意: 本系列 ...
- 《神经网络的梯度推导与代码验证》之LSTM的前向传播和反向梯度推导
前言 在本篇章,我们将专门针对LSTM这种网络结构进行前向传播介绍和反向梯度推导. 关于LSTM的梯度推导,这一块确实挺不好掌握,原因有: 一些经典的deep learning 教程,例如花书缺乏相关 ...
随机推荐
- CSAPP阅读笔记-gcc常用参数初探-来自第三章3.2的笔记-P113
gcc是一种C编译器,这次我们根据书上的代码尝试着使用它. 使用之前,先补充前置知识.编译器将源代码转换为可执行代码的流程:首先,预处理器对源代码进行处理,将#define指定的宏进行替换,将#inc ...
- nginx 模块介绍
nginx模块在编译文件下的odjs目录下 cat 查看ngx_modules.c文件 可以看到一些基本extern模块 常用标准模块 1. 性能相关配置 worker_processes numbe ...
- Oracle命令整理
1 常用命令 常用命令 1 sqlplus scott/tiger@192.168.47.10:1521/orcl 后面不要加: sqlplus sys/oracle as sysdb ...
- 02-使用注解配置spring
1 准备工作 1.导包 4+2+spring-aop[新版本需要导入 spring-aop 包] 2.为主配置文件引入新的命名空间(约束) [context] 3.开启使用注解代理配置文件 4.在类中 ...
- Best HTTP
http://blog.csdn.net/u012322710/article/details/52860747 Best HTTP (Pro) 这是一款很多公司都在用的网页插件,感觉确实不错,分P ...
- 坐标深圳 | Kubernetes！我要用这样的姿势拥抱你
欢迎大家前往腾讯云+社区,获取更多腾讯海量技术实践干货哦~ 从去年至今,容器.Kubernetes话题的热度就持续不减,有人说基于容器 +Kubernetes 的新型 PaaS 将会成为云计算的主流: ...
- 腾讯毛华：智能交互，AI助力下的新生态
欢迎大家前往腾讯云+社区,获取更多腾讯海量技术实践干货哦~ 演讲人:毛华 腾讯云语音云总经理 背景:5月23-24日,以"焕启"为主题的腾讯"云+未来"峰会在广 ...
- VRRP协议介绍--转
http://www.cnblogs.com/jony413/articles/2697404.html VRRP协议介绍 参考资料: RFC 3768 1. 前言 VRRP(Virtual Rout ...
- Whu 1603——Minimum Sum——————【单个元素贡献、滑窗】
Problem 1603 - Minimum Sum Time Limit: 2000MS Memory Limit: 65536KB Total Submit: 623 Accepted: ...
- bzoj 5314: [Jsoi2018]潜入行动
Description 外星人又双叒叕要攻打地球了,外星母舰已经向地球航行!这一次,JYY已经联系好了黄金舰队,打算联合所有JSO Ier抵御外星人的进攻.在黄金舰队就位之前,JYY打算事先了解外星人 ...