【BZOJ2226】[Spoj 5971] LCMSum 莫比乌斯反演（欧拉函数？）

【BZOJ2226】[Spoj 5971] LCMSum

Description

Given n, calculate the sum LCM(1,n) + LCM(2,n) + .. + LCM(n,n), where LCM(i,n) denotes the Least Common Multiple of the integers i and n.

Input

The first line contains T the number of test cases. Each of the next T lines contain an integer n.

Output

Output T lines, one for each test case, containing the required sum.

Sample Input

3
1
2
5

Sample Output

1
4
55

HINT

Constraints
1 <= T <= 300000
1 <= n <= 1000000

题解：好吧我naive了，别人都用欧拉函数就我用莫比乌斯反演，还是写一发吧~

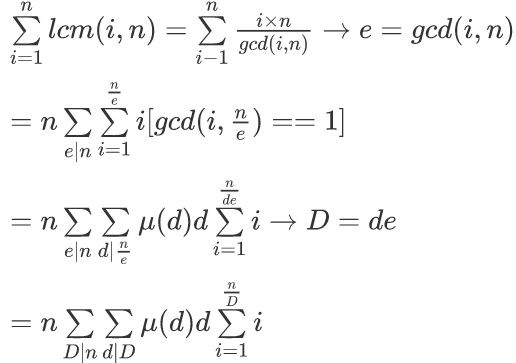
然后线性筛∑μ(d)d，然后O(nlogn)枚举n的约数就行了

>欧拉函数做法

#include <cstdio>
#include <cstring>
#include <iostream>
#include <vector>
using namespace std;
const int m=1000000;
typedef long long ll;
int n,T,num,tot;
int pri[m/10],to[m*14],next[m*14],head[m+10];
bool np[m+10];
vector<int> v[m+10];
ll sm[m+10],ans;
int main()
{
	int i,j;
	for(i=1;i<=m;i++)	for(j=i;j<=m;j+=i)	to[++tot]=i,next[tot]=head[j],head[j]=tot;
	sm[1]=1;
	for(i=2;i<=m;i++)
	{
		if(!np[i])	pri[++num]=i,sm[i]=1-i;
		for(j=1;j<=num&&i*pri[j]<=m;j++)
		{
			np[i*pri[j]]=1;
			if(i%pri[j]==0)
			{
				sm[i*pri[j]]=sm[i];
				break;
			}
			sm[i*pri[j]]=sm[i]*(1ll-pri[j]);
		}
	}
	scanf("%d",&T);
	while(T--)
	{
		scanf("%d",&n),ans=0;
		for(i=head[n];i;i=next[i])	ans+=sm[n/to[i]]*to[i]*(to[i]+1)>>1;
		printf("%lld\n",ans*n);
	}
	return 0;
}