浅谈RBF函数
所谓径向基函数 (Radial Basis Function 简称 RBF), 就是某种沿径向对称的标量函数。 通常定义为空间中任一点x到某一中心xc之间欧氏距离的单调函数 , 可记作 k(||x-xc||), 其作用往往是局部的 , 即当x远离xc时函数取值很小。
最常用的径向基函数是高斯核函数 ,形式为 k(||x-xc||)=exp{- ||x-xc||^2/(2*σ)^2) } 其中xc为核函数中心,σ为函数的宽度参数 , 控制了函数的径向作用范围。
建议首选RBF核函数,因为:
- 能够实现非线性映射;( 线性核函数可以证明是他的一个特例;SIGMOID核函数在某些参数上近似RBF的功能。)
- 参数的数量影响模型的复杂程度,多项式核函数参数较多。
- the RBF kernel has less numerical difficulties.
———–那么,还记得为何要选用核函数么?———–
如果提供的样本线性不可分,结果很简单,线性分类器的求解程序会无限循环,永远也解不出来。这必然使得它的适用范围大大缩小,而它的很多优点我们实在不原意放弃,怎么办呢?是否有某种方法,让线性不可分的数据变得线性可分呢?
例子是下面这张图:
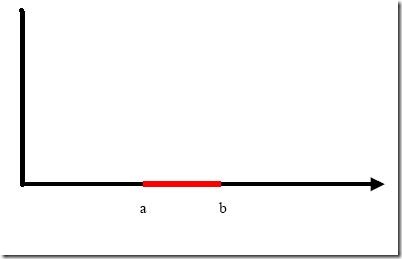
我们把横轴上端点a和b之间红色部分里的所有点定为正类,两边的黑色部分里的点定为负类。试问能找到一个线性函数把两类正确分开么?不能,因为二维空间里的线性函数就是指直线,显然找不到符合条件的直线。
但我们可以找到一条曲线,例如下面这一条:
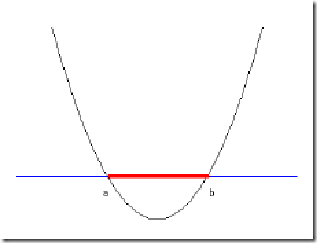
显然通过点在这条曲线的上方还是下方就可以判断点所属的类别(你在横轴上随便找一点,算算这一点的函数值,会发现负类的点函数值一定比0大,而正类的一定比0小)。这条曲线就是我们熟知的二次曲线,它的函数表达式可以写为:
问题只是它不是一个线性函数,但是,下面要注意看了,新建一个向量y和a:
这样g(x)就可以转化为f(y)=<a,y>,你可以把y和a分别回带一下,看看等不等于原来的g(x)。用内积的形式写你可能看不太清楚,实际上f(y)的形式就是:
g(x)=f(y)=ay
在任意维度的空间中,这种形式的函数都是一个线性函数(只不过其中的a和y都是多维向量罢了),因为自变量y的次数不大于1。
看出妙在哪了么?原来在二维空间中一个线性不可分的问题,映射到四维空间后,变成了线性可分的
!因此这也形成了我们最初想解决线性不可分问题的基本思路——向高维空间转化,使其变得线性可分。
而转化最关键的部分就在于找到x到y的映射方法。遗憾的是,如何找到这个映射,没有系统性的方法(也就是说,纯靠猜和凑)。具体到我们的文本分类问题,文本被表示为上千维的向量,即使维数已经如此之高,也常常是线性不可分的,还要向更高的空间转化。其中的难度可想而知。
小Tips:为什么说f(y)=ay是四维空间里的函数?
大家可能一时没看明白。回想一下我们二维空间里的函数定义
g(x)=ax+b
变量x是一维的,为什么说它是二维空间里的函数呢?因为还有一个变量我们没写出来,它的完整形式其实是
y=g(x)=ax+b
即
y=ax+b
看看,有几个变量?两个,二维。
再看看
f(y)=ay
里面的y是三维的变量,再加上f(y)成为四维的了。
用一个具体文本分类的例子来看看这种向高维空间映射从而分类的方法如何运作,想象一下,我们文本分类问题的原始空间是1000维的(即每个要被分类的文档被表示为一个1000维的向量),在这个维度上问题是线性不可分的。现在我们有一个2000维空间里的线性函数
f(x’)=<w’,x’>+b
注意向量的右上角有个 ’哦。它能够将原问题变得可分。式中的 w’和x’都是2000维的向量,只不过w’是定值,而x’是变量(好吧,严格说来这个函数是2001维的,哈哈),现在我们的输入呢,是一个1000维的向量x,分类的过程是先把x变换为2000维的向量x’,然后求这个变换后的向量x’与向量w’的内积,再把这个内积的值和b相加,就得到了结果,看结果大于阈值还是小于阈值就得到了分类结果。
你发现了什么?我们其实只关心那个高维空间里内积的值,那个值算出来了,分类结果就算出来了。而从理论上说, x’是经由x变换来的,因此广义上可以把它叫做x的函数(有一个x,就确定了一个x’,对吧,确定不出第二个),而w’是常量,它是一个低维空间里的常量w经过变换得到的,所以给了一个w 和x的值,就有一个确定的f(x’)值与其对应。这让我们幻想,是否能有这样一种函数K(w,x),他接受低维空间的输入值,却能算出高维空间的内积值<w’,x’>?
如果有这样的函数,那么当给了一个低维空间的输入x以后,
g(x)=K(w,x)+b
f(x’)=<w’,x’>+b
这两个函数的计算结果就完全一样,我们也就用不着费力找那个映射关系,直接拿低维的输入往g(x)里面代就可以了(再次提醒,这回的g(x)就不是线性函数啦,因为你不能保证K(w,x)这个表达式里的x次数不高于1哦)。
万幸的是,这样的K(w,x)确实存在(发现凡是我们人类能解决的问题,大都是巧得不能再巧,特殊得不能再特殊的问题,总是恰好有些能投机取巧的地方才能解决,由此感到人类的渺小),它被称作核函数(核,kernel),而且还不止一个,事实上,只要是满足了Mercer条件的函数,都可以作为核函数。核函数的基本作用就是接受两个低维空间里的向量,能够计算出经过某个变换后在高维空间里的向量内积值。几个比较常用的核函数,俄,教课书里都列过,我就不敲了(懒!)。
回想我们上节说的求一个线性分类器,它的形式应该是:
现在这个就是高维空间里的线性函数(为了区别低维和高维空间里的函数和向量,我改了函数的名字,并且给w和x都加上了 ’),我们就可以用一个低维空间里的函数(再一次的,这个低维空间里的函数就不再是线性的啦)来代替,
又发现什么了?f(x’) 和g(x)里的α,y,b全都是一样一样的!这就是说,尽管给的问题是线性不可分的,但是我们就硬当它是线性问题来求解,只不过求解过程中,凡是要求内积 的时候就用你选定的核函数来算。这样求出来的α再和你选定的核函数一组合,就得到分类器啦!
明白了以上这些,会自然的问接下来两个问题:
1. 既然有很多的核函数,针对具体问题该怎么选择?
2. 如果使用核函数向高维空间映射后,问题仍然是线性不可分的,那怎么办?
第一个问题现在就可以回答你:对核函数的选择,现在还缺乏指导原则!各种实验的观察结果(不光是文本分类)的确表明,某些问题用某些核函数效果很 好,用另一些就很差,但是一般来讲,径向基核函数是不会出太大偏差的一种,首选。
对第二个问题的解决则引出了我们下一节的主题:松弛变量。
核函数有很多种,如线性核、多项式核、Sigmoid 核和 RBF(Radial Basis function)核。本文选定 RBF 核为 SVM 的核函数(RBF 核K(x, y) = exp(-γ || x -y ||的平方),γ > 0)。因为RBF 核可以将样本映射到一个更高维的空间,可以处理当类标签(Class Labels)和特征之间的关系是非线性时的样例。Keerthi 等证明了一个有惩罚参数C 的线性核同有参数(C,γ )(其中C 为惩罚因子,γ 为核参数)的 RBF 核具有相同的性能。对某些参数,Sigmoid核同 RBF 核具有相似的性能[26]。另外,RBF 核与多项式核相比具有参数少的优点。因为参数的个数直接影响到模型选择的复杂性。非常重要的一点是0< Kij ≤1与多项式核相反,核值可能趋向无限(γxi xj + r >1)或者0 < γxi xj + r <1,跨度非常大。而且,必须注意的是Sigmoid 核在某些参数下是不正确的(例如,没有两个向量的内积)。
用交叉验证找到最好的参数 C 和γ 。使用 RBF 核时,要考虑两个参数 C 和γ 。因为参数的选择并没有一定的先验知识,必须做某种类型的模型选择(参数搜索)。目的是确定好的(C,γ)使得分类器能正确的预测未知数据(即测试集数 据),有较高的分类精确率。值得注意的是得到高的训练正确率即是分类器预测类标签已知的训练数据的正确率)不能保证在测试集上具有高的预测精度。因此,通 常采用交叉验证方法提高预测精度。k 折交叉验证(k-fold cross validation)
浅谈RBF函数的更多相关文章
- 浅谈javascript函数节流
浅谈javascript函数节流 什么是函数节流? 函数节流简单的来说就是不想让该函数在很短的时间内连续被调用,比如我们最常见的是窗口缩放的时候,经常会执行一些其他的操作函数,比如发一个ajax请求等 ...
- 开发技术--浅谈Python函数
开发|浅谈Python函数 函数在实际使用中有很多不一样的小九九,我将从最基础的函数内容,延伸出函数的高级用法.此文非科普片~~ 前言 目前所有的文章思想格式都是:知识+情感. 知识:对于所有的知识点 ...
- [转载]浅谈JavaScript函数重载
原文地址:浅谈JavaScript函数重载 作者:ChessZhang 上个星期四下午,接到了网易的视频面试(前端实习生第二轮技术面试).面了一个多小时,自我感觉面试得很糟糕的,因为问到的很多问题都 ...
- 浅谈箭头函数和setTimeout中的this
箭头函数会改变this的指向,这个大家看文档都看到过,可是有没有具体理解呢?我发现自己应该可能大概是......emmmm,然后我整理了一遍,加强一下概念吧顺带再讲一下setTimeout这个函数改写 ...
- [转]浅谈javascript函数劫持
转自:Ph4nt0m Security Team 这么多年了,现在学习依然还是有很多收货,向前辈致敬.转载一方面是自己存档一份,另一方面是让更多喜欢安全的人一同学习. ================ ...
- 浅谈setTimeout函数和setInterval函数
前几天学了js,看到了两个非常有趣的函数,他们分别是setTimeout函数和setInterval函数,这两个函数能使网页呈现非常一些网页中比较常见的效果,比如说图片轮播,等一些非常好玩的效果.下面 ...
- 【python】浅谈enumerate 函数
enumerate 函数用于遍历序列中的元素以及它们的坐标: >>> for i,j in enumerate(('a','b','c')): print i,j 0 a 1 b ...
- 浅谈Oracle函数返回Table集合
在调用Oracle函数时为了让PL/SQL 函数返回数据的多个行,必须通过返回一个 REF CURSOR 或一个数据集合来完成.REF CURSOR 的这种情况局限于可以从查询中选择的数据,而整个集合 ...
- 浅谈JavaSccript函数与对象
函数 解剖函数 function One(leve1 , leve2){ //code return leve1+leve2 } 注释: 形参不需要加上类型: return语句为可选,没有return ...
随机推荐
- 动态规划:DAG-嵌套矩形
据说DAG是动态规划的基础,想一想还真的是这样的,动态规划的所有状态和转移都可以归约成DAG DAG有两个典型模型,一个是嵌套矩形问题一个是硬币问题,这里仅介绍一个嵌套矩形问题 等二轮复习的时候再补上 ...
- 「6月雅礼集训 2017 Day2」C
[题目大意] 有一棵n个点的完全二叉树,边权均为1,每个点有小鸟容量c[i] 依次来了m只小鸟,第i只小鸟初始位置在pos[i]上,问来了x只小鸟的时候,怎样安排小鸟的路线可以使得小鸟移动的边权和最小 ...
- 【POJ 1719】 Shooting Contest (二分图匹配)
题目链接 把每一列能射的两行和这一列连边,然后跑一边匈牙利就行了. #include <cstdio> #include <cstring> #include <algo ...
- 图像转换为二进制文件存入DSP6748
本文为原创作品,转载请注明出处 欢迎关注我的博客:http://blog.csdn.net/hit2015spring和http://www.cnblogs.com/xujianqing/ 这篇博客主 ...
- JAVA开发环境及其开发
成功安装之后,进行测试是否真的成功安装,点击[开始]----[运行]----输入 CMD,在命令提示符里面输入"Java -version"并按回车键,出现下图,即为安装成功. 选 ...
- SpringMVC与Spring的父子容器关系
问题: 在整合框架的时候有人也许会产生一个问题:能不能只配置一个扫描包加载实现类的扫描驱动,即在根目录下扫描所有的注解(@Controller.@Service.@Repository.@Compne ...
- 慎用Java递归调用
总结:慎用Java递归调用,测试时可以尝试该方法,否则尽量不要使用递归!递归过多调用时,最好改为for或者whlie来代替. 在java语言中,使用递归调用时,如果过多的调用容易造成java.lang ...
- centos7.3安装caffe出现错误:/bin/ld: cannot find -lcblas /bin/ld: cannot find -latlas
安装caffe时需要依赖库atlas,可使用yum -y install atlas-devel 安装,但是安装之后还是有可能出现错误: /bin/ld: cannot find -lcblas / ...
- HDU-3374
String Problem Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)To ...
- rest_framework 访问频率(节流)流程
访问频率流程 访问频率流程与认证流程非常相似,只是后续操作稍有不同 当用发出请求时 首先执行dispatch函数,当执行当第二部时: #2.处理版本信息 处理认证信息 处理权限信息 对用户的访问频率进 ...
