【原】Coursera—Andrew Ng机器学习—课程笔记 Lecture 5 Octave Tutorial—5.5 控制语句： for， while， if 语句

5.5 控制语句： for， while， if 语句

　　参考视频: 5 - 5 - Control Statements_ for, while, if statements (13 min).mkv

1、for 循环 通过 index 访问列向量

 >> v = zeros(,)
 v =

 >> for i =  : ,
      v(i) =  ^ i;
    end;
 >> v
 v =

2、for 循环 直接访问列向量元素

 >> indices =  : ;
 >> indices
 indices =

 >> for i = indices,
       disp(i);
    end;

3、while 循环访问列向量

 >> i = ;
 >> while i <= ,
       v(i) = ;
       i = i + ;
    end;
 >> v
 v =

4、while(true) 和 break

 >> i =  ;
 >> while(true),
      v(i) = ;
      i = i + ;
      if i == ,
         break;
      end;
    end;
 >>
 >> v
 v =

5、if else 语句

 >> v() = ;
 >> if v() == ,
       disp('The value is one');
    elseif v() == ,
       disp('The value is two');
    else,
       disp('The value is not one or two');
    end;
 The value is two

6、自定义函数 function

　　定义函数 squareThisNumber(x)，内容如下：　

 function y = squareThisNumber(x)
   y = x^;
 endfunction

　　将函数保存为squarethisnumber.m，注意此时是小写。

　　这时候调用函数 squareThisNumber(2) 提示找不到函数

 >> squareThisNumber();
 error: 'squareThisNumber' undefined near line  column
 >>
 >> ls
 [.]                         featuresX.dat               priceY.dat
 [..]                        hello.dat                   squarethisnumber.m

　　将文件命名为函数一致squareThisNumber.m（大小写也一致），这时候调用函数成功

 >> ls
 [.]                         featuresX.dat               priceY.dat
 [..]                        hello.dat                   squareThisNumber.m
 >> squareThisNumber();
 >> a = squareThisNumber();
 >> a
 a =  

　　这说明：Octave 是大小写敏感的，文件名必须和函数名大小写一致。

7、多个返回值的函数

　　Octave 函数有和其他语言不一样的地方是可以返回多个值。定义方法squareAndCubeThisNumber(x)如下：

 function [y1, y2] = squareAndCubeThisNumber(x),
   y1 = x ^ ;
   y2 = x ^ ;
 endfunction

　　调用：

 >> a = squareAndCubeThisNumber()　　% 接受了第一个返回值
 a =
 >> [a, b] = squareAndCubeThisNumber()　　% 接受两个返回值
 a =
 b =  

8、更复杂的函数

　　保存下面的函数到costFunctionJ.m中

 function J = costFunctionJ(X, y, theta),
   % X is the "design matrix" containing our training examples
   % y is the class labels

   m = size(X, );   % number of training examples, size of rows
   predictions = X * theta; % predictions of hapothesis on all m examples
   sqrErrors = (predictions - y) .^ ; % squared errors .^ 指的是对数据中每个元素平方

   J =  / ( * m) * sum(sqrErrors); 

 endfunction

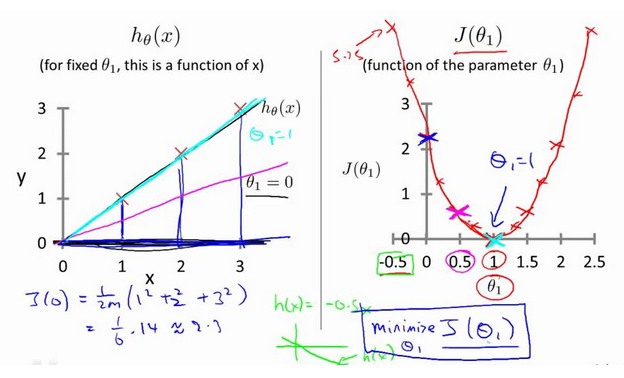
　　针对上边的数据集初始化矩阵。调用函数，计算代价函数的值。

 >> X = [ ;   ;  ];
 >> y = [;;];
 >> theta = [;];　　　　　　% Θ为0,1  h(x)=x  此时完全拟合数据，代价函数的值为0
 >> j = costFunctionJ(X,y,theta)
 j = 

 >> theta = [;];　　　　　 % Θ 为0,0 h(x)=0 此时不能拟合数据
 >> j = costFunctionJ(X,y,theta)
 j =  2.3333

 >> (^ + ^ + ^) / (*)　　% 代价函数的值
 ans =  2.3333