codeforce 985C Liebig's Barrels（贪心+思维）

Liebig's Barrels

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You have m = n·k wooden staves. The i-th stave has length ai. You have to assemble n barrels consisting of k staves each, you can use any k staves to construct a barrel. Each stave must belong to exactly one barrel.

Let volume vj of barrel j be equal to the length of the minimal stave in it.

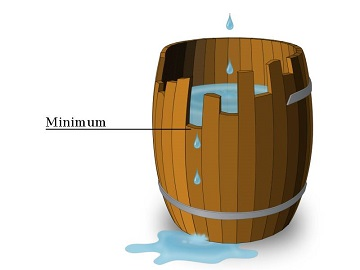
You want to assemble exactly n barrels with the maximal total sum of volumes. But you have to make them equal enough, so a difference between volumes of any pair of the resulting barrels must not exceed l, i.e. |vx - vy| ≤ l for any 1 ≤ x ≤ n and 1 ≤ y ≤ n.

Print maximal total sum of volumes of equal enough barrels or 0 if it's impossible to satisfy the condition above.

Input

The first line contains three space-separated integers n, k and l (1 ≤ n, k ≤ 105, 1 ≤ n·k ≤ 105, 0 ≤ l ≤ 109).

The second line contains m = n·k space-separated integers a1, a2, ..., am (1 ≤ ai ≤ 109) — lengths of staves.

Output

Print single integer — maximal total sum of the volumes of barrels or 0 if it's impossible to construct exactly n barrels satisfying the condition |vx - vy| ≤ l for any 1 ≤ x ≤ n and 1 ≤ y ≤ n.

Examples

input

Copy

4 2 1
2 2 1 2 3 2 2 3

output

Copy

7

input

Copy

2 1 0
10 10

output

Copy

20

input

Copy

1 2 1
5 2

output

Copy

2

input

Copy

3 2 1
1 2 3 4 5 6

output

Copy

0

Note

In the first example you can form the following barrels: [1, 2], [2, 2], [2, 3], [2, 3].

In the second example you can form the following barrels: [10], [10].

In the third example you can form the following barrels: [2, 5].

In the fourth example difference between volumes of barrels in any partition is at least 2 so it is impossible to make barrels equal enough.

题意：输入  n  k  l    你要做n个桶，每个桶需要k个木板，用木板拼好的桶相互之间体积的差距<=l，桶的体积大小就是最短的那根木板的长度大小。

第二行 共n*k个数，分别表示n*k个木板的长度。

分析：

先对边排个序

不存在的情况，就是a[n]-a[1]>l，那就是不存在，因为要是差距尽可能小，前n小的都分别作为n个桶的一块木板，那么这之中最大的差距就是a[n]-a[1]，要是a[n]-a[1]都满足条件（<=l）了，那就满足条件了。

其次，要使体积和最大输出体积和，我毛想想觉得s=a[1]+……a[n]，结果WA了，引起了我的深思。

因为：

eg：4    3    17

1   2   3   5   9   13    21  22  23  25 26

它可以这样组3组：

18  25  26

13   22  23

1     2     3

5     9   21

这样体积为1+5+13+18=37，不是简单地1 +2 +3 +5=11

所以我的思路：先要找到最大的满足条件的数，可以用二分找更快，在这组样例中，是18，它-a[1]<=l，

那么从最后开始去k-1个和18拼，s+=18，再下一个数13（25  26），再从最后找k-1个数（22  23），

再下一个数9，发现再k-1个数不够了，那就从头开始找了，（1   2   3）一组，在去（5   9  13）时，发现13

已经被取走，那就s+=5就可以了。

#include <iostream>
#include<cstring>
#include<string>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<deque>
#include<vector>
#define ll long long
#define inf 0x3f3f3f3f
#define mod 1000000007;
using namespace std;
ll a[];
bool cmp(ll a,ll b)
{
    return a<b;
}
int main()
{
    ll n,k,l;
    scanf("%I64d%I64d%I64d",&n,&k,&l);
    for(ll i=;i<=n*k;i++)
    {
        scanf("%I64d",&a[i]);
    }
    sort(a+,a++n*k,cmp);
    if(a[n]-a[]>l)
    {
        printf("");
    }
    else
    {
        ll s=;
        ll p=-;
        for(ll i=n*k;i>=;i--)
        {
            if(a[i]-a[]<=l)
            {
                p=i;//找到标准数，最大的满足条件的数
                break;
            }
        }
        s=;
        int num=;//记录从标准数向前取了多少
        int j=p;
        for(ll i=n*k;i-(k-)>p;i=i-(k-))//先从后往前取
        {
            s+=a[j--];
            num++;
        }
        for(ll i=;i<p-num+;i=i+k)//在从前往后取
        {
            s+=a[i];
        }
        printf("%I64d",s);
    }
    return ;
}