Python 堆与堆排序

堆排序与快速排序，归并排序一样都是时间复杂度为O(N*logN)的几种常见排序方法。学习堆排序前，先讲解下什么是数据结构中的二叉堆。

二叉堆的定义

二叉堆是完全二叉树或者是近似完全二叉树。

二叉堆满足二个特性：

1．父结点的键值总是大于或等于（小于或等于）任何一个子节点的键值。

2．每个结点的左子树和右子树都是一个二叉堆（都是最大堆或最小堆）。

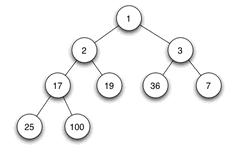
当父结点的键值总是大于或等于任何一个子节点的键值时为最大堆。当父结点的键值总是小于或等于任何一个子节点的键值时为最小堆。下图展示一个最小堆：

由于其它几种堆（二项式堆，斐波纳契堆等）用的较少，一般将二叉堆就简称为堆。

堆的存储

一般都用数组来表示堆，i结点的父结点下标就为(i – 1) / 2。它的左右子结点下标分别为2 * i + 1和2 * i + 2。如第0个结点左右子结点下标分别为1和2。

堆的操作——插入删除

下面先给出《数据结构C++语言描述》中最小堆的建立插入删除的图解，再给出本人的实现代码，最好是先看明白图后再去看代码。

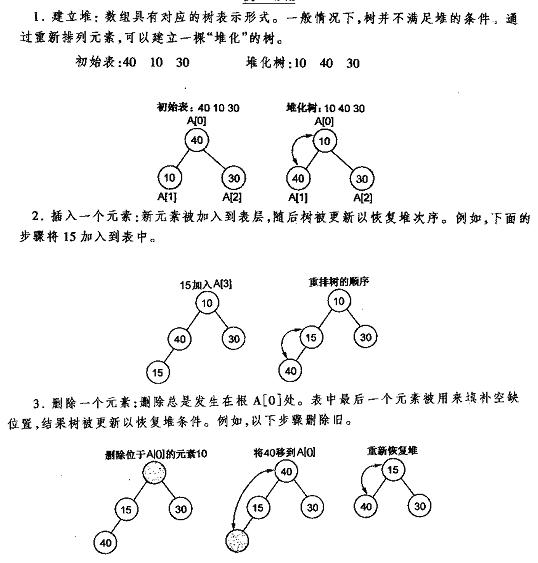
堆的插入

每次插入都是将新数据放在数组最后。可以发现从这个新数据的父结点到根结点必然为一个有序的数列，现在的任务是将这个新数据插入到这个有序数据中——这就类似于直接插入排序中将一个数据并入到有序区间中，对照《白话经典算法系列之二直接插入排序的三种实现》不难写出插入一个新数据时堆的调整代码：

更简短的表达为：

void MinHeapFixup(int a[], int i)

{

    for (int j = (i - ) / ; (j >=  && i != )&& a[i] > a[j]; i = j, j = (i - ) / )

        Swap(a[i], a[j]);

}

插入时：

//在最小堆中加入新的数据nNum

void MinHeapAddNumber(int a[], int n, int nNum)

{

    a[n] = nNum;

    MinHeapFixup(a, n);

}

堆的删除

按定义，堆中每次都只能删除第0个数据。为了便于重建堆，实际的操作是将最后一个数据的值赋给根结点，然后再从根结点开始进行一次从上向下的调整。调整时先在左右儿子结点中找最小的，如果父结点比这个最小的子结点还小说明不需要调整了，反之将父结点和它交换后再考虑后面的结点。相当于从根结点将一个数据的“下沉”过程。下面给出代码：

堆化数组

有了堆的插入和删除后，再考虑下如何对一个数据进行堆化操作。要一个一个的从数组中取出数据来建立堆吧，不用！先看一个数组，如下图：

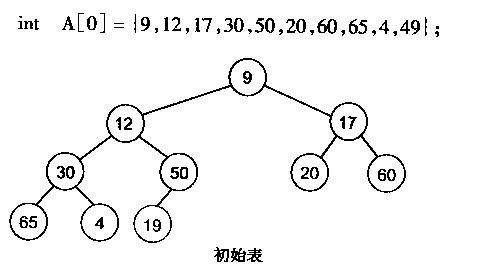
很明显，对叶子结点来说，可以认为它已经是一个合法的堆了即20，60， 65， 4， 49都分别是一个合法的堆。只要从A[4]=50开始向下调整就可以了。然后再取A[3]=30，A[2] = 17，A[1] = 12，A[0] = 9分别作一次向下调整操作就可以了。下图展示了这些步骤：

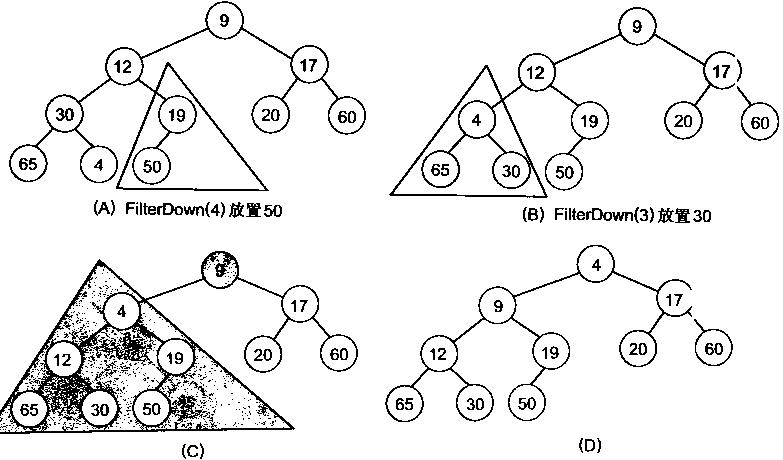
写出堆化数组的代码：

//建立最小堆

void MakeMinHeap(int a[], int n)

{

    for (int i = n /  - ; i >= ; i--)

        MinHeapFixdown(a, i, n);

}

至此，堆的操作就全部完成了(注1)，再来看下如何用堆这种数据结构来进行排序。

堆排序

首先可以看到堆建好之后堆中第0个数据是堆中最小的数据。取出这个数据再执行下堆的删除操作。这样堆中第0个数据又是堆中最小的数据，重复上述步骤直至堆中只有一个数据时就直接取出这个数据。

由于堆也是用数组模拟的，故堆化数组后，第一次将A[0]与A[n - 1]交换，再对A[0…n-2]重新恢复堆。第二次将A[0]与A[n – 2]交换，再对A[0…n - 3]重新恢复堆，重复这样的操作直到A[0]与A[1]交换。由于每次都是将最小的数据并入到后面的有序区间，故操作完成后整个数组就有序了。有点类似于直接选择排序。

void MinheapsortTodescendarray(int a[], int n)

{

    for (int i = n - ; i >= ; i--)

    {

        Swap(a[i], a[]);

        MinHeapFixdown(a, , i);

    }

}

注意使用最小堆排序后是递减数组，要得到递增数组，可以使用最大堆。

由于每次重新恢复堆的时间复杂度为O(logN)，共N - 1次重新恢复堆操作，再加上前面建立堆时N / 2次向下调整，每次调整时间复杂度也为O(logN)。二次操作时间相加还是O(N * logN)。故堆排序的时间复杂度为O(N * logN)。STL也实现了堆的相关函数，可以参阅《STL系列之四 heap 堆》。

注1 作为一个数据结构，最好用类将其数据和方法封装起来，这样即便于操作，也便于理解。此外，除了堆排序要使用堆，另外还有很多场合可以使用堆来方便和高效的处理数据，以后会一一介绍。

转载请标明出处，原文地址：http://blog.csdn.net/morewindows/article/details/6709644